7.4 Трубы и их соединения

Техника транспорта теплоты предъявляет следующие основные требования к трубам, применяемым для теплопроводов:

1) достаточная механическая прочность и герметичность при имеющих место давлениях и температурах теплоносителя;

2) эластичность и стойкость против термических напряжений при переменном тепловом режиме;

3) постоянство механических свойств;

4) стойкость против внешней и внутренней коррозии;

5) малая шероховатость внутренних поверхностей;

6) отсутствие эрозии внутренних поверхностей;

7) малый коэффициент температурных деформаций;

8) высокие теплоизолирующие свойства стенок трубы;

9) простота, надежность и герметичность соединения отдельных элементов;

10) простота хранения, транспортировки и монтажа.

Все известные до настоящего времени типы труб одновременно не удовлетворяют всем перечисленным требованиям. В частности, этим требованиям не вполне удовлетворяют стальные трубы, применяемые для транспорта пара и горячей воды. Однако высокие механические свойства и эластичность стальных труб, а также простота, надежность и герметичность соединений (сварка) обеспечили практически 100 %-ное применение этих труб в системах централизованного теплоснабжения.

Труба, рассчитанная на какое-либо условное давление р_у, может быть применена для рабочего давления

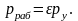(7.1)

Значения коэффициента ε в зависимости от температуры транспортируемой среды приведены в таблице 7.1.

Таблица 7.1. Значения коэффициента ε в зависимости от температуры транспортируемой среды

Наибольшая температура среды, оС	200	250	300	350	400	425	435	445
Коэффициент ε	1,0	0,9	0,8	0,7	0,64	0,53	0,5	0,45

Пробное давление для гидравлических испытаний трубопроводов определяется по формуле

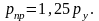(7.2)

Основные типы стальных труб, применяемых для ТС:

диаметром до 400 мм включительно – бесшовные, горячекатаные;

диаметром выше 400 мм – электросварные с продольным швом и электросварные со спиральным швом.

Трубы для ТС изготавливаются главным образом из стали следующих марок: Ст2сп, Ст3сп, стали 10, 20, 10Г2, 15ГС, 16ГС, 17ГС.

На рисунке 7.24 показан участок трубопровода. Под действием внутреннего давления в элементе стенки трубопровода возникают следующие напряжения:

1) напряжение растяжения σ₁ в торцевой плоскости, нормальной к оси трубы; его вектор направлен по образующей цилиндра;

2) напряжение растяжения σ₂ в осевой (меридиональной) плоскости; его вектор направлен по касательной к окружности трубы;

3) напряжение сжатия σ₃, нормальное к внутренней поверхности трубы.

Кроме того, в стенках трубопроводов возникают напряжения изгиба:

σ₄ – под действием собственного веса трубопровода, веса тепловой изоляции и веса теплоносителя. В надземных теплопроводах возможен также изгиб под действием скоростного напора ветра;

σ₅ – под действием термической деформации в гнутых компенсаторах и на участках естественной компенсации.

Рисунок 7.24 Схема напряжений в стенках трубопровода под действием внутреннего давления.

Перейдем к расчету усилий и напряжений, действующих в трубопроводах ТС.

Введем следующие условные обозначения:

р – внутреннее давление в трубопроводе, Па; Р – осевая сила, Н; М – изгибающий момент, Н·м (1 Н·м = 10,2 кгс · см); М_к – крутящий момент, Н·м; d_н – наружный диаметр трубы, м; d_в – внутренний диаметр трубы, м; δ – толщина стенки трубы, м; f_т = π (d_в + δ) δ – площадь торцевого сечения трубы, м² ; Е – модуль продольной упругости, для стали Е= 19,6 · 10¹⁰ Па; G – модуль сдвига, для стали G = 7,85 · 10¹⁰ Па; J = 0,05 ( d_н⁴ – d_в⁴ ) – экваториальный момент инерции трубы, м⁴; W = 0,1 ( d_н⁴ – d_в⁴ ) / d_н – экваториальный момент сопротивления трубы, м ; J_п = 0,1 ( d_н⁴ – d_в⁴ ) – полярный момент инерции трубы, м⁴; W_п = 0,2 ( d_н⁴ – d_в⁴ ) / d_н – полярный момент сопротивления трубы, м³ ; σ – напряжение, Па.

При одновременном действии всех видов деформации – при растяжении, изгибе и кручении – приведенное максимальное напряжение

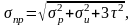
(7.3)

где σ_р – суммарное напряжение растяжения от внутреннего давления;

σ_и – суммарное напряжение от изгиба.

П риведенное напряжение не должно превосходить допускаемое для наиболее опасного сечения трубопровода, которым является сварной стык. Следовательно

(7.4)

где [σ] – допускаемое напряжение; φ – коэффициент прочности сварного стыка.

Напряжение растяжения в трубопроводе под действием внутреннего давления определяется следующим образом. Осевая сила внутреннего давления, действующая в торцевой плоскости, нормальной к оси трубы

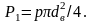
(7.5)

Напряжение растяжения в торцевой плоскости с вектором, направленным по образующей цилиндра

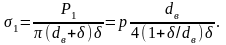
(7.6)

Значение δ/d_в в ТС изменяется от 0,05 для трубопроводов малого диаметра (d_в = 50 мм) до 0,01 для трубопроводов большого диаметра (d_в = 1400 мм). Пренебрегая δ/d_в вследствие его малости по сравнению с 1, можно расчетное выражение для определения σ₁ записать в следующем виде

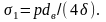
(7.6а)

Напряжение растяжения в осевой плоскости с вектором, направленным по дуге окружности, может быть определено по следующей формуле, составленной для участка трубы длиной l:

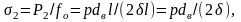
(7.7)

где Р₂ = рd_вl – сила внутреннего давления, действующая в осевой плоскости; f_o – площадь сечения стенок трубы в осевой плоскости: f_o = 2δl.

Напряжение сжатия δ₃ = р значительно меньше напряжений δ₁ и δ₂. Поэтому при расчете трубопроводов ТС величиной δ₃ обычно пренебрегают.

Суммарное напряжение от растяжения под действием внутреннего давления определяется по энергетической теории прочности

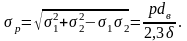
(7.8)

Для участков, на которых Р₁ = 0, а следовательно, δ₁ = 0

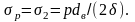
(7.8а)

Из сравнения (7.8) и (7.8а) видно, что в трубопроводах, испытывающих осевую силу внутреннего давления, напряжения в стенке δ_р на 15 % меньше, чем в трубопроводах, где эта сила не действует. Такой на первый взгляд парадоксальный вывод объясняется тем, что потенциальная энергия деформации формы, являющаяся по энергетической теории мерой прочности материала, получается меньше, когда напряжение растяжения действует в двух взаимно перпендикулярных плоскостях, а не в одной плоскости.

Формулы (7.5) – (7.8) относятся к условиям, при которых давление в трубопроводе постепенно возрастает от 0 до р.

В некоторых случаях, например при гидравлическом ударе, давление

в трубопроводе возрастает на величину р_у, практически мгновенно.

Возникающие при этом напряжения в трубопроводе вдвое больше, чем при постепенном повышении давления. Это объясняется тем, что при мгновенном возникновении нагрузки потенциальная энергия деформации вдвое больше, чем при постепенном повышении нагрузки.

Если до гидравлического удара давление в трубопроводе было равно р_н и в результате гидравлического удара давление повысилось на р_у то при расчете напряжений в трубопроводе на растяжение по формулам (7.5) – (7.8) следует принимать расчетное давление в трубопроводе

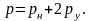
(7.9)

Суммарное напряжение от изгиба

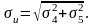
(7.10)

Крутящие моменты возникают только в пространственных трубопроводах. В плоскостных трубопроводах крутящие моменты равны нулю.

В этом случае приведенное максимальное напряжение

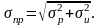
(7.11)

Так как σ_пр < σ_р + σ_и, из формулы (7.11), следует, что приведенное напряжение при одновременном действии растяжения и изгиба меньше арифметической суммы напряжений, возникающих в трубопроводе при раздельном действии этих деформаций.