2.2.2. Логические функции одной переменной

Существует четыре функции от одной логической переменной, т. к. согласно формуле (2.3) .

Таблица 2.2
x	f1	f2	f3	f4
0	0	0	1	1
1	0	1	0	1

Таблицы истинности всех четырёх функций одной переменной представлены в табл. 2.2.

Названия этих функций следующие: f₁ = 0 – нуль, f₂ = x – тождественная функция, f₃ = – логические отрицание (инверсия, функция НЕ), f₄ = 1 – единица. Как видно, для функций-констант f₁ и f₄ переменная x является фиктивной, а для функций f₂ и f₃ – существенной.

Три из приведённых выше функций являются тривиальными (константы “0” и “1”, а также тождественная функция); только последняя функция НЕ является нетривиальной.

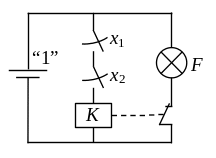
На рис. 2.1 с помощью батарейки, генерирующей константу “1”, ключа x и лампочки F объясняется смысл тождественной функции и отрицания НЕ.

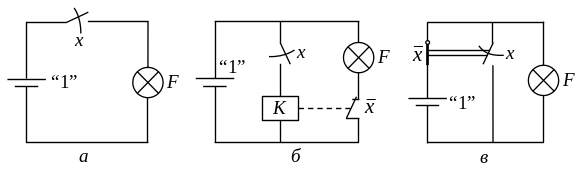Рис. 2.1. Пояснение смысла тождественной функции (а) и отрицания НЕ (б, в)

Из рис. 2.1, а видно, что когда ключ разомкнут (x = 0), цепь также разомкнута и лампочка не горит (F = 0); при замыкании ключа (x = 1) цепь замыкается, по ней начинает протекать ток и лампочка загорается (F = 1).

Иллюстрация операции НЕ требует небольшого усложнения схемы. В схеме на рис. 2.1, б использовано реле K. При разомкнутом ключе x (x = 0) реле выключено и управляемый им ключ замкнут, поэтому лампочка горит (F = 1). При замыкании ключа x (x = 1) реле срабатывает и размыкает ключ , из-за чего цепь лампочки разрывается, и она не будет гореть (F = 0).

Более простое объяснение смысла операции НЕ показано на рис. 2.1, в, где используется пара связанных ключей. При разомкнутом ключе x (x = 0) ключ наоборот замкнут, и лампочка горит (F = 1). При замыкании ключа x (x = 1) ключ размыкается, поэтому лампочка перестаёт гореть (F = 0).

2.2.3. Логические функции двух, трёх и более переменных

Количество функций двух переменных , а для трёх переменных имеем уже функций.

Таблицы истинности всех шестнадцати булевых функций двух переменных представлены в табл. 2.3.

Таблица 2.3

x1	x2	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15	f16
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Фиктивные переменные		x1 x2			x2		x1					x1		x2			x1 x2

Для каждой функции в четырёх строках таблицы приведены её значения, соответствующие четырём возможным комбинациям аргументов x₁ и x₂ . В таблице для каждой функции показаны также фиктивные переменные, если они имеются.

Функция f₁ называется нулём, а f₁₆ – единицей, как и в случае функций одной переменной. Функции f₄ , f₆ , f₁₁ и f₁₃ не зависят от одного из аргументов: , , , . Для функций f₄  и f₁₃ переменная x₁ является существенной, а x₂ – несущественной; для функций f₆  и f₁₁ ­– всё наоборот.

Только оставшиеся десять функций являются полноценными нетривиальными функциями двух переменных.

Табл. 2.3 можно представить и в другом виде, выполнив её транспонирование, результатом чего является табл. 2.4, где в последнем столбце указаны также обозначения соответствующих логических операций.

Рассмотрим подробнее все нетривиальные функции двух переменных, а для некоторых из них и функции трёх аргументов. Для функций двух переменных дополнительно проведены иллюстрации, поясняющие смысл соответствующих логических операций.

Таблица 2.4

Функция	х1 х2				Обозначения функций
	00	01	10	11
f1	0	0	0	0	“0”
f2	0	0	0	1
f3	0	0	1	0
f4	0	0	1	1	x1
f5	0	1	0	0
f6	0	1	0	1	x2
f7	0	1	1	0
f8	0	1	1	1
f9	1	0	0	0
f10	1	0	0	1
f11	1	0	1	0
f12	1	0	1	1
f13	1	1	0	0
f14	1	1	0	1
f15	1	1	1	0
f16	1	1	1	1	“1”

Функция f₂(x₁, x₂) = или или или называется конъюнкцией, логическим умножением или функцией И. Она принимает значение 1 только в том случае, когда все аргументы равны 1 (и x₁ = 1, и x₂ = 1), а значение 0 ­– во всех остальных случаях (когда хотя бы одна из переменных будет равна 0).

		x1	x2	F		x1	x2	x3	F
		0	0	0		0	0	0	0
		0	1	0		0	0	1	0
		1	0	0		0	1	0	0
		1	1	1		0	1	1	0
						1	0	0	0
						1	0	1	0
						1	1	0	0
						1	1	1	1

Рис. 2.2. Логическая функция И

На рис. 2.2 поясняется смысл операции И. Видно, что по цепи потечёт ток и лампочка загорится (F = 1) только тогда, когда замкнуты оба ключа (и x₁ = 1, и x₂ = 1).

Функция И трёх и более переменных также принимает значение “1” только при единичных значениях всех её аргументов (и x₁ = 1, и x₂ = 1, и x₃ = 1). Таблица истинности функции И имеет только одну “1” на последней комбинации.

Функция f₈(x₁, x₂) = или называется дизъюнкцией, логическим сложением или функцией ИЛИ. Она принимает значение 1, если хотя бы один из аргументов или все равны 1 (или x₁ = 1, или x₂ = 1, или x₁ = x₂ = 1), а значение 0 – только при x₁ = x₂ = 0. Из рис. 2.3 видно, что по цепи лампочки потечёт ток и она загорится тогда, когда замкнут хотя бы один из ключей.

		x1	x2	F		x1	x2	x3	F
		0	0	0		0	0	0	0
		0	1	1		0	0	1	1
		1	0	1		0	1	0	1
		1	1	1		0	1	1	1
						1	0	0	1
						1	0	1	1
						1	1	0	1
						1	1	1	1

Рис. 2.3. Логическая функция ИЛИ

Функция ИЛИ трёх и более переменных также принимает значение “1” при единичном значении любого из аргументов (или x₁ = 1, или x₂ = 1, или x₃ = 1, или x₁ = x₂ = x₃ = 1). Таблица истинности функции ИЛИ имеет только один “0” на первой комбинации.

Функция f₁₅(x₁,x₂) = или или или или называется штрихом Шеффера, функцией Шеффера или функцией И-НЕ. Она работает полностью противоположно операции И, поэтому принимает значение 0 только в том случае, когда все аргументы равны 1 (и x₁ = 1, и x₂ = 1), а значение 1 – в остальных случаях, т. е. когда хотя бы один из аргументов равен 0.

На рис. 2.4 поясняется смысл операции И-НЕ. Видно, что в цепи лампочки не будет течь ток и она не будет гореть (F = 0) только тогда, когда оба ключа замкнуты (и x₁ = 1, и x₂ = 1), т. к. при этом реле K срабатывает и размыкает свой ключ. Если же разомкнут хотя бы один из ключей (или x₁ = 0, или x₂ = 0, или x₁ = x₂ = 0), то реле не размыкает ключ в цепи лампочки и она горит (F = 1).

		x1	x2	F		x1	x2	x3	F
		0	0	1		0	0	0	1
		0	1	1		0	0	1	1
		1	0	1		0	1	0	1
		1	1	0		0	1	1	1
						1	0	0	1
						1	0	1	1
						1	1	0	1
						1	1	1	0

Рис. 2.4. Логическая функция И-НЕ

Функция И-НЕ трёх и более переменных также принимает значение “0” только при единичных значениях всех её аргументов (и x₁ = 1, и x₂ = 1, и x₃ = 1). Вообще таблица истинности функции И-НЕ имеет только один “0” на последней комбинации.

Функция f₉(x₁,x₂) = или или называется функцией Пирса, стрелкой Пирса, а также функцией ИЛИ-НЕ. Она принимает значение 0, если хотя бы один из аргументов или все равны 1 (или x₁ = 1, или x₂ = 1, или x₁ = x₂ = 1), а значение 1 – только при x₁ = x₂ = 0. Из рис. 2.5 видно, что в цепи лампочки не будет течь ток и она не будет гореть (F = 0), если замкнут хотя бы

		x1	x2	F		x1	x2	x3	F
		0	0	1		0	0	0	1
		0	1	0		0	0	1	0
		1	0	0		0	1	0	0
		1	1	0		0	1	1	0
						1	0	0	0
						1	0	1	0
						1	1	0	0
						1	1	1	0

Рис. 2.5. Логическая функция ИЛИ-НЕ

один из ключей (или x₁ = 1, или x₂ = 1, или x₁ = x₂ = 1), т. к. при этом реле K срабатывает и размыкает свой ключ. Если же оба ключа разомкнуты (и x₁ = 0, и x₂ = 0), то реле не размыкает ключ в цепи лампочки и она горит (F = 1).

Функция ИЛИ-НЕ трёх и более переменных также принимает значение “0” при единичном значении любого из аргументов (или x₁ = 1, или x₂ = 1, или x₃ = 1, или x₁ = x₂ = x₃ = 1). Таблица истинности функции ИЛИ имеет только одну “1” на первой комбинации.

Функция f₇(x₁,x₂) = называется функцией сложения по модулю 2, а также исключающим ИЛИ, кольцевой суммой, нетождественностью, неэквивалентностью, нечётностью. Значения этой функции получаются по правилу суммы по модулю 2: 0  0 = 0, 0  1 = 1, 1  0 = 1, 1  1 = 0. Она принимает значение 1, когда только один из аргументов равен 1 (или только x₁ = 1, или только x₂ = 1) или когда сумма значений аргументов является нечётным числом, исключая тем самым одинаковые значения аргументов, т. к. при равных значениях переменных функция принимает значение 0.

		x1	x2	F		x1	x2	x3	F
		0	0	0		0	0	0	0
		0	1	1		0	0	1	1
		1	0	1		0	1	0	1
		1	1	0		0	1	1	0
						1	0	0	1
						1	0	1	0
						1	1	0	0
						1	1	1	1

Рис. 2.6. Логическая функция Исключающее ИЛИ

Из рис. 2.6 видно, что в цепи лампочки будет течь ток и она будет гореть (F = 1) только тогда, когда переменные x₁ и x₂ будут иметь различные значения (только в этом случае лампочка будет подключена к батарее). При одинаковых значениях переменных лампочка будет замыкаться сама на себя и не будет гореть (F = 0).

Для трёх и более переменных такая функция будет иметь смысл только функции суммы по модулю 2 (кольцевой суммы) и нечётности. Например, значение функции будет равно 1, если сумма всех значений аргументов есть нечётное число, и 0 – если эта сумма является чётным числом.

Функция f₁₀(x₁,x₂) = или или показывает равнозначность (эквивалентность, тождественность) аргументов x₁, x₂ . Она также называется функцией чётности. Эта функция принимает значение 1, только когда оба аргумента равны между собой (или x₁ = x₂ = 0, или x₁ = x₂ = 1) или когда сумма значений аргументов является чётным числом, поэтому можно сделать вывод, что она является обратной функцией для исключающего ИЛИ.

		x1	x2	F		x1	x2	X3	F
		0	0	1		0	0	0	1
		0	1	0		0	0	1	0
		1	0	0		0	1	0	0
		1	1	1		0	1	1	1
						1	0	0	0
						1	0	1	1
						1	1	0	1
						1	1	1	0

Рис. 2.7. Логическая функция равнозначности (чётности)

Для получения схемы функции равнозначности (чётности) можно на схеме на рис. 2.6 поменять местами контакты любой из переменной, но только одной: либо для x₁ , либо для x₂ .

Из рис. 2.7 видно, что в цепи лампочки будет течь ток и она будет гореть (F = 1) только тогда, когда переменные x₁ и x₂ будут иметь одинаковые значения, т. к. только в этом случае лампочка будет подключена к батарее. При разных значениях переменных лампочка будет замыкаться сама на себя и не будет гореть (F = 0).

Для трёх и более переменных такая функция будет иметь смысл только функции чётности. Например, значение функции будет равно 1, если сумма всех значений аргументов есть чётное число, и 0 – если эта сумма – нечётное число.

Функция f₁₂(x₁, x₂) = или – функция следования (импликация) от x₂ к x₁ , которая принимает значение 0 тогда и только тогда, когда x₁ = 0, а x₂ = 1.

Функция f₁₄(x₁,  x₂) = или – функция следования (импликация) от x₁ к x₂ , принимающая значение 0 тогда и только тогда, когда x₁ = 1, а x₂ = 0.

В табл. 2.5 и 2.6 отражены таблицы истинности этих двух функций-импликаций, которые имеют смысл только для двух аргументов.

Таблица 2.5 Таблица 2.6

x1	x2	F		x1	x2	F
0	0	1		0	0	1
0	1	0		0	1	1
1	0	1		1	0	0
1	1	1		1	1	1

Импликация Импликация

Функция f₃(x₁,x₂) = или или или называется функцией запрета по x₂ и характеризуется тем, что равенство x₂ = 1 запрещает функции принимать значение “1” при любых значениях аргумента x₁ , обнуляя тем самым функцию.

Функция f₅(x₁,x₂) = или или или называется функцией запрета по x₁ , т. к. равенство x₁ = 1 запрещает функции принимать значение “1” при любых значениях аргумента x₂ .

Таблица 2.7 Таблица 2.8

x1	x2	F		x1	x2	F
0	0	0		0	0	0
0	1	0		0	1	1
1	0	1		1	0	0
1	1	0		1	1	0

Функция запрета по x₂ Функция запрета по x₁

Эти две функции запрета, таблицы истинности которых приведены в табл. 2.7 и 2.8, также существуют только для случая двух переменных.

Теоретически, функции И, ИЛИ, И-НЕ, ИЛИ-НЕ, чётность и нечётность могут иметь сколько угодно, но конечное число аргументов x₁, x₂, …, x_m .