Лекция 4. Изопроцессы. Работа и теплоемкость в политропических процессах. Уравнение Ван-дер-Ваальса

Адиабатический процесс – это процесс, происходящий без теплообмена с окружающей средой. Поэтому первое начало термодинамики (7) для него будет выглядеть так: . Подставим U из (16):

, или , 

, 

.

Разделим последнее выражение на ,  , и преобразуем, 

.

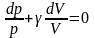Левая часть – это сумма дифференциалов логарифмов, 

,  , 

. (17)

Э то и есть уравнение адиабаты, называемое еще уравнением Пуассона. Пользуясь уравнением состояния, уравнение адиабаты можно представить в другом виде:

.

В адиабатическом процессе молярная теплоемкость равна нулю, т.к. нет теплообмена. Из урав-

82

нения видно, что >1, поэтому адиабата (кривая 2 на рис.6) идет круче изотермы (pV=const, кривая 1).

Политропические процессы. Так называются процессы, уравнение которых имеет вид:

, (18)

где n - любое число. Из этого определения следует, что адиабатический процесс является политропическим с показателем политропы n = . Политропическими являются также изохорический ( = ), изобарический (р= ) и изотермический (Т = ) процессы. Покажем, что в любом политропическом процессе молярная теплоемкость постоянна: . Запишем по аналогии с адиабатическим процессом уравнение политропы (18) в форме

и вычислим от него полный дифференциал:

, 

, 

 (14), 

= . 

. (19)

Подстановка в эту формулу значения n =1,  =1 (для изотермического процесса) дает ; 83

для адиабатического процесса n =  , откуда ; для процессов: изохорического ; для изобарического . Из (19) после подстановки и можно выразить показатель политропы через теплоемкости:

. (20)

Работа газа при политропических процессах. В принципе работу газа в любом процессе принципиально можно вычислить по формуле (9). Однако во многих случаях работу удобнее вычислить с помощью I начала термодинамики:

= = .

Подставляя сюда (см. выше (19)), получим

= .

Мы получили еще две формулы для работы в любом политропическом процессе:

. (21)

Последняя формула неудобна только для изотермических процессов, для которых вычислим работу непосредственно из (9). Подставим в (9) давление из уравнения состояния: :

.

Таким образом, в изотермическом процессе при температуре Т и изменении объема от V₁ до V₂ совершается работа

84

. (22)

Внутренняя энергия и теплоемкость. Внутреннюю энергию можно выразить через число степеней свободы, если принять во внимание, что внутренняя энергия одного моля – это средняя энергия молекулы (5), умноженная на число Авогадро:

. (23)

С учетом (12) и (15) получим

; . (24)

Полученные выражения позволяют придать ещё один смысл постоянной адиабаты:

. (25)

Уравнение Ван-дер-Ваальса. Модель идеального газа имеет область применения, ограниченную не слишком большими давлениями. По мере роста давления наблюдаются все большие отклонения от уравнения . Выделим две причины такого поведения.

1. Молекулы имеют собственный объем, который уже при 100 атм составляет более половины объема газа.

2. Взаимодействие между молекулами становится существенным: типичная кривая энергии взаимодействия между двумя молекулами в зависимости

85

от расстояния между ними приведена на рис.7. При r < молекулы отталкиваются, при r > притягиваются. Значит, по мере сближения молекул количественно и качественно меняется характер взаимодействия между ними.

Это влияние можно учесть, введя поправки в уравнение состояния для идеальных газов, и тогда получится уравнение Ван-дер-Ваальса, которое принято записывать для одного моля:

. (26)

Постоянные Ван-дер-Ваальса: а и b имеют для каждого газа свои значения. Поправка в первой скобке, , обусловлена силами притяжения между молекулами: при переходе к реальному газу давление на стенки сосуда уменьшается, его приходится искусственно «исправлять». Поправка b связана с уменьшением свободного объема за счет собственного объема молекул.