Молекулярная физика Лекция 1. Основное уравнение молекулярно-кинетической теории идеального газа

Молекулярная физика – это часть курса общей физики, в которой изучают свойства систем, исходя из молекулярно-кинетической теории. Согласно этой теории все тела состоят из огромного количества молекул (или атомов), находящихся в непрерывном хаотическом тепловом движении. Поведение систем, состоящих из очень большого количества частиц (макросистем), описываются с помощью вероятностных методов, позволяющих перейти к параметрам, характеризующим макроскопические свойства, исходя из коллективного поведения составляющих системы частиц и на основе молекулярно-кинетической теории. Термодинамический подход, когда система описывается параметрами состояния (объем, давление, температура и.т.д.) и статистический подход, говорящий на языке функций распределения и средних значений величин, взаимно дополняют друг друга. Молекулярно-кинетическая теория достигла особенно больших успехов применительно к газам.

Давление газа на стенки сосуда. Основное уравнение кинетической теории газов. Будем считать молекулы газа одинаковыми упругими шариками, которые большую часть времени не взаимодействуют друг с другом. Кратковременные взаимодействия сводятся к столкновениям, происходящим по законам упругого удара. Эта модель называется идеальным газом. На первом этапе будем считать, что молекулы пробегают от одной стенки сосуда до другой прямолинейно, перпендикулярно стенке и без столкновений между собой. Определим давление как модуль средней силы, действующей нормально к поверхности, отнесенный к площади этой поверхности:

.

71

Пусть газ находится в сосуде кубической формы с ребром l (рис.1). Молекула массы m, движущаяся со скоростью к левой стенке, при упругом соударении со стенкой получит приращение проекции импульса , затем отразится от правой стенки и полетит обратно. Время τ между двумя последовательными соударениями с левой стенкой τ= . За время Δt число соударений о левую стенку равно

= ,

а приращение импульса равно

= .

Пусть n₁ молекул в единице объема движутся со скоростью , n₂ молекул движутся со скоростью 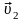, и т.д. Очевидно, что из n₁ молекул одна треть, т.е. молекул, движутся вдоль оси х, и по стольку же вдоль осей y и z. Всего молекул, движущихся в одном из трех направлений, будет , где - объем сосуда. За время Δt вследствие столкновений с левой стенкой эти молекулы получат суммарное приращение проекции импульса, равное

= .

По второму закону Ньютона ,  давление на левую стенку со стороны этих молекул равно

72

= , 

.

Аналогично молекул (со скоростями ) создадут давление и т.д. Давление, производимое всеми молекулами на левую стенку равно:

+ +…+ = = .

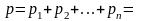Последняя сумма представляет собой сумму квадратов всех скоростей в единице объема. Разделив её на концентрацию n ( ), мы получим средний квадрат скорости:

.

Поэтому давление = . Перепишем это уравнение

, 

. (1)

Это и есть основное уравнение кинетической теории газов: давление газа равно двум третям средней кинетической энергии поступательного движения молекул в единице объема газа.

73

Лекция 2. Уравнение состояния идеального газа.