4. Полные и неполные нормированные пространства.

Пусть Х- нормированное пространство с нормой || . || счётное, упорядоченное мн-во элементов {Xn}от 1 и до ∞, или {Xn}будем называть последовательностью если выбраны некоторые члены последовательности {Xnk}то получим последовательность, называющуюся подпоследовательностью.

Понятие нормы(а значит и метрики)позволяет определить сходимость последовательности, как известно из анализа, если численная последовательность удовлетворяет условию Коши, то она сходится(критерии сходимости), однако в ФАНе эти понятия разделяются.

Опр 4.1 Последовательность {хn}Є х сходящаяся к элементу хo Є Х (хn→ хo при n→ ∞),если || хn- хo ||→0 при n→ ∞ bn = || хn- хo ||.

Данное определение принимается за основное и допускает эквивалентную переформулировку:

При любом ε>0 сущ-ет N=N(ε) такой что u >= N для всех элементов || хn- хo || < ε для сход-ся послед-ей норм. пр-ва сост.основным аналогом о сходимости:

1)если последовательность сх-ся то предельный элемент один.

2)если последовательность сх-ся то любая её последовательность сх-ся к этому же элементу.

3)над сх-ся последовательностью можно производить элементарные алгебр.действия.

(хn→хo и уn →уo ≥ хn± уn ; λn→λ и хn→хo, то λn* хn→λo* хo)

Опр 4.2 Посл-сть {хn} фундаментальная если для любого произв.фикс. р || хn+р- хo ||→0.

Р! След. нерав-во || хn+р- хo || = || (хn+р- хo)+( хo - хn )||≤ || хn+р- хo ||+|| хn- хo ||.

Из сходимости следует фундаментальность, обратное- не верно.

Опр 4.3 Пусть пространство Х такое, что в нём любая фунд. посл-ть сх-ся к элементу данного пространства, тогда пр-во полное или Банаховое.

Банохово пр-во обладает рядом свойств классического нормированного пространства. Для известных норм. пр-в, норма определяет определённый вид сходимости , который можно охарактеризовать в терминах данного пространства.

Rn-линейное пр-во x=(x1,x2…xn) относительно любых из след. норм:

1. || х ||1=| x1|+ | x2|+…+| xn|=Σ(от i=1 до n) |xi|.

2. || х ||2=( Σ(от i=1 до n) |xi| 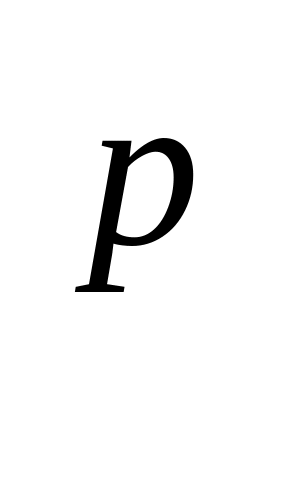) 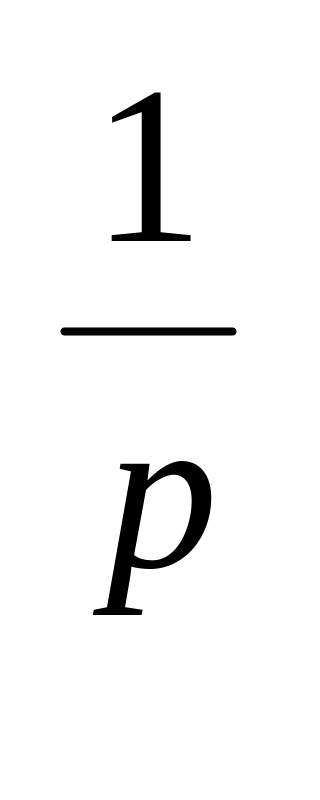,1<p<∞

3. || х ||3=max{| x1|+ | x2|+…+| xn|}=max|xi|

Примеры неполного норм.пр-ва.

Для построения примера неполного пр-ва достаточно на полн. пр-ве определить норму и в полученой норм. пр-ве доказать существование хотя бы 1 послед-ти, которая явл. фундаментальной по этой норме не сх-ся к элементам этого пространства,в качестве лин-го пр-ва фун-ии и для определённостей.

Пространство С[-1;1] с нормой || х ||= является не полным нормированным пространством.

5. Сравнение норм нормированных пространств.

Если на одном пр-ве Х рассматривается разные нормы, то получим нормы пространства разные, тогда возникают 2 ситуации интересные для анализа:

1)когда утверждение справедливо для 1 нормы можно переносить для пространства с другой нормой.

2)если ситуация 1) – не возможна, то как сравнивать 2 нормы с точки зрения более сильной сходимости, чья сходимость сильнее?

Опр 5.1 нормы || . ||1 и || . ||2 называются эквивалентыми(~), если существкет С1,С2 (const)≥0 такие что, С1*|| х ||1≤|| х ||2≤ С2*|| х ||1 (1)

Пусть 2 нормы ~ и рассмотрим некоторую послед-ть пр-ва Х.

Утв. Если 2 нормы пр-ва X ~, то порожденные ими сх-ти взаимозаменяемые,в частности если пространства полные по 1-й норме,то они ~ по 2-й.

То в понятии эквивалентности норм, может оказаться полезным для док-ва полноты пр-ва,если этот факт оказывается для более простых норм то полнота пр-ва сохр.для любой ~ формы.

Вывод: max-норма не может быть ~ интегральной нормой пр-ва С[a;b]

Св-ва отношения ~ :

1. || . ||~|| . ||

2. Если || . ||1~|| . ||2, то || . ||2~|| . ||3

3. ||.||1~||.||2 и ||.||2~||.||3 => ||.||1~||.||3

Более того нормы пр-ва Rn ~меж собой. Любые 2 нормы конечномерного пр-ва ~ меж собой.

Если 2 нормы не ~ то может быть выполнение: || х ||1≤С|| х ||2, х Є Х из выполнения сх-ти 2-й нормы→фундаментальность 1-й нормы,обратное неверно; выполнение неравенства доказывает что 2-я норма сильнее 1-й.

Max норма сильнее интегральной, из равной сходимости посл-ти непрерыв. ф-ий→ интегральная сх-ть в среднем и обратное неверно.

6. Открытые множества и замкнутые множества.

ОТКРЫТЫЕ МНОЖЕСТВА.

Назовем открытым ( замкнутым ) шаром с центром в точке а и радиусом r множество элементов х метрического пространства Х, удовлетворяющих, соответственно, условиям:

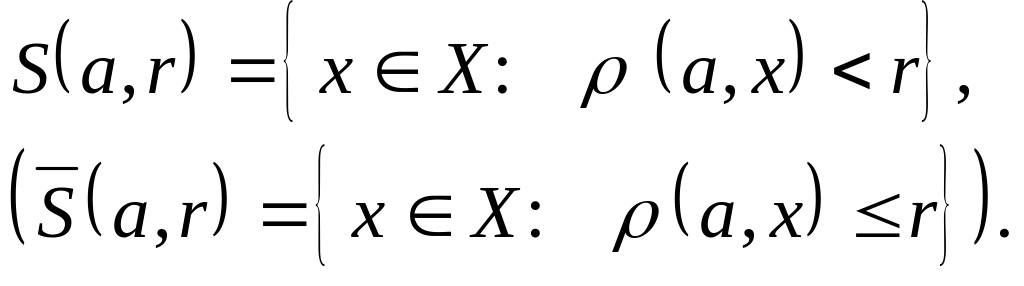
Примеры: 1. В ( на числовой оси ) :

2. В С(a,b): составляют множество непрерывных функций, графики которых не выходят из полосы шириной :

2. Окрестностью точки х называют любой открытый

шар с центром в этой точке.

Точка называется внутренней, если она входит во множество вместе со своей окрестностью.

Множество - открытое, если все его точки внутренние.

Пример: (a,b) - открытое множество.

7.3. ТЕРЕМА 1. Открытый шар с центром в некоторой

точке и радиусом - открытое множество.

Доказательство:

Пусть .

Построим .

Действительно: для

Ч.Т.Д.

ТЕОРЕМА 2. Объединение открытых множеств в любой совокупности и пересечение открытых множеств в конечном числе есть открытое множество, т.е.:

- открытые множества.

Доказательство:

1. открытое множество из определения. Действительно, если

, т.к. U - открытое множество. Но

. Ч.Т.Д.

2. - открытое множество. Действительно, для -открытое

множество, тогда входит в с шаром , в с шаром , ... , в с шаром . Следовательно,

. Ч.Т.Д.

Для утверждение неверно, т.к. бесконечного множества положительных чисел может быть равен нулю.

Пример: - не открытое множество.

Замкнутые множества. Замыкание.

.Множество называется замкнутым, если оно содержит в себе все свои предельные точки.

Примеры: 1. Множество точек отрезка образуют замкнутое множество. Из математического анализа известно, что все точки отрезка являются предельными, вне отрезка нет точек предельных для точек множества.

2. Множество точек интервала образуют незамкнутое множество.

Действительно, точки a и b предельные для точек данного множества, но множеству не принадлежат.

3. Множество всех действительных чисел ( точек числовой оси ) - замкнутое множество.

Замыканием множества М называется множество , где - производное множество ( множество предельных точек М ).

Очевидно, М - замкнутое множество, если . Напротив, если М - замкнутое множество, то и, следова-

тельно, (Это утверждение можно считать вторым определением замкнутого множества: множество замкнуто, если оно совпадает со своим замыканием).

Примеры: 1. Для мн-ва .

Тогда

2. Для - пустого множества имеем: .

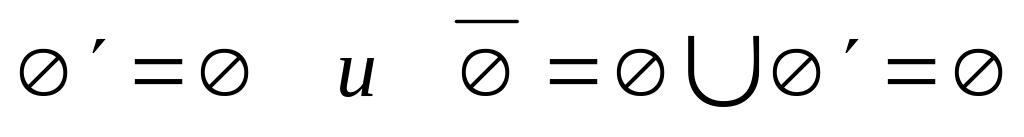Следовательно, - замкнутое множество.

ТЕОРЕМА 1. В любом метрическом пространстве замкнутый шар есть замкнутое множество.

Доказательство:

Пусть . (1)

Докажем, что не предельная точка для множества точек шара , то есть докажем, что существует , не содержащий точек

шара . Построим . Будем доказывать методом от противного: пусть и пусть

,

что противоречит условию (1). Следовательно вне шара нет предельных точек шара. Ч.Т.Д.

ТЕОРЕМА 2. Дополнение открытого множества до всего пространства всегда замкнутое. Дополнение замкнутого множества до всего пространства всегда открытое.

Доказательство:

Пусть F - замкнутое множество. Тогда U=CF - его дополнение до всего пространства. Докажем, что оно открытое.

Пусть . Допустим, что без окрестности, т. е. в любом открытом шаре с центром в точке z существуют точки множества F. Тогда z - предельная точка множества F . Т.к. F - замкнутое множество, то , что противоречит условию . Следовательно, U - открытое множество.

Пусть теперь U - открытое множество, а F=CU - его дополнение до всего пространства. Докажем, что оно замкнутое.

Действительно, вместе с некоторой окрестностью и поэтому не может быть предельной точкой множества F. Тогда все предельные точки множества F могут быть только в F . Следовательно, F - замкнутое множество

Ч.Т.Д.

Пример: Так как множество всех действительных чисел ( точек числовой оси ) - замкнутое множество, то его дополнение С = - открытое множество. Таким образом, из этого примера и примера п. 8.2 мы убедились, что является примером одновременно замкнутого множества и открытого.

Очевидно, это утверждение справедливо и для множества всех действительных чисел .

ТЕОРЕМА 3. Объединение замкнутых множеств в конечном числе и пересечение замкнутых множеств в любой совокупности есть замкнутое множество.

Доказательство:

Пусть - замкнутые множества, а - дополнительные открытые множества. Тогда из принципа двойственности имеем: - открытое множество по теореме 2 параграфа 6. Но тогда - замкнутое множество по теореме о дополнениях.

Аналогично. - открытое множество по теореме 2 параграфа 6. - замкнутое множество по теореме о дополнениях. Ч.Т.Д.