Вопросы к экзамену по дискретной математике 2015(без доказательств, вопросы к тесту)

Двузначная логика

1 Определение функции двузначной логики от n переменных и число всех функций от n переменных

Функция двузначной логики – закон , который любому упорядоченному набору нулей и единиц (x1..xn) где любой x {0,1} ставит в соответствие некоторое вполне определённое число 0 или 1. Число всех функций от n переменных

2 Определение соседних наборов.

Наборы называются соседними, если они различны только в одном разряде.

3 Определение существенной и фиктивной переменной

Переменная существенная, если существует пара соседних наборов, функции от которых имеют различные значения. Переменная фиктивная, если значения функции на всех парах соседних наборах одинаковы.

4 Дать определение и построить таблицу для импликации , функции Шеффера, стрелки Пирса и сложения по модулю 2, конъюнкции, дизъюнкции, отрицания, эквиваленции

Конъюнкция - логическая операция, истинная только тогда, когда оба исходных высказывания истинны.

Дизъюнкция - логическая операция, ложная только тогда, когда оба исходных высказывания ложны.

Отрицание - логическая операция, ложная тогда, когда исходное высказывание истинно и наоборот.

Импликация - логическая операция, ложная только тогда, когда первое исходное высказывание истинно, а второе ложно.

Эквиваленция - логическая операция, истинная тогда, когда оба исходных высказывания одинаковы.

Сложение по модулю 2 - логическая операция, истинная только тогда, когда исходные высказывания различны.

Функция Шеффера - логическая операция, ложная тогда, когда оба исходных высказывания истинны.

Стрелка Пирса - логическая операция, истинная только тогда, когда оба исходных высказывания ложны.

X	Y	Коньюн	Дизъюн	Отриц Y	Импл	Эквив	Слож	Шефф	Пирс
0	0	0	0	1	1	1	0	1	1
0	1	0	1	0	1	0	1	1	0
1	0	0	1	1	0	0	1	1	0
1	1	1	1	0	1	1	0	0	0

5 Закон коммутативности, правила поглощения

6 Закон дистрибутивности дизъюнкции относительно конъюнкции, правила расщепления

7 Закон дистрибутивности конъюнкции относительно дизъюнкции, правила де Моргана

8 Закон ассоциативности, закон двойного отрицания

9 Законы с константами

10 Определение булевой формулы

Булева формула – логическая формула, содержащая переменные и определённые связки – конъюнкцию, дизъюнкцию и отрицание. Любая формула может быть записана в форме булевой формулы.

11 Правила «поглощения отрицания», представление импликации с помощью булевой формулы

13 Представление функции Шеффера и сложения по модулю 2 с помощью булевой формулы

12 Представление стрелки Пирса и эквиваленции с помощью булевой формулы

13 Определение противоположных наборов и двойственной функции

Противоположные наборы – наборы, все значения аргументов которых взаимно противоположны.

Двойственной для функции f(x₁, x₂, …, x_n) называется функция

14 Свойства двойственных функций

А) f^*(x1,...,x_n)^*= f(x1,...,x_n)

Б) Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций.

Если h=f(g1,..gn), то h*=f*(g1*,..gn*)

15 Пары двойственных функций двузначной логики

Конъюнкция и дизъюнкция, штрих Шеффера и стрелка Пирса, эквиваленция и сложение по мод 2

16 Определение полинома Жегалкина для функции двух и трех переменных

n=2 a₀⊕a₁x⊕a₂y⊕a₁₂xy a{0,1}

n=3 a₀⊕a₁x⊕a₂y⊕a₃z⊕a₁₂xy⊕a₁₃xz⊕a₂₃yz⊕a₁₂₃xyz

17 Представление основных функций полиномами Жегалкина

18 Определение полной конъюнкции n переменных. Определение СДНФ

СДНФ – функция ДНФ, которая удовлетворяет требованиям полной конъюнкции:

А) в каждой элементарной конъюнкции участвуют все n переменных

Б) каждая переменная встречается 1 раз( с отрицанием или без)

В) все элементы конъюнкции различны, нет одинаковых.

19 Определение полной дизъюнкции n переменных. Определение СКНФ

СКНФ – функция КНФ, которая удовлетворяет требованиям полной дизъюнкции:

А) в каждой элементарной дизъюнкции участвуют все n переменных

Б) каждая переменная встречается 1 раз( с отрицанием или без)

В) все элементы дизъюнкции различны, нет одинаковых.

20 Определение замкнутого класса. Дать определение линейной функции.

Р={f1,..,fn} является замкнутым классом, если его замыкание относительно операции суперпозиции совпадает с ним самим: [P]=P

Булева функция f(x1,...,x_n) называется линейной, если существуют такие a₀,a₁,a₂,..,a_n (a_i{0,1}), что для любых x₀,x₁,x₂,..,x_n имеет место равенство: f(x1,...,x_n)=a₀⊕a₁x₁⊕a₂x₂⊕..⊕a_nx_n

21 Дать определение сравнимых наборов, монотонной и немонотонной функции

Альфа и бэта

Наборы являются сравнимыми, если A(a₁..a_n), B(b₁..b_n) A_i<=B_i i{1..n} Функция монотонна если для всех A<B и f(A)<=f(B) Функция не монотонна если хотя бы для одного A<B и f(A)>f(B) 22 Дать определение самодвойственной функции и функции, сохраняющей 0 и 1.

функция f(x₁, x₂, …, x_n) является самодвойственной, если

Функция сохраняющая 0 - логическая функция, значение которой равно 0, если все аргументы равны 0: f(0,0,...,0) = 0.

Функция сохраняющая 1 - логическая функция, значение которой равно 1, если все аргументы равны 1: f(1,1,...,1) = 1.

23 Определение полной системы, теорема Поста

Система является полной, если множество функций, входящих в эту систему совпадает с замыканием этого множества [P]=P₂.

Теорема Поста – Набор булевых функций P является полным тогда и только тогда, когда он не содержится полностью ни в одном из классов (T₀,T₁,L,S,M)

К-значная логика

1 Определение функции k-значной логики. Сколько всего функций к-значной логики от n переменных

В   k- значной логике значения аргументов и значения функции могут принимать любые значения из следующего множества  {0, 1, …, к-1}. Число всех функций k-значной логики от n переменных равно

2 Определение функций j_i(x), x⊃y, x÷y, J_i(x), x-y , x(отриц), -x,  ~x, V_k(x,y)

3 Закон коммутативности и ассоциативности для функций k-значной логики. Какие функции ему удовлетворяют?

Коммутативность: x0y=y0x 0{+,*,max,min}

Ассоциативность: x0(y0z)=(x0y)0z 0{+,*,max,min}

4 Закон дистрибутивности max относительно min и min относительно max

1). Дистрибутивность функции  max  относительно функции   min : 

     max [ min(x, y), z ] = min [ max(x, y), max(y, z) ].

2). Дистрибутивность функции   min относительно функции   max :

      min [ max(x, y), z ] = max [ min(x, z), min(y, z) ].

5 Закон двойного отрицания. Удовлетворяет ли этому закону отрицание Поста?

Закон двойного отрицания в двузначной логике возвращает исходное значение выражению под двойным отрицанием. Закон Поста не удовлетворяет этому закону, так как он гласит x(отриц)=х+1 (mod k), х(дв.отриц)=(х+1)(отриц)( mod k)=х+2 (mod k). Чтобы вернуться к х, нужно чтобы количество операций отрицания Поста было проведено k раз.

6 Дать определение функций: отрицание Лукашевича и отрицания Поста. Какая из функций удовлетворяет закону двойного отрицания?

Отрицание Лукашевича ~x=(к-1)-х , удовлетворяет закону двойного отрицания, так как при двойном его применении мы вернём первоначальное значение переменной ~( ~x)= ~(k-1-x)=k-1-(k-1-x)=k-k-1+1+x=x . Отрицание Поста не удовлетворяет закону двойного отрицания, так как х(дв.отриц)=(х+1)(отриц)( mod k)=х+2 (mod k).

7 Аналоги правил де Моргана в к-значной логике

min( ~x,~y)=~max( x, y );        

max( ~x,~y)=~min( x, y).

8 Определение I формы для функции k-значной логики. Аналогом какой формы для функции 2значной логики она является?

I форма для функции k-значной логики – способ представления функции f(x₁..x_n) , являющийся аналогом СДНФ для функций двузначной логики. f(x₁..x_n)=max(min(f(x₁..x_n),J_1(x₁),J_2(x₂)…J_n(x_n)),…) Где максимум берётся по всем наборам f(₁.. _n) значений переменных х₁..x_n

9 Определение II формы для функции k-значной логики. Аналогом какой формы для функции 2значной логики она является?

II форма для функции k-значной логики – способ представления функции f(x₁..x_n) , являющийся аналогом полинома Жигалкина для функций двузначной логики. f(₁.._n)= Где суммирование ведётся по всем наборам f(₁.. _n) значений переменных х₁..x_n

10 Определение III формы для функции k-значной логики. Аналогом какой формы для функции 2значной логики она является?

III форма для функции k-значной логики – способ представления функции f(x₁..x_n) , являющийся аналогом СКНФ для функций двузначной логики. f(x₁..x_n)=min(max(f(₁.._n), ~J_1(x₁), ~J_2(x₂)… ~J_n(x_n)),…) Где минимум берётся по всем наборам f(₁.. _n) значений переменных х₁..x_n.

11 Представление функций j_i(x) полиномом по модулю k

J₀(x)=1-x^k-1 j_=1-(x-)^k-1 и подставляем их во II форму с учётом mod k

12 Определение полинома по модулю k для функции 1 переменной.

F(x)=f(x₁)*j0(x)+…+f(x_k)*j_k-1(x)

13 Теорема о представлении функции полиномом по модулю k. Можно ли разложить в полином функцию j₀(x) при k=25?

Теория графов

1.Абстрактный граф

Абстрактный граф – это граф заданный непустым множеством вершин V={V1, V2..Vn}, множеством ребер x(Vi, Vj).

2. Абстрактный ориентированный граф

Абстрактный ориентированный граф – задается непустым множеством вершин V={V1, V2..Vn}, множеством ребер x(Vi, Vj) (с упорядоченным направлением из Vi в Vj).

3. Кратные рёбра и петли

Кратные ребра – ребра с общими вершинами. Петля – ребро, концы которого совпадают.

4. Смежные вершины, изолированные вершины

Смежные вершины – 2 вершины инцидентные одному ребру.

Изолированная вершина -  вершина, степень которой равна 0 (то есть нет ребер, инцидентных ей).

5. Псевдограф (ориентированный псевдограф)

Псевдограф - граф, который может содержать петли и/или кратные рёбра.

6. Мультиграф (ориентированный мультиграф)

Мультиграф – граф, который может содержать кратные ребра, но не содержащий петель.

7. Матрица смежности графа (орграфа)

Матрица смежности – это матрица n x n (где n – число вершин), в которой каждый элемент а(i,j) равен числу ребер, соединяющих V(i) и V(j).

7.1 определение полного и двудольного графа

Полный граф - граф, у которого каждая пара вершин соединена ребром. Полный n -вершинный граф обозначается G_n.

Двудольный граф - граф, у которого существует такое разбиение множества вершин на две части (доли), что концы каждого ребра принадлежат разным долям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным.

8. Матрица инцидентности неориентированного графа

Матрица инцидентности графа – это матрица n x m, в которой b(i,j)=0 если v(i) не инц x(j), 1 если v(i) инц ребру x(j).

9. Матрица инцидентности орграфа

Матрица инцидентности орграфа – это матрица n x m, в которой b(i,j)=0 если v(i) не инц x(j), 1 если v(i) – конец x(j), -1 если v(i) начало x(j).

10. Степень вершины, полустепени захода и полустепени исхода в орграфе.

Степень вершин графа – deg V(i)= число инц. ребер. Вклад петли = 2

Полустепень: Исхода deg- V(i)- число выходящих ребер. Захода deg+ V(i) – число заходящих ребер. Для петли вклад в полустепени и исхода и захода =1

11. найти сумму степеней всех вершин в графе

сумма deg V(i)=2m (где m – число ребер)

12. найти сумму полустепеней исхода (захода) в орграфе

сумма deg+ V(i)+ deg- V(i)=2m

13. как найти степень вершины по матрице смежности мультиграфа?

Deg V(i)=сумма элементов i строки или i столбца

14. как найти степень вершины по матрице инцидентности графа?

Сумма элементов    i - ой   строки матрицы инцидентности графа равна Deg V(i)

15. как найти полустепень исхода (захода) по матрице смежности ориентированного мультиграфа?

Сумма элементов  i - ой строки матрицы смежности ориентированного мультиграфа равна Deg-V(i) , а сумма элементов i – го   столбца – Deg+ V(i)

16. Изомрфный граф

Графы и  изоморфны, если существует такое взаимно однозначное соответствие между множествами их вершин v и v’, что вершины соединены ребрами в одном из графов в том и только том случае, когда соответствующие им вершины соединены в другом графе.

17. Подразбиения ребра (дуги)

Операция подразбиения (измельчения) дуги (u, v) в орграфе D = (V, E) состоит в удалении из Е дуги (u, v), добавлении к V новой вершины w и добавлении к Е | {(u, v)} двух дуг (u, w), (w, v). Аналогично определяется операция подразбиения ребра в графах.

18. гомеоморфные графы

Орграфы D1, D2 называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.

19. Правильно реализованный граф

граф называется правильно реализованным (или правильным), если его дуги не имеют общих точек, отличных от вершин графа.

20. Плоский (планарный) граф

Планарный граф — граф, который может быть изображён на плоскости без пересечения ребер.

21. нарисовать графы G₅ и G_3,3 . Являются ли они планарными?

22. Теорема Понтрягина-Куратовского

Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных К₅ или К_3,3 .

23. маршрут в графе (пути в орграфе)

Маршрут в графе (путь в орграфе) из вершины i в вершину j – последовательность вершин и ребер (дуг), инцидентных двум соседним вершинам.

24. длина маршрута, пути

Длиной маршрута(пути) называется количество ребер(дуг) в нем. 25. цепь, простой цепь

Цепь (орцепь) – маршрут (путь), в котором ребра (дуги) проходятся один раз. Простая цепь (простая орцепь) – цепь (орцепь) без повторяющихся вершин.

26. цикл (контур), простой цикл (контур)

Цикл – замкнутая цепь. Контур – замкнутая орцепь.

27. укажите, как определить число всех путей длины k из вершины v1 в v2 в графе(орграфе)

Возвести матрицу смежности этого графа(орграфа) в степень k, число a^k (1,2)– число путей из v1 в v2

28. как определить наличие циклов в ориентированном псевдографе графе с n вершинами.

В ориентированном псевдографе есть цикл, если в нём есть петли или же есть рёбра с различными направлениями из одной вершины

29. как определить наличие пути из вершины v1 в v2 в графе с n вершинами.

Путь в графе между вершинами v1 и v2 существует, если они соединены ребром или же соединены такой последовательностью рёбер и вершин, что каждые два соседних ребра последовательности имеют общую вершину.

30. расстояние в графе между v1 и v2

В теории графов расстоянием между двумя вершинами графа называется число рёбер в кратчайшем пути (также называемым геодезической графа). D(Vi, Vj).

31. Диаметр графа

Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.

32. эксцентриситет вершины v(i)

Эксцентриситетом e вершины v(i) называется наибольшее кратчайшее (геодезическое) расстояние между v(i) и любой другой вершиной.

33. Радиус графа

Радиусом r графа называется минимальный эксцентриситет любой вершины, или, формально, r=min e(v).

34. Центр графа

Центральной вершиной графа радиусом r называется вершина, эксцентриситет которой равен r

35. эйлерова цепи и цикл, эйлеров и квазиэйлеров граф

Эйлеров путь (эйлерова цепь) в графе — это путь (цепь), проходящий по всем дугам (рёбрам) графа и притом только по одному разу. Эйлеров цикл — это цикл графа, проходящий через каждое ребро (дугу) графа ровно по одному разу. Эйлеров граф — граф, содержащий эйлеров цикл. Квазиэйлеров граф — граф, содержащий эйлеров путь (цепь).

36. гамильтонова цепь и цикл, гамильтонов и квазигамильтонов граф

Гамильтоновым путём (англ. Hamiltonian path) называется простой путь, приходящий через каждую вершину графа ровно один раз. Гамильтоновым циклом (англ. Hamiltonian cycle) называют замкнутый гамильтонов путь.

Граф называется гамильтоновым (англ. Hamiltonian graph), если он содержит гамильтонов цикл. Граф называется квазигамильтоновым (англ. Semihamiltonian graph), если он содержит гамильтонов путь. 37. Теорема Эйлера (необходимое и достаточное условие эйлерова графа)

Связный неориентированный псевдограф тогда и только тогда является эйлеровым (т. е. обладает эйлеровым циклом), когда степень каждой его вершины есть четное число.

38. Необходимое и достаточное условие квазиэйлеровости графа

Связный неориентированный псевдограф тогда и только тогда является квазиэйлеровым (т. е. обладает эйлеровым путём), когда существует цепь, проходящая через каждое его ребро.

37 Комбинаторные схемы суммы и произведения. Перестановки, размещения, сочетания. Примеры.

Правило суммы: Если элемент A можно выбрать m способами, а элемент B можно выбрать k способами, то выбор элемента A или B можно осуществить m + k способами.

Правило произведения: Если элемент A можно выбрать m способами, а после каждого выбора элемента A элемент B можно выбрать k способами, тогда, упорядоченную пару элементов (A, B) можно выбрать m*k способами.

Число перестановок - n!

A^k_n = (n - 1)(n - 2) … (n - k + 1)

Размещениями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение по k элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения. C_n^k=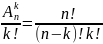 = Сочетание - Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается

17.Алгоритм фронта волны

Пусть D  (V , X ) ориентированный граф с n2 вершинами и v,w (vw) – заданные вершины из V.

1) Помечаем вершину v индексом 0, затем помечаем вершины  образу вершины v индексом 1. Обозначаем их FW1 (v). Полагаем k=1.

2) Если FW k ( v )   или k=n-1, и одновременно w FW ( v )  k то вершина w не достижима из v . Работа алгоритма заканчивается. В противном случае продолжаем:

3) Если  ( ) k w FW , то переходим к шагу 4. В противном случае мы нашли минимальный путь из v в w и его длина равна k. Последовательность вершин есть этот минимальный путь. Работа завершается. 4) Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом k. Множество вершин с индексом k+1 обозначаем ( ) 1  k  FW . Присваиваем k:=k+1 и переходим к 2).

16. Алгоритм Терри поиска пути

Пусть дан неориентированный граф G(V, Q) - связный.

Найдём путь из вершины vi в вершину vj (поиск выхода из лабиринта)

1. Проходя какое-либо ребро, помечаем направление, в котором мы его проходим.

2. Если в вершину vi первый раз мы пришли по ребру qk, то это ребро помечаем.

3. Идти можно только по ребру, которое не было пройдено, или было пройдено в противоположном неправлении.

4. Из вершины vi по ребру qk (помеченному в пункте 2) можно идти в обратном направлении только когда других возможностей нет, т.е. все рёбра, инцидентные vi пройдены по два раза (туда и обратно).

15. Алгоритм Флери поиска эйлеровой цепи, цикла пути

Алгоритм Флёри достаточно прост в применении. Суть его заключается в следующем: выходим из произвольной вершины графа, соблюдая два правила:

все рёбра, по которым мы проходим, стираются, так же как и появившиеся в результате изолированные вершины;

на каждом шаге идём по мосту только тогда, когда нет других возможностей.

Мост — это такое ребро графа, при стирании которого граф становится несвязным: