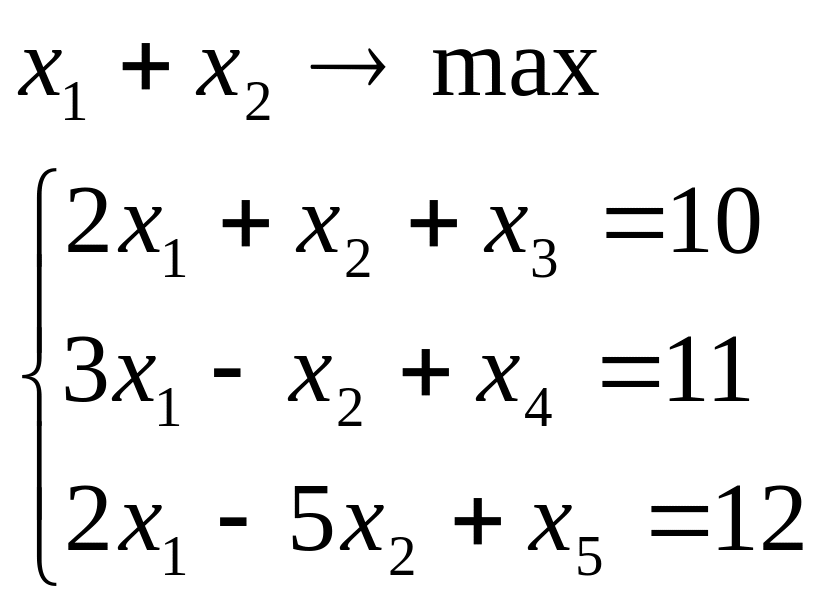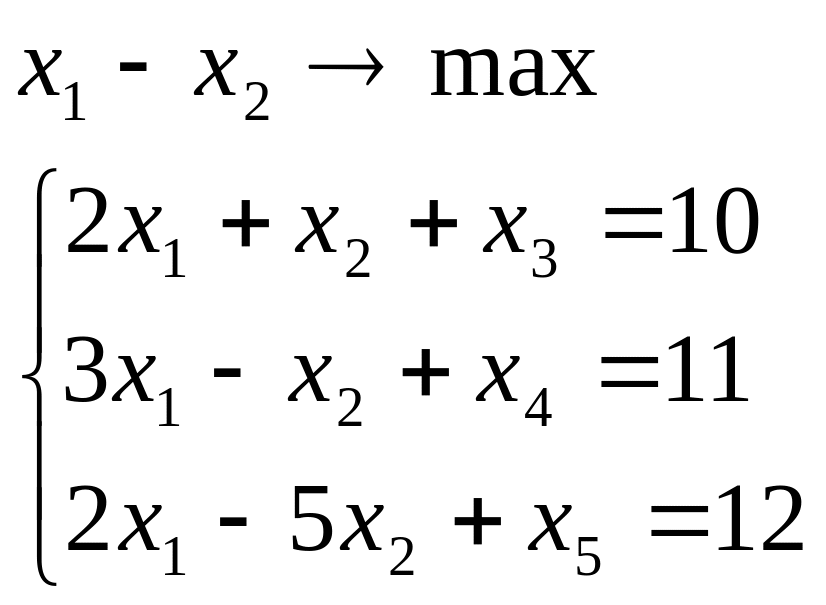- •Тема 1. Концептуальні аспекти математичного моделювання економіки.
- •Тема 2. Оптимізаційні економіко-математичні моделі
- •Тема 3. Задача лінійного програмування та методи її розв'язування.
- •Тема 4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач.
- •Тема 5. Транспортна задача. Методи розв’язування
- •Тема 6. Цілочислові задачі лінійного програмування
- •Тема 7. Класичні методи рішення нелінійних оптимізаційних моделей
- •Тема 8.Моделі опуклого програмування
- •Тема 9.Основні типи задач та моделі динамічного та мережного програмування.
- •Тема 10. Елементи теорії ігор
Тема 3. Задача лінійного програмування та методи її розв'язування.
Що відповідає в
Декартові системі координат рівнянню
виду:
|
пряма паралельна осі ох1 |
*пряма паралельна осі ох2 |
бісектриса першого квадранту |
немає вірної відповіді |
Для яких економічних систем можна використовувати в якості моделі задачу лінійного програмування про суміші ? |
*При складання раціону харчування корів |
При складанні виробничої програми підприємства |
При визначенні послідовності виконання робіт |
При визначенні коштів міжгалузевого балансу |
Для яких економічних систем можна використовувати в якості моделі задачу лінійного програмування про раціональна використання потужностей ? |
При складання раціону харчування корів |
При складанні виробничої програми підприємства |
*При визначенні послідовності виконання робіт |
При визначенні коштів міжгалузевого балансу |
Для яких економічних систем можна використовувати в якості моделі задачу лінійного програмування про розподіл ресурсів на випуск продукції ? |
при складання раціону харчування корів |
*при складанні виробничої програми підприємства |
при визначенні послідовності виконання робіт |
при визначенні коштів міжгалузевого балансу |
Якій рядок в М-методі обирається для виділення розв’язувального рядка? |
*рядок, що містить штучну змінну |
рядок, що має найбільшу оцінку |
рядок, що має найменшу оцінку |
будь-якій рядок |
Як в М-методі для виділення розв’язувального стовпця обирається елемент? |
найбільший по модулю елемент розв’язувального рядка |
*найбільший по модулю елемент розв’язувального рядка такого ж знаку, що і вільний член цього рядка |
найбільший по модулю елемент рядка цілі |
найменший елемент стовпця оцінок |
Що обирається для виділення в М-методі спочатку? |
*розв’язувальний рядок |
розв’язувальний стовпець |
розв’язувальний елемент |
функція цілі |
Відмітьте матричну форму запису ЗЛП... |
*сх(max) ax=b |
|
|
|
Які змінні для
даної ЗЛП ввійдуть в базис
|
|
|
|
* |
Які змінні для
даної ЗЛП ввійдуть в базис
|
|
|
|
* |
Для змінних , що не увійшли в план транспортної задачі чому дорівнює оцінка в матриці оптимальності? |
дорівнює 0 |
більша 0 |
менша 0 |
*не дорівнює 0 |
Для змінних , що увійшли в план транспортної задачі чому дорівнює оцінка в матриці оптимальності? |
*дорівнює 0 |
більша 0 |
неменша 0 |
не більша 0 |
Які методи відносять до методів розв’язку ЗЛП? |
градієнтний метод |
метод потенціалів |
симплекс метод |
*всі відповіді вірні |
Яким вимогам задовольняє допустиме рішенням ЗЛП ? |
* цє вектор, що задовольняє всім обмеженням задачі |
цє вектор, що задовольняє функції цілі задачі |
цє вектор, що задовольняє одночасно обмеженням та функції цілі |
цє вектор, що задовольняє деяким обмеженням та функції цілі |
Якою буває задача лінійного програмування … |
*стандартною |
довільною |
*двоїстою |
стохастичною |
Як з задач є задачею лінійного програмування ? |
стандартною |
транспортною |
двоїстою |
*всі відповіді вірні |
Знайдіть з переліченого задачу лінійного програмування ? |
*немає вірної відповіді |
довільною |
строгою |
квадратичною |
Яка задача називається змішаною задачею ЗЛП ? |
всі обмеження - нерівності |
всі обмеження рівності |
*обмеження можуть бути рівностями та нерівностями |
немає вірної відповіді |
Змінна що відповідає розв’язувальному рідку в симплекс методі входить чи виходить з базису? |
*виходить з базису |
входить в базис |
використовується для перевірки задачі на оптимальність |
використовується для заповнення стовпця оцінок |
Змінна що відповідає розв’язувальному стовпцю в симплекс методі входить чи виходить з базису? |
виходить з базису |
*входить в базис |
використовується для перевірки задачі на оптимальність |
використовується для заповнення стовпця оцінок |
Канонічною задачею називається задача ЗЛП у якої особливий вид обмежень?. Який? |
всі обмеження - нерівності |
*всі обмеження рівності |
обмеження можуть бути рівностями та нерівностями |
немає вірної відповіді |
Що відповідає кожному допустимому базисному рішенню ЗЛП?. |
*кутова точка многокутника рішень |
внутрішня точка многокутника рішень |
довільна точка многокутника рішень |
довільна точка функції цілі |
Коли деяке обмеження задачі на оптимальному рівні не перетворюється на точну рівність, то як веде себе відповідна невідома оптимального плану двоїстої задачі? |
*відповідна невідома оптимального плану двоїстої задачі дорівнює нулю |
відповідна невідома оптимального плану двоїстої задачі більше нуля |
відповідна невідома оптимального плану двоїстої задачі менше нуля |
відповідна невідома оптимального плану двоїстої задачі менше або дорівнює нулю |
Коли ставиться оцінка розв’язувального стовпця? |
*коли відповідний вільний член і елемент розв’язувального стовпці мають однакові знаки |
коли відповідний вільний член і елемент розв’язувального стовпці мають різні знаки |
коли відповідний елемент розв’язувального стовпця дорівнює 0 |
завжди |
Критерій оптимальності при розв’язуванні задачі на максимум симплекс методом? |
якщо в останньому рідку всі числа невід’ємні |
якщо в останньому рідку всі числа не додатні |
*якщо в останньому рідку всі числа невід’ємні, крім стовпця вільних членів |
якщо в останньому рідку всі числа не додатні, крім стовпця вільних членів |
Критерій оптимальності при розв’язуванні задачі на мінімум симплекс методом? |
якщо в останньому рідку всі числа невід’ємні |
якщо в останньому рідку всі числа не додатні |
якщо в останньому рідку всі числа невід’ємні, крім стовпця вільних членів |
*якщо в останньому рідку всі числа не додатні, крім стовпця вільних членів |
М- метод - це метод пошуку рішення яких задач? |
*лінійного програмування |
нелінійного програмування |
динамічного програмування |
квадратичного програмування |
М метод штучного базису рішення задачі лінійного програмування необхідний. для пошуку чого? |
*для пошуку початкового допустимого базисного рішення |
для пошуку оптимального рішення |
для визначення базису, що виходить з плану |
для перерахунку коефіцієнтів нової симплекс таблиці |
Пошук чого відбувається на першому етапі розв’язку задач лінійного програмування? |
*допустимого базисного рішення задачі |
будь-якого базисного рішення задачі |
заповнення симплекс таблиці |
перевірка задачі на задоволення умовам оптимальності |
Що відповідає
нерівності виду:
|
*пряма |
багатокутник |
площина |
півплощина |
Що відповідає нерівності виду:
|
пряма |
багатокутник |
площина |
*півплощина |
Що відповідає
нерівності виду:
|
пряма |
багатокутник |
площина |
*півплощина |
Що називається оптимальним планом (рішенням) задачі лінійного програмування ? |
*рішення системи обмежень, що задовольняє цілі |
єдине рішення системи обмежень |
будь-яке рішення системи обмежень |
будь-яке значення функції цілі |
Який вектор задовольняє оптимальному рішенню ЗЛП ? |
всім обмеженням задачі |
функції цілі задачі |
*одночасно обмеженням та функції цілі |
деяким обмеженням та функції цілі |
Для чого використовується правило прямокутника? |
*пошуку коефіцієнтів нової симплекс таблиці |
пошуку нового базисного рішення |
перевірки задачі на оптимальність |
заповнення стовпця оцінок |
Як взаємно
розташовані прямі
|
*паралельні |
перетинаються |
співпадають |
перпендикулярні |
Як взаємно
розташовані прямі
та
|
паралельні |
перетинаються |
*співпадають |
перпендикулярні |
Як взаємно
розташовані прямі
та
|
паралельні |
*перетинаються |
співпадають |
перпендикулярні |
Як взаємно
розташовані прямі
та
|
паралельні |
перетинаються |
співпадають |
*перпендикулярні |
Як взаємно
розташовані прямі
|
*паралельні |
перетинаються |
співпадають |
перпендикулярні |
Як взаємно
розташовані прямі
та
|
паралельні |
перетинаються |
*співпадають |
перпендикулярні |
Як взаємно
розташовані прямі
та
|
паралельні |
*перетинаються |
співпадають |
перпендикулярні |
Як взаємно
розташовані прямі
|
паралельні |
перетинаються |
співпадають |
*перпендикулярні |
Що відповідає
рівнянню виду:
|
*пряма |
багатокутник |
площина |
півплощина |
Що відповідає рівнянню виду: в Декартові системі координат ? |
пряма паралельна осі ох1 |
*пряма паралельна осі ох2 |
бісектриса першого квадранту |
немає вірної відповіді |
Що відповідає
рівнянню виду:
|
пряма паралельна осі ох1 |
пряма паралельна осі ох2 |
бісектриса першого квадранту |
*немає вірної відповіді |
Що відповідає
нерівність виду:
|
пряма |
багатокутник |
площина |
*півплощина |
Що відповідає
рівнянню виду:
|
*пряма паралельна осі ох1 |
*пряма паралельна осі ох2 |
бісектриса першого квадранту |
немає вірної відповіді |
Що відповідає
рівнянню виду:
|
*пряма паралельна осі ох1 |
пряма паралельна осі ох2 |
бісектриса першого квадранту |
немає вірної відповіді |
Що відповідає
рівнянню виду:
|
пряма паралельна осі ох1 |
пряма паралельна осі ох2 |
бісектриса першого квадранту |
*немає вірної відповіді |
Серед заданих постановок ЗЛП відмітьте загальну (змішану) постановку задачі |
|
* |
|
|
Серед заданих постановок ЗЛП відмітьте канонічну постановку задачі |
* |
|
|
|
Серед заданих постановок ЗЛП відмітьте стандартну постановку задачі |
|
|
* |
|
Що відповідає
системі нерівностей виду: |
*пряма |
багатокутник |
пуста множина |
півплощина |
Що відповідає системі нерівностей виду:
|
пряма |
багатокутник |
*пуста множина |
півплощина |
Що відповідає
системі нерівностей виду: |
пряма |
багатокутник |
*площина |
півплощина |
Яка задача називається стандартною задачею ЗЛП |
*задача ЗЛП де всі обмеження - нерівності |
задача ЗЛП де всі обмеження рівності |
задача ЗЛП де обмеження можуть бути рівностями та нерівностями |
немає вірної відповіді |
Як називається стовпець що відповідає змінній з мінімальним від’ємним числом при рішенні задачі на максимум? |
*розв’язувальим |
оптимальним |
базисним |
вірної відповіді немає |
Як називається така форма запису умови лінійної задачі СХ(max) AX=B? |
*матричною |
векторною |
алгебраїчною |
немає вірної відповіді |
Яка функція цілі ЗЛП ? |
|
* |
|
|
Чи існує базис в даній ЗЛП
|
*так |
ні |
іноді |
немає вірної відповіді |
Чи існує базис в даній ЗЛП
|
так |
*ні |
іноді |
немає вірної відповіді |
Чи існує базис в даній ЗЛП
|
так |
*ні |
іноді |
немає вірної відповіді |
Чи існує базис в даній ЗЛП
|
*так |
ні |
іноді |
немає вірної відповіді |
Чи належить точка (-3;3) множині 3х1 –4х2 <=-12 |
*так |
ні |
частково |
немає вірної відповіді |
Яка з умов є характеристикою базисної змінної? |
вона основна |
*вона існує тільки в одному рівнянні системи обмежень |
*вона штучна |
вона є залежною |
Яка з умов не є обов’язковою умовою базисної змінної? |
наявність цієї змінної тільки в одному рівнянні системи обмежень |
*вона залежна |
змінна не входить в функцію цілі |
коефіцієнт змінної +1, за умови, що вільний член додатній |
Яка задача не відноситься до задач лінійного програмування? |
задач про склад раціону годівлі |
задача про використання ресурсів |
задача про використання потужностей |
*задача управління капіталовкладеннями |
Яка задачі можна розв’язати методами лінійного програмування? |
задачі про склад раціону годівлі |
задачі про використання ресурсів |
задачі про вибір маршруту |
*усі відповіді вірні |
Яким методом
можна розв’язати дану ЗЛП |
*симплекс методом |
методом Беллмана |
методом потенціалів |
методом штучного базису |
Яким методом
можна розв’язати дану ЗЛП |
симплекс методом |
методом Беллмана |
методом потенціалів |
*методом штучного базису |
Які з методів не є методом побудови початкового плану ТЗ |
метод північно-західного кута |
метод мінімального елемента |
метод усереднених коефіцієнтів |
*симплекс метод |
Якій метод не відносять до методів пошуку початкового базисного рішення транспортної задачі? |
метод північно західного кута |
метод усереднених коефіцієнтів |
метод мінімального елемента |
*метод пропорцій |
Якщо в симплекс таблиці існує розв’язувальний стовпець, а в стопці оцінок відсутні числа, то що можна сказати про рішення ЗЛП? |
задача розв’язана |
задача зациклена |
*задача не має розв’язку |
вірної відповіді немає |
Якщо за задача задана в канонічному вигляді і існує базис, то що треба зробити на першому етапі її розв’язку ? |
побудувати потенціали |
звести її до стандартного виду |
*заповнити першу симплекс таблицю |
вірної відповіді немає |
Якщо за задача задана в канонічному вигляді на першому етапі її розв’язку симплекс методом що треба зробити? |
*перевірити її на наявність базису |
звести її до стандартного виду |
заповнити першу симплекс таблицю |
вірної відповіді немає |
Якщо за задача задана в стандартному вигляді на першому етапі її розв’язку симплекс методом що треба зробити |
*звести задачу до канонічного вигляду |
перевірити задачу на наявність базису |
заповнити першу симплекс таблицю |
вірної відповіді немає |
Якщо ЗЛП задана в стандартному вигляді, то для перетворенні її в канонічний вид що потрібно зробити? |
ввести штучні змінні |
*ввести додаткові змінні |
помножити кожну нерівність на -1 |
немає вірної відповіді |
Якщо лінія рівня функції цілі в напрямку спадання завжди перетинає многокутник обмежень. Чи існує мінімуму функції цілі? |
так |
*ні |
в залежності від вигляду функції цілі |
в залежності від вигляду області обмежень |
Якщо лінія функції цілі співпадає в напрямку зростання з граничною лінією многокутника рішень. Чому дорівнює максимуму функції цілі? |
*всім точка цього відрізка. |
координатам вершин многокутника рішень, що відповідають цьому відрізку. |
максимум не існує |
координатам середини граничної лінії |
Якщо система обмежень задачі лінійного програмування складається з одних нерівностей, то якого типу ця задача? |
*стандартною |
канонічною |
двоїстою |
прямою |
Якщо система обмежень задачі лінійного програмування складається з одних рівнянь, то якого типу ця задача? |
стандартною |
*канонічною |
двоїстою |
прямою |
Геометричний метод в оптимізації задач лінійного програмування застосовується коли кількість змінних дорівнює... |
одній |
*двом |
трьом |
більше двох |
Після побудови області обмежень, який наступний етап в алгоритмі геометричного методу рішення задач лінійного програмування? |
побудова прямої цілі при початкових умовах |
побудова прямої цілі при умовах її зростання |
побудова прямих цілі, що проходять через многокутник обмежень |
*побудова прямих цілі, що проходять через вершини многокутника обмежень |
Як розташовані лінії рівня функції цілі в геометричній інтерпретації рішення задачі лінійного програмування ? |
*паралельні |
перпендикулярні |
довільні |
співпадають |
Яким буває симплекс метод? |
прямим |
двоїстим |
модифікованим |
*усі відповіді вірні |