15

Этапы моделирования

1. Основные понятия

Суть моделирования состоит в замене исходного объекта упрощенной копией – математической моделью (ММ) и дальнейшем изучении модели с помощью вычислительно-логических алгоритмов, реализуемых на компьютерах. При исследовании любой системы методами математического моделирования возможно наличие нескольких альтернативных вариантов модели. Каждая из них в чем-то лучше других, а чем-то хуже. Поэтому процесс построения наилучшего, как правило, компромиссного варианта модели, достаточно сложен. Системный подход предполагает наличие следующих этапов создания модели.

1. Определение цели моделирования. Любая ММ является не просто образом -заменителем оригинала, а отображением целевым. Т.е. модель всегда создаётся с определённой целью и в модели отображаются не полностью весь объект-оригинал, а только то, что в нем нас интересует с точки зрения поставленной цели. Иными словами вид создаваемой модели существенно зависит от цели моделирования. Поэтому прежде чем начинать создавать модель, надо приложить достаточное количество умственных усилий и потратить достаточно времени, чтобы определить, для чего нам нужна модель,

2. Синтез модели – создание возможных ее вариантов. Различают

а) структурный синтез – разработка структуры модели: ее общего вида (например, в виде систем уравнений, алгебраических или дифференциальных), определение числа параметров и т.п.;

б) параметрический синтез – поиск числовых значений параметров модели. Производится либо на основании справочных данных, либо исходя из условия максимального совпадения результатов, найденных по модели с экспериментальными.

3. Анализ модели – определение качества синтезированного варианта модели по критериям:

а) универсальности – полноты отображаемых свойств объекта;

б) точности – степени совпадения реальных данных с предсказанными моделью;

в) адекватности – способности правильно отображать свойства объекта в рамках цели моделирования (решаемой задачи) ;

г) экономичности – затрат на разработку и реализацию модели.

4. Выбор и принятие решения – общая оценка полезности вариантов модели и выбор лучшего.

В процессе перехода от словесного описания объекта к получению результатов исследования модель объекта претерпевает определённые изменения формы своего представления. Принято процесс возникновения и развития произвольной системы именовать термином “жизненный цикл”. В данном случае речь идёт о жизненном цикле модели, а формы представления модели называются также этапами её жизненного цикла.

Итак, существуют следующие этапы жизненного цикла математической модели.

1. Постановка задачи на неформальном уровне – словесное описание объекта и цели моделирования

2. Модель описания – описание свойств объекта и цели моделирования с помощью математических символов и соотношений.

3. Модель решения – системы математических соотношений, позволяющих получить решение поставленной задачи. Существуют несколько альтернативных типов этой модели.

а) аналитическая модель – явное выражение, позволяющее вычислить искомую величину;

б) численная модель – набор выражений, позволяющих получить решение в виде набора чисел;

в) имитационная модель – переложение на язык компьютера формальных правил функционирования моделируемого объекта; она позволяет при заданном входе получить значение выхода и по сути дела реализует метод проб.

Пример. Пусть имеем уравнение аx² + bx + c = 0, которое описывает некоторый объект и, следовательно, является моделью описания. Описание способа нахождения значения х представляет собой модель решения. Для квадратного уравнения существует известная формула:

Это явное выражение для искомой величины х, следовательно, это аналитическая модель решения.

В том случае, когда аналитическая модель слишком сложная (формулы решения уравнений 3-й и 4-й степени) либо вообще не существует (для уравнений 5-й степени и выше), то используется численная модель.

Например: дано уравнение f(x) = 0, где f – произвольная непрерывная функция. Для решения можно использовать численный метод Ньютона (ка­сательных). Для этого выбирают начальное приближение x₀, а затем строят последовательность уточняющих решений по формуле:

x_{k + 1} = x_k – ( k = 0, 1…); .

Для приближённого решения уравнения f(x) = 0 можно также задать достаточно много различных значений x и выбрать то из них, для которого | f(x) | = min, т.е. f(x) ближе всего к 0. Можно считать, что это простейший вид имитационной модели.

Часто в качестве значений входных параметров берутся случайные значения, полученные с помощью датчиков случайных чисел. В этом случае говорят, что используется случайная имитация.

Дадим краткую характеристику каждой модели, которая поможет вы­бирать ту или иную модель в каждом конкретном случае.

Аналитическая модель является наиболее точной, кроме того, она по­зволяет получить решение в общем виде. Поэтому если это возможно, всегда надо стараться получить именно аналитическую модель решения.

Численная модель более универсальна, практически не уступает по точности аналитической модели, но не позволяет получить решение в общем виде.

Имитационная модель наименее точна, но является самой простой. Её используют для получения окончательного решения только при моделирова­нии очень сложных объектов, для которых невозможно составить прочие модели решений. В более простых случаях имитационную модель применяют для поиска начального приближения к решению для дальнейшего его уточнения с помощью численной модели, либо для предварительного анализа объекта, позволяющего получить неко­торое начальное представление о предмете моделирования.

4. Алгоритмическая модель – запись решения в виде алгоритма.

Разница между 3 и 4 формой состоит в том, что модель решения не обязана обладать всеми свойствами алгоритма: конечность, определённость, результативность, массовость, эффективность. Чаще всего модель решения не обладает свойством конечности.

5. Программная модель – запись алгоритма на языке программирова­ния.

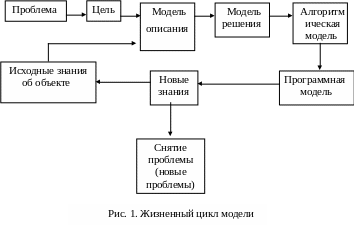
Жизненный цикл модели, включающий не только фазы изменения, претерпеваемые самой моделью, но и “круговорот знаний”, используемых для создания модели и полученных в результате использования модели можно представить в виде схеме, изображенной на рис. 1.