1.Кратні інтеграли

1.1 Подвійні інтеграли

До подвійних інтегралів зводяться задачі про знаходження площ плоских фігур, об’ємів тіл, мас та різних механічних і фізичних характеристик матеріальних об’єктів. Обчислюються подвійні інтеграли зведенням до двохкратних/повторних інтегралів.

Наприклад, якщо треба обчислити 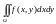, де область інтегрування визначається рівністю

,

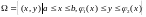тобто область має вигляд

то 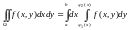. (1.1)

Якщо область D має вигляд

то .

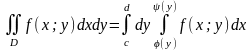Таким чином, для подвійного інтегралу 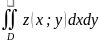від функції по області D існує два способи зведення його до повторного інтегралу в залежності від вибору порядку інтегрування по змінній x та y. Розглянемо правильну область D, тобто, область для якої прямі, паралельні осям координат і що проходять через область D, перетинають її межу γ не більше ніж в двох точках або є частиною межі області D.

І .Спочатку інтегруємо по змінній y, а потім по змінній x. Це означає, що змінна x змінюється в постійних межах: , де a та b – абсциси крайніх точок P та M проекції області D на вісь OX (мал.2.1).

Ці точки розділяють межу γ на дві частини: нижню,що задана рівнянням , та верхню, що задана рівнянням .

мал.2.1

Для отримання меж інтегрування по змінній 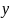роблять так: для 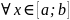проводять пряму AB, паралельну осі OY. Ця пряма перетинає межу γ області D в двох точках A і B. A – точка входу в область D, а B – точка виходу з області D для даного . Точка A лежить на нижній частині межі, що описана рівнянням , а точка B - на верхній частині межі, що описана рівнянням .Отже, для даного 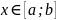змінна змінюється в межах . Таким чином, область D можна записати системою нерівностей

.

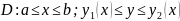Для такого запису маємо формулу зведення подвійного інтеграла до повторного :

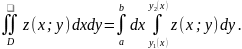(1.2)

В цій формулі обчислення інтегралів відбувається зправа наліво. При цьому, коли обчислюють інтеграл 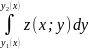, то – вважається сталою. 2.Розглянемо інший порядок інтегрування. С початку інтегруємо по змінній , а потім по змінній .

мал. 2.2 Аналогічні міркування (мал. 2.2) призводять до іншого запису для області D: 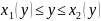. Тому маєму другу формулу зведення подвійного інтегралу до повторного:

(1.3)

В формулі (1.3) при обчисленні змінна вважається сталою. Зауваження1.1:Якщо область D не є правильною, то її розбивають на n правильних під областей, що не перетинаються , , 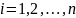так щоб 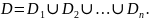За властивістю адитивності подвійного інтегралу маємо 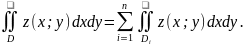Приклад 1.1. Подвійний інтеграл звести до повторного інтегралу, розставивши відповідно межі інтегрування, якщо область обмежена лініями ; (мал.2.3)

мал. 2.3

Розв′язання: Використаємо формулу (1.2). Знайдемо абсциси 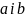точок перетину параболи та нижньої частини півкола 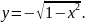Для цього розв′яжемо рівняння 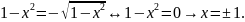Таким чином, змінна змінюється в межах 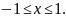Для будь-якого значення змінна змінюється в межах 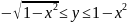Подвійний інтеграл за формулою (1.2) зводиться до повторного інтегралу вигляду Використовуємо формулу (1.3). Змінна змінюється в постійних межах 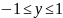(мал.2.4). Межі для змінної знаходять так: для 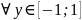знаходять пряму паралельну осі OX. Ця пряма перетинає межу 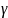в двох точках A, B (мал. 2.4). Проте з мал. 2.4 можна побачити, що для змінної з відрізку 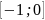межі змінної знаходимо з рівняння : ; .

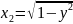мал. 2.4 Для змінної з відрізку 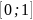змінна знаходимо з рівняння : : ; . В цьому випадку,в силу властивості адитивності подвійного інтегралу, він зводиться до суми двох повторних інтегралів за формулою

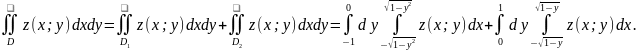
Приклад 1.2. В інтегралі 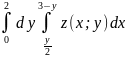змінити порядок інтегрування. Розв′язання: За межами змінних інтегрування записуємо область інтегрування у вигляді нерівності 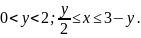Зобразимо цю область графічно (мал. 2.5)

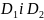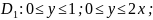
мал.2.5 З мал. 2.5 видно,що при зворотньому порядку інтегрування (спершу по змінній , а потім по змінній ) область необхідно представити у вигляді об′єднання двох областей що не перетинаються . Запишемо цю область у вигляді нерівності 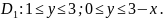Користуючись властивістю адитивності подвійного інтегралу і формулою (1.2) для областей , отримуємо

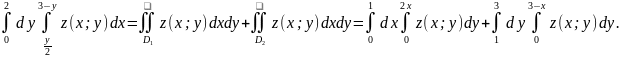
Приклад1.3. Обчислити 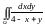, де область обмежена лініями х=0,у=х, .

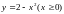Розв′язання: Зазначені лінії за умовою утворюють криволінійний трикутник з вершинами в точках (0;0),(0;2),(1;1), який і відіграє роль області , при цьому .

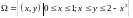Отже,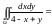

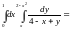
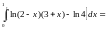
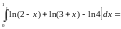
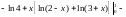
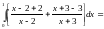
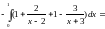
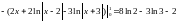
Коли область інтегрування обмежена замкненою лінією 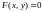, то рівняння лінії визначає у як неявно задану функцію від х. Якщо з рівняння лінії можна знайти у як двозначну функцію від х

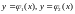
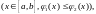
то подвійний інтеграл обчислюється за формулою (1.1).

Приклад 1.4 Знайти площу фігури , обмеженої кривої 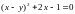та прямою .

Розв′язання: Розв’язуючи рівняння кривої відносно у, маємо , тобто в області інтегрування .

Отже, 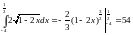(кв.од.)