Лінійна парна регресія

Дані про статистичну залежність зручно задавати у вигляді кореля-ційної таблиці. Розглянемо, як приклад, таблицю залежності між добовим виробітком продукції Y (т) і величиною основних виробничих фондів (ОВФ) Х (млн.грн) для сукупності однотипних виробництв (табл.6.1).

Таблиця 6.1

Величина ОВФ млн.грн (Х)	Середини інтервалів	Добовий виробіток продукції, т (Y)											Всього		Групове середнє, т,( )
		7-11		11-15		15-19		19-23		23-27
	\	9		13		17		21		25
20-25	22,5	2		1		-		-		-		3		10,3
25-30	27,5	3		6		4		-		-		13		13,3
30-35	32,5	-		3		11		7		-		21		17,8
35-40	37,5	-		1		2		6		2		11		20,3
40-45	42,5	-		-		-		1		1		2		23,0
Всього ni			5		11		17		14		3		50		-
Групове середнє млн.грн,			25,5		29,3		37,9		35,4		39,2		-		-

Зобразимо отриману залежність графічно точками координатної площини. Таке зображення статистичної залежності називається полем кореляції. Для кожного значення 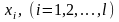, тобто для кожного рядка кореля-ційної таблиці обчислимо групові середні

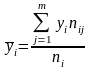, (6.5)

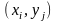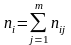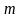де - частоти пар і ; - кількість інтервалів за змінною Y. Обчислені групові середні розташуємо в останньому стовпці кореляційної таблиці і зобразимо графічно у вигляді ламаної, що називається

емпіричною лінією регресії Y по Х (рис. 6.1).

ОВФ, млн.грн

Рис. 6.1

Аналогічно, для кожного значення 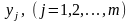обчислимо групові середні (розміщені у нижньому рядку кореляційної таблиці):

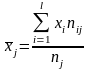, (6.6) де 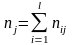, - кількість інтервалів за змінною Х. За виглядом ламаної

лінії можна припустити наявність лінійної кореляційної залежності Y по Х між двома змінними, що розглядаються. Ця залежність графічно буде більш точною, якщо збільшити об’єм вибірки:

. (6.7)

Тому рівняння регресії будемо шукати у вигляді . (6.8)

Параметри рівняння 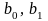знайдемо за методом найменших квадратів, тобто відшукаємо значення мінімізуючи функцію

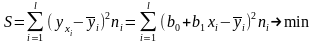(6.9)

Необхідні умови екстремуму:

Після перетворень отримаємо систему нормальних рівнянь для визначення параметрів : (6.10)

Враховуючи формулу (6.5), перетворимо вирази:

.

Поділимо обидві частини нормальних рівнянь на 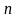і застосуємо формулу (6.7). Отримаємо систему у вигляді:

(6.11)

де , (6.12)

(6.13)

(6.14)

Підставимо значення 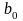з першого рівняння системи (6.11) в рівняння регресії:

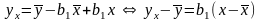(6.15)

Коефіцієнт 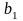називається вибірковим коефіцієнтом регресії Y по Х

( ), отже,

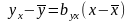(6.16)

Коефіцієнт регресії Y по Х показує, на скільки одиниць в середньому зміниться Y при збільшенні Х на одну одиницю.

Розв’яжемо остаточно нормальну систему і знайдемо :

(6.17)

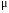де - вибіркова дисперсія змінної Х; - вибірковий кореляційний момент, або вибіркова коваріація.

Розмірковуючи аналогічно, з рівняння регресії Х по Y 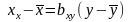матимемо: - вибірковий коефіцієнт регресії Х по Y , що показує, на скільки одиниць в середньому зміниться Х при збільшенні Y на одну одиницю. - вибіркова дисперсія змінної Y. Коефіцієнти регресії 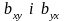мають однакові знаки, що визначаються знаком . Коефіцієнти визначають кутові коефіцієнти відповідних ліній регресії (лінії перетинаються в точці ( )) (див. рис. 6.3).

◄ Приклад 6.1 За даними таблиці 6.1 знайти рівняння регресії Y по Х і Х по Y та пояснити їх зміст.

Розв’язання. Обчислимо всі необхідні суми:

Знаходимо вибіркові характеристики і параметри рівняння регресії:

Отже, рівняння регресії:

З першого рівняння регресії Y по Х випливає, що при збільшенні основних виробничих фондів (ОВФ) Х на 1 млн.грн. добовий виробіток продукції Y збільшиться в середньому на 0,6762 т. Друге рівняння регресії Х по Y показує, що для збільшення добового виробітку продукції на 1 т необхідно в середньому збільшити ОВФ на 0,8099 млн.грн. Зауважимо, що вільні члени рівнянь не мають реального змісту.►