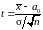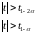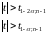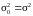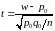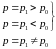Перевірка гіпотез про рівність дисперсій двох сукупностей

Гіпотези про дисперсії виникають достатньо часто, оскільки дисперсія характеризує такі виключно важливі показники, як точність машин, технологічних процесів, пристроїв, степінь однорідності сукупностей, ризик, пов'язаний із відхиленням дохідності активів від очікуваного рівня тощо.

Нехай дано дві нормально розподілені сукупності, дисперсії яких

дорівнюють та 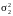. Необхідно перевірити нульову гіпотезу про рівність дисперсій, тобто Н₀: відносно конкуруючої Н₁: або

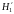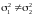: . Для перевірки гіпотези Н₀ із цих сукупностей взято дві неза-

лежні вибірки об’ємом і . Для оцінки дисперсій та використовуються «виправлені» вибіркові дисперсії та . Отже, задача перевірки гіпотези зводиться до порівняння дисперсій та .

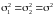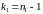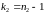При вірності гіпотези Н₀: в якості оцінки можна взяти все ті ж дисперсії та , обчислені по елементах першої та другої вибірок. Вибіркові характеристики і мають розподіл відповідно із і степенями вільності, а їх відношення 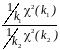має F-розподіл Фішера-Снедекора з і степенями вільності. Таким чином, випадкова величина F, що визначається відношенням

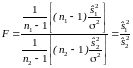, (4.3)

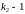тобто відношенням «виправлених» вибіркових дисперсій, має F-розподіл Фішера-Снедекора з і степенями вільності. Вигляд деяких кривих F-розподілу показано на рис. 4.5.

Під час формування критерію відхилення (прийняття) гіпотези Н₀ варто врахувати, що розподіл статистики F (на відміну від нормального або розподілу Стьюдента) є несиметричним. Тому гіпотеза Н₀ відкидається, якщо 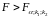(у випадку правосторонньої критичної області — рис. 4.5а), або якщо (у випадку лівосторонньої — рис 4.5б), або якщо або (у випадку двосторонньої критичної області — рис. 4.5в). В протилежному випадку гіпотеза Н₀ не відкидається.

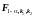
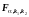
Рис. 4.5

На практиці зазвичай використовується таблиця значень

F-критерію, в якій подано значення і . Це дозволяє

здійснювати перевірку гіпотези Н₀ на 5%-вому на 1%-вому рівнях значущості при використанні односторонньої критичної області, та на 10%-вому і 2%-вому рівнях значущості при використанні двосторонньої критичної області.

Перевірка гіпотез про числові значення параметрів

Гіпотези про числові значення зустрічаються у різноманітних задачах.

В загальному випадку гіпотези такого типу мають вигляд Н₀: θ = Δ₀, де θ — деякий параметр розподілу, що досліджується, а Δ₀ — область його конкретних значень, що в частковому випадку складається із одного значення. Під час перевірки гіпотези вказаного типу можна використовувати той же підхід, що і раніше. Відповідні критерії перевірки гіпотез про числові значення параметрів нормального закону надані в табл. 4.1.

◄ Приклад 4.5 На основі зробленого прогнозу середня дебіторська заборгованість однотипних підприємств регіону повинна скласти а₀ = 120 грош. од. Вибіркова перевірка 10 підприємств дала середню заборгованість x = 135 грош. од., а середнє квадратичне відхилення заборгованості s = 20 грош. од. На рівні значущості 0,05: а) визначити, чи можна прийняти даний прогноз; б) знайти потужність критерію, використаного в п.а); в) знайти мінімальне число підприємств, яке варто перевірити, щоб забезпечити потужність критерію 0,975.

Розв’язання. а) Гіпотеза, що перевіряється, Н₀: . Альтернативна - гіпотеза Н₁: . Оскільки генеральна дисперсія σ² невідома, то використаємо t-критерій Стьюдента. Статистика критерію у відповідності до табл. 4.1 дорівнює 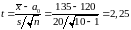. Критичне значення статистики . Оскільки 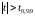(2,25 > 1,83), то гіпотеза Н₀ відкидається, тобто на 5%-вому рівні значущості зроблений прогноз повинен бути відкинутий.

б) Оскільки a₁=135>a₀=120, то критична область правостороння і критичне значення вибіркового середнього

(грош. од.). Тобто критична область значень для x — інтервал (132,2;+∞).

Потужність критерію дорівнює ,

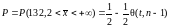де — функція, що виражає ймовірність попадання випадкової величини, яка має t-розподіл Стьюдента, на відрізок (-t, t)

.

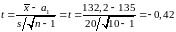За таблицею:

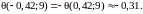
Отже, .

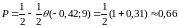в) Скористаємось розв’язком прикладу 4.1 б). Оскільки у нас σ² невідома, а відома лише її вибіркова оцінка s², то статистика критерію 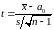має t-розподіл Стьюдента (див. табл. 4.1), і відповідна скорегована формула для n прийме вигляд: . При α=0,05, β=0,025 (тому що за умовою потужність критерію 1-β=0,975), а₀=120, а₁=135, s=20 отримаємо: . Оскільки права частина рівності сама залежить від невідомого значення n, то n знаходиться наближено підбором. 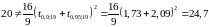Так, при n=20, n=30, рівність не виконується (наприклад, при n=20 ), а при n=25 .

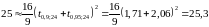Таким чином, необхідно перевірити 25 підприємств.►

Таблиця 4.1

Нульова гіпотеза	Припущення	Статистика критерію	Альтернативна гіпотеза	Критерій відхилення гіпотези
а = а0	σ2 відома
	σ2 невідома
	а невідомо			або
p=p0	n достатньо велике

Аналогічно перевіряються і інші гіпотези про числові значення параметрів у відповідності до критеріїв перевірки, наведених у табл. 4.1.