2.3 Модель sir

2.3.1 Теоретические сведения

Для оценки факторов, обеспечивающих затухание сетевых эпидемий, можно использовать SIR-модель (“Susceptible–Infected–Removed model”). В ней хосты существуют в трех состояниях: уязвимом (S), зараженном (I) и невосприимчивом (R). Таким образом, S+I+R=N[3].

Предположим, что узлы оказываются неуязвимыми только после излечения от инфекции.

Таким образом, в результате функционирования модели узлы будут либо невосприимчивыми, либо неуязвимыми.

Модель характеризуется следующими этапами:

1) медленное возрастание количества инфицированных узлов (приблизительно до уровня 1-2% от доли всех узлов). Этап длится малое время.

2) более резкое возрастание количества инфицированных узлов (крутизна графика зависимости доли инфицированных узлов от времени зависит от вероятности заражения). Время возрастания инфицированных узлов происходит до тех пор, пока не пройдёт время инфицирования большинства узлов, и при этом доля восприимчивых узлов будет достаточно малой, по сравнению с начальным значением (происходит «насыщение» инфицированными узлами).

3) Этот этап характеризуется резким возрастанием количества неуязвимых узлов, а также резким убыванием количества инфицированных узлов.

2.3.2 Аналитическое описание модели SIR

Вводя постоянную среднюю скорость «иммунизации» в единицу времени γ и учитывая, что i=I/N, r=R/N, s=S/N, получаем систему уравнений[3]:

(9)

В этой модели вводится понятие порогового условия для развития эпидемии. На участке возрастания i(t) производная 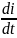должна быть больше 0. Поскольку s(t) непрерывно уменьшается за счет инфицированных машин, то получаем, что для начала эпидемии необходимо выполнение следующего условия[3]:

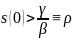
(10)

Выполнение этого условия достигается легко: поскольку γ определяется запаздывающей человеческой реакцией и необходимостью загрузки громоздких «заплат», а β — постоянно улучшающимися техническими характеристиками сети и возможностями злоумышленника. Например, злоумышленник может вставить небольшую паузу в цикл размножения, чтобы не создавать катастрофического трафика, и слегка понизить скорость инфицирования.

Доля же уязвимых узлов обычно очень велика. Поэтому практически всегда β значительно превосходит γ . Например, при моделировании эпидемии Code Red v2 в [8] соответствие с реальными данными достигнуто при соотношении [3].

2.3.3 Описание алгоритма функционирования модели SIR в заданной сети

Для функционирования модели необходимо случайным образом распределить инфекционные узлы. Затем в цикле вызывается функция, в которой производится процесс вероятностного заражения и восстановления узлов сети. Внутри этого же цикла производится отсчёт времени, равный периоду.

Функция расчёта состояния узлов, упомянутая выше, работает ниже приведённым образом. В функцию передаются в качестве параметров: скорость взаимодействия узлов между собой (число контактов за период), вероятность заражения восприимчивого узла при взаимодействии с инфицированным узлом, время восстановления инфицированного узла (переход из инфицированного состояния в неуязвимое). Также в функцию передаётся количество инфицированных, неуязвимых и восприимчивых узлов на данный момент. Далее производится поиск инфицированного узла, который случайным образом взаимодействует с другими узлами. Факт взаимодействия с узлом или отсутствие этого взаимодействия носит вероятностный характер. Число таких взаимодействий ограничено числом связей инфицированного узла, а также числом взаимодействий за период. Далее производится заражение восприимчивого узла с вероятностью, переданной в качестве параметра. Если восприимчивый узел был инфицирован, то запоминается время его инфицирования. Далее производится проверка, не прошло ли время восстановления для каждого инфицированного узла. Если это время прошло, то инфицированный узел становится неуязвимым.

2.3.4 Блок-схема алгоритма функционирования модели SIR в заданной сети