Замечания руководителя

СОДЕРЖАНИЕ

1 ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ 4

1.1 Цель и задачи работы 4

2 ОСНОВНОЕ СОДЕРЖАНИЕ 7

2.1 Безмасштабные сети 7

2.2 Модель SI 18

2.2.1 Теоретические сведения 18

2.3 Модель SIR 26

2.3.1 Теоретические сведения 26

2.4 Модель SEIR 33

2.4.1 Теоретические сведения 33

SEIR-модель (“Susceptible–Exposed–Infected–Removed model”), являющаяся модификацией SIR–модели. В этой модели учитывается возможность того, что червь может иметь некий «инкубационный период», во время которого вирус не наносит какого-либо вреда инфицированному узлу. Обычно червь заражает уязвимый узел (S) до входа в свою латентную стадию. В течение латентного периода (Е, Exposed) узел считается зараженным, но не распространяет вирус. Через некоторое время он становиться способным к заражению других хостов (I) и далее становиться «излеченным» (R). В SEIR-модели требуется дополнительно вводить соотношение, характеризующее отношение между состояниями E и I.[1] 33

2.5 Модель SAIR 40

2.5.1 Теоретические сведения 40

2.6 Модель PSIDR 54

2.6.1 Теоретические сведения 54

ЗАКЛЮЧЕНИЕ 66

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 67

1 Общая характеристика работы

1. Цель и задачи работы

Целью настоящей работы является создание программного комплекса анализа и моделирования деструктивных воздействий в безмасштабных сетях

Поставленная цель обуславливает необходимость решения следующих задач:

1. Реализация возможности построения (генерации) социальных графов (модели SI/SIR/SEIR/SAIR/PSIDR);

2. Разработка функционала для нахождение основных статистических величин исследуемой сети;

3. Разработать функционал для проведения эпидемиологических исследований и расчетов.

1.2 Практическая значимость разработки

Данная программа позволяет генерировать случайным образом безмасштабную сеть. На её основе производится симуляция эпидемии на основе следующих моделей: SI, SIR, SEIR, SAIR, PSIDR. Для каждой из этих моделей строятся графики, причём построение происходит во всё время функционирования модели. При окончании моделирования можно вновь запустить симуляцию в той же сети. Графики старой симуляции не стираются, что позволяют производить сравнительный анализ развития эпидемий при различных параметрах и различных моделях развития эпидемии. Весь функционал программы позволяет исследовать, с помощью симуляции, развитие эпидемии, а также демонстрировать ход симуляции при помощи графиков и рисунка сгенерированной сети (ход симуляции отражается на цвете узлов сети, в зависимости от его состояния).

2 Основное содержание

2.1 Безмасштабные сети

Наиболее значительные результаты последних лет в изучении сетевых структур были получены в теоретической физике. В частности в 1999 г. появилась теория безмасштабных сетей, сформулированная Альбертом-Лассо Барабаши. Безмасштабные сети – это граф, где распределение числа связей вершин описывается степенным, а не экспоненциальным (как в пуассоновских сетях) законом, кроме того, объекты, распределенные по степенному закону, нередко устроены иерархически, а основные свойства сети не зависят от размера сети. Название не было придумано специально для этого типа сетей, а было взято из теории критических явлений, где флуктуации в критических состояниях также подчиняются степенному закону, а саму теорию безмасштабных сетей стали рассматривать как один из сценариев выхода сложных систем в критическое состояние. Исследования показали, что большинство сетей в живой и неживой природе (информационные, экологические, генные, функциональные связи в мозге человека, метаболические, социальные, технологические, словарные, документы WWW и др.) хорошо моделируются безмасштабными графами. По мнению крупнейшего социолога, профессора Калифорнийского университета Мануэля Кастельса, все общество в целом становится «сетевым», что происходит благодаря качественно новым средствам коммуникации. «...Новая коммуникационная система, все более говорящая на универсальном цифровом языке, одновременно интегрирует в глобальном масштабе производство и распространение слов, звуков и изображений в нашей культуре и приспосабливает их к персональным вкусам и настроениям индивидов. Интерактивные компьютерные сети растут по экспоненте, создавая новые формы и каналы коммуникации, формируя жизнь и формируясь жизнью в одно и тоже время» (Кастельс, 2000). В работе «Галактика Интернет: Размышления об Интернете, бизнесе и обществе» исследователь отмечает [9]: «вообще-то сети – это достаточно старые формы материализации человеческой деятельности, однако в наши дни они обрели новую жизнь в результате превращения их в информационные сети, объединенные Интернетом». Центральным понятием теории М. Кастельса становится «сетевая структура», раскрывающаяся как «комплекс взаимосвязанных узлов», при этом «конкретное содержание каждого узла зависит от характера той конкретной сетевой структуры, о которой идет речь» [7]. Связь определяется через способность к коммуникации. Сами «сети представляют собой открытые структуры, которые могут неограниченно расширяться путем включения новых узлов, если те способны к коммуникации…» [7]. Включенность в сеть обеспечивает доступ к информации [8]. В работах ученого впервые дается теоретическое обоснование наличия сетевой логики в социальных процессах и явлениях[10].

2.1.2 Математическое описание безмасштабных сетей

Устойчивость сетевой архитектуры является одной из важнейших проблем построения эффективных сложных социальных, биологических, технических и других систем. Стоит обратить внимание, что для ряда сложных систем характерна высокая численность элементов, которая может достигать десятков и сотен тысяч, и нерегулярность связей. Таким системам и их сетевым моделям, обладающим нетривиальными топологическими свойствами, в наибольшей степени отвечает термин «комплексные». Наиболее популярными и отвечающими реальности комплексными сетями в настоящее время являются модели Эрдёша–Реньи и Барабаши–Альберта. В первой плотность распределения связей отвечает закону Пуассона[6]:

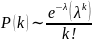
(1)

Эти сетевые модели также носят название случайных или экспоненциальных (Е-сети). Во второй половине XX в. экспоненциальные сети являлись базовыми для анализа систем. С такого рода моделями связано развитие теории графов. В 1998 г. в своей основополагающей работе А.-Л. Барабаши (Albert Laslo Barabasi) с сотрудниками обратил внимание исследователей на то, что многие реальные сети (коммуникационные, веб-, социальные и метаболические) носят иной, нежели описываемые экспоненциальной моделью, характер. Авторами была предложена сетевая модель, в которой:

1) распределение связности (числа связей, или степени) отвечает степенному закону[6]:

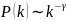
(2)

2) характеристикой является рост сети с введением новых узлов и новых связей, причем наблюдается так называемое предпочтительное присоединение;

3) использована терминология, простая и понятная для специалистов различных дисциплин. Такая модель сети носит название безмасштабной (SF)[6].

Стоит отметить, что есть и более точная формула для закона распределения связности в безмасштабных сетях:

(3)

В формуле (3) с=const – нормировочная постоянная.

2.1.3 Описание алгоритма формирования случайной безмасштабной сети

Генерация безмасштабной сети производится с помощью функции, которая будет возвращать массив (матрицу смежности), элементы которого:

(4)

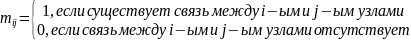
Так как граф неориентированный, то матрица M – симметричная.

Для создания такой матрицы необходимо передать параметр характеризующий сеть – параметр 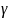. Далее для генерации, согласно формуле (), потребуется параметр c, который высчитывается согласно условию нормировки (сумма долей узлов должна равняться единице).

Для расчёта параметра c необходимо просуммировать все доли узлов, имеющих связность k. Вернуть необходимо значение , где n – количество узлов сети.

Далее, в функции генерации безмасштабной сети, необходимо задать массив, величиной n-1 элементов, где в i-ом элементе массива хранится количество узлов, имеющих связность k. Затем формируется массив в n элементов, в котором хранится, количество связей i-го элемента. Равномерно распределяем в этот массив узлы с k связями. Затем переходим к формированию требуемой матрицы. Для формирования этой матрицы необходимо связи i-го узла (количество которых хранится в массиве), равномерно распределить на другие n-1 узлов. В итоге на выходе получится массив (матрица), описывающий сгенерированную безмасштабную сеть.

2 .1.4 Блок-схема алгоритма генерации случайной безмасштабной сети

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3