Тема 8. Произвольная плоская система сил

8.1. Приведение плоской системы сил

Рассмотрим случай приведения к заданному центру сил, произвольно расположенных на плоскости.

Рис. 8.1

Пусть к твердому телу приложены силы , лежащие в одной плоскости и приложенные соответственно в точках (рис. 8.1,а).

Примем за центр приведения некоторую точку , лежащую в этой плоскости и приведем все силы к этому центру. В результате приведения получим систему сходящихся сил , приложенных в центре и лежащих в одной плоскости, а также систему присоединенных пар, алгебраические моменты которых равны (рис. 8.1,б).

Сложив сходящиеся силы, получим главный вектор системы сил , который будет лежать в той же плоскости, что и вся система. Как известно, главный вектор системы представляется замыкающим вектором многоугольника построенного из векторов 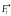, геометрически равных силам заданной системы (рис. 8.1,в).

Моменты присоединенных пар равны моментам сил системы относительно центра приведения, то есть

Сложив алгебраические моменты всех сил системы относительно точки О, получим алгебраический главный момент системы сил относительно точки О.

Таким образом (рис. 8.1,г),

силы, произвольно расположенные на плоскости, можно привести к одной силе, приложенной в центре приведения, равной главному вектору данной системы сил, и к лежащей в той же плоскости паре сил с алгебраическим моментом, равным главному алгебраическому моменту системы сил относительно центра приведения.

То есть

.

Выбор центра приведения не отражается на модуле и направлении главного вектора, но влияет на величину и знак главного момента.

8.2. Частные случаи приведения плоской системы

Итак, любая плоская система сил может быть заменена

• одной силой (равной главному вектору системы сил и приложенной в центре приведения О) и/или

• одной парой (с алгебраическим моментом, равным главному алгебраическому моменту си­стемы сил относительно центра приведения ).

Однако в ряде случаев и эту систему сил можно упростить.

Рассмотрим эти случаи.

1. Если и , то система сил уравновешена (эквивалентна нулю).

2. Если и , то система сил эквивалентна одной паре сил.

3. Если и , то система сил эквивалентна одной силе, т. е. имеет равнодействующую, которая проходит через центр приведения О.

4. Если и (имеются и сила и пара), то система сил оказывается эквивалентной одной силе , т. е. имеет равнодействующую равную главному вектору, которая не проходит через центр приведения О.

Рис. 8.2

Рассмотрим последний случай (рис. 8.2).

Так как элементы пары можно изменять, сохраняя при этом ее момент, расположим пару , момент которой равен главному моменту системы сил следующим образом:

1. пусть одна из сил пары ( ) будет приложена в точке О и направлена против силы (рис. 8.2, б);

2. пусть модули сил, составляющих пару, равны модулю главного вектора: , и тогда плечо пары будет равно .

Уравновешенную систему сил и можно исключить.

Исходная система сил оказывается эквивалентной одной силе , т. е. имеет равнодействующую (равную главному вектору), линия действия которой проходит на расстоянии от центра О.