2. Простейшие способы интегрирования.

а) Непосредственное интегрирование.

Нахождение интегралов функций, основанное на прямом применении свойств неопределенных интегралов и таблицы основных формул интегрирования. Рассмотрим пример нахождения интеграла функции путем непосредственного интегрирования.

Пример:

∫(х –3)²dх = ∫(х²–6х+9)dх = ∫х²dх- 6∫хdх+9∫dх = х³∕3 -3 х²+9х+С.

В подавляющем большинстве случаев мы имеем дело с интегралами функций, которые нельзя найти непосредственным интегрированием. В этом случае необходимо сделать подстановку (заменить переменную).

б) Интегрирование подстановкой (замена переменной).

Интегрирование подстановкой, или как его часто называют, методом замены переменой, является одним из более эффективных и распространенных методов интегрирования. Способ подстановки состоит в том, чтобы перейти от данной переменной интегрирования к другой переменной с целью упростить подинтегральное выражение и привести его к одному из табличных видов интегралов. При этом выбор подстановки решается исполнителем индивидуально, т.к. не существует общих правил, указывающих какую подстановку в данном случае взять.

Пример: Найти интеграл ∫е^2х+3dх.

Введем новую переменную t, связанную с х следующей зависимостью 2х + 3 = t.

Возьмем дифференциалы от левой и правой частей этого равенства: 2dх = dt; dх =dt/2.

Теперь вместо 2х + 3 и dх в подинтегральное выражение подставим их значения. Тогда получим: ∫е^2х+3dх = ∫е^tdt = е^t + С. Возвращаясь к прежней переменной, получим окончательно выражение:

∫е^2х+3dх = е^2х+3 + С.

Чтобы убедиться в правильности взятия интеграла необходимо первообразную функцию е^2х+3 продифференцировать и проверить, будет ли ее производная равна подинтегральной функции:

( е^2х+3)' = е^2х+3 · (2х+3)' = е^2х+3.

3. Определенный интеграл и его свойства.

Понятие определенного интеграла широко используется во многих областях науки и техники. С его помощью вычисляются площади, ограниченные кривыми, объемы произвольной формы, мощность и работа переменной силы, путь движущегося тела, моменты инерции и многие другие величины.

В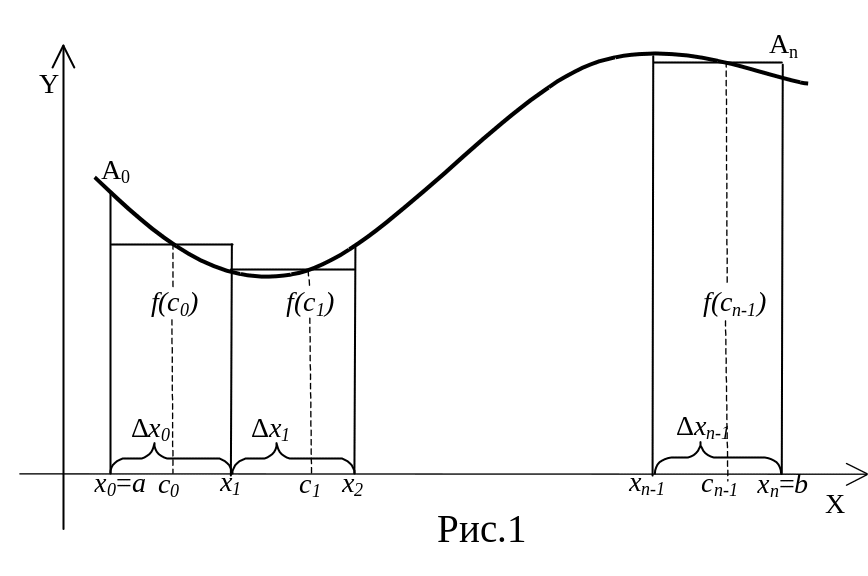 подавляющем большинстве случаев понятие определенного интеграла вводится при решении задач определения площади криволинейной трапеции. Пусть имеется непрерывная функция у = f(х) на отрезке [а,в]. Фигуру, ограниченную кривой у= f(х) ординатами аА_{о ,} вА_п и отрезком [а,в] оси абсцисс называют криволинейной трапецией (рис.1).

Поставим перед собой задачу: определить площадь S криволинейной трапеции аА_оА_пв. Для этого разобьем отрезок [а,в] на п не обязательно равных частей и обозначим точки деления таким образом: а = х_о‹ х₁‹ х₂ ‹ … ‹х_п = в .

Из точек деления восстановим перпендикуляры до пересечения с кривой у = f(х). Таким образом, мы всю площадь, ограниченную кривой, разбили на п элементарных криволинейных трапеций. Восстановим из произвольных точек каждого отрезка ∆х_i ординаты f(С_i) до пересечения с кривой у = f(х). Далее построим ступенчатую фигуру, состоящую из прямоугольников с основанием ∆х_i и высотой f(С_i). Элементарная площадь i-го прямоугольника будет S_i = f(С_i)(х_i - х_i-1), а вся площадь S_п полученной ступенчатой фигуры будет равна сумме площадей прямоугольников:

S_п = f(С_о)(х₁ –х_о) + f(С₁)(х₂ –х₁ ) + … + f(С_п-1)(х_п –х_п-1).

Для сокращения записи этой суммы вводят символ (сигма) – знак, означающий суммирование величин. Тогда

S_п = .

Эта сумма S_{п ,} которая называется интегральной суммой, может быть или больше или меньше истинного значения данной площади. Наиболее близким значением к истинной величине площади будет предел суммы при условии, что элементарные отрезки будут дробиться (п→ ), а длина самого большого отрезка ∆х_max будет стремиться к нулю, т.е.:

S = (4)

Этот предел интегральной суммы (если он существует) называется определенным интегралом от функции f(х) на отрезке [а,в] и обозначают: = (5)

(читается – “определенный интеграл от а до в эф от икс дэ икс”).

Числа а и в называются соответственно нижним и верхним пределами интегрирования, f(х) – подинтегральной функцией; х – переменной интегрирования. Применив формулы (4) и (5) можно записать. Что площадь криволинейной трапеции численно равна интегралу от функции, ограничивающей трапецию, взятому на интервале интегрирования [а,в]:

.

Этот факт выражает геометрический смысл определенного интеграла.

Рассмотрим свойства определенного интеграла.

1. Определенный интеграл не зависит от обозначения переменной, т.е.: = .

2. Определенный интеграл алгебраической суммы равен алгебраической сумме определенных интегралов от каждого слагаемого:

[f₁(х) + f₂(х) + … dх] = f₁(х) dх + f₂(х) dх + ….

3. Постоянный множитель к в подинтегральном выражении выносится за знак интеграла:

кf(х) dх = к f(х) dх.

4. Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл изменит свой знак на противоположный, сохранив абсолютную величину неизменной:

f(х) dх = - f(х) dх.

5. Если отрезок [а,в] разбить на две части [а,с] и [с,в] , то интеграл:

f(х) dх = f(х) dх + f(х) dх.

6. dх = в – а, при а ≠ в . Это свойство вытекает из того, что неопределенный интеграл ∫ dх = х, т.е. равен некоторой длине отрезка, началом и концом которой будут точки а и в этого отрезка.

7. Если подинтегральная функция на отрезке [а,в] сохраняет постоянный знак, то и определенный интеграл будет представлен числом того же знака, т.е.: f(х)>0 и f(х) dх>0.

Существуют и другие свойства определенного интеграла, которые мы рассматривать не будем.