2. Производная сложной функции.

Функция является сложной, если она может быть представлена в виде функции от функции у = f[φ(х)], где у = f(u), а u = φ(х), где u  промежуточный аргумент. Любую сложную функцию можно представить в виде элементарных функций (простых), которые являются ее промежуточными аргументами.

Примеры:

Простые функции: Сложные функции:

у= х² у = (х+1)²; u = (х+1); у= u²;

у = sin x; у = sin 2x; u = 2х; у = sin u;

у = е^х у = е^2х; u = 2х; у = е^u;

у = ln х у = ln (х+2); u = х+2; у = ln u.

Общее правило дифференцирования сложной функции дается приведённой теоремой без доказательства.

Если функция u = φ(х) имеет производную u'_x = φ'(х) в точке х, а функция у = f(u) производную у'_u = f'(u) в соответствующей точке u, то производная сложной функции у = f[φ(х)] в точке х находится по формуле: у'_х = f'(u) · u'(х).

Часто используется менее точная, но более короткая формулировка данной теоремы: производная сложной функции равна произведению производной по промежуточной переменной на производную промежуточной переменной по независимой переменной.

Пример: у = sin 2x²; u = 2х²; у = sin u;

у'_х = (sin u)'_u · (2x²)'_х = cos u · 4х = 4х · cos 2х².

3. Производная второго порядка. Механический смысл второй производной.

Производную функции у =f(х) называют производной первого порядка или просто первой производной функции. Эта производная является функцией от х и её можно дифференцировать вторично. Производная от производной называется производной второго порядка или второй производной. Она обозначается: у"_хх – (игрек два штриха по икс); f"(х) – (эф два штрих по икс); d²у/dх² – (дэ два игрек по дэ икс дважды); d²f/dх² – (дэ два эф по дэ икс дважды).

Исходя из определения второй производной, можно записать:

у"_хх = (у'_х)'_х; f"(х) = [f'(х)]'_x d²у/dх² = d/dх (dу/dх).

Вторая производная в свою очередь есть функция от х и ее можно дифференцировать и получить производную третьего порядка и т.д.

Пример: у = 2х³+х²; у"_хх = [(2х³+х²)'_x]'_x = (6х²+2х)'_x = 12х+2;

Механический смысл второй производной объясняется на основе мгновенного ускорения, которым характеризуют переменное движение.

Если S = f(t) – уравнение движения, то  = S'_t; а_ср. = ;

а_мгн.= а_ср = = '_t; а_мгн. = '_t = ( S'_t)'_t = S"_tt .

Таким образом, вторая производная от пути по времени равна мгновенному ускорению переменного движения. В этом и заключается физический (механический) смысл 2-ой производной.

Пример: Пусть прямолинейное движение материальной точки происходит по закону S =t³/3. Ускорение материальной точки будет определяться как вторая производная S"_tt: а = S"_tt = (t³/3)" = 2t.

4. Дифференциал функции.

С понятием производной тесно связано понятие дифференциала функции, которое имеет важное практическое применение.

Функция f(х) имеет производную = f'(х);

Согласно теореме (теорему не рассматриваем) о связи бесконечно малой величины α(∆х)( α(∆х)=0) с производной: = f'(х)+ α (∆х), откуда ∆f = f'(х) ∆х+α(∆х) · ∆х.

Из последнего равенства следует, что приращение функции состоит из суммы, каждое слагаемое которой есть бесконечно малая величина при ∆х→ 0.

Определим порядок малости каждой бесконечно малой величины этой суммы по отношению к бесконечно малой ∆х:

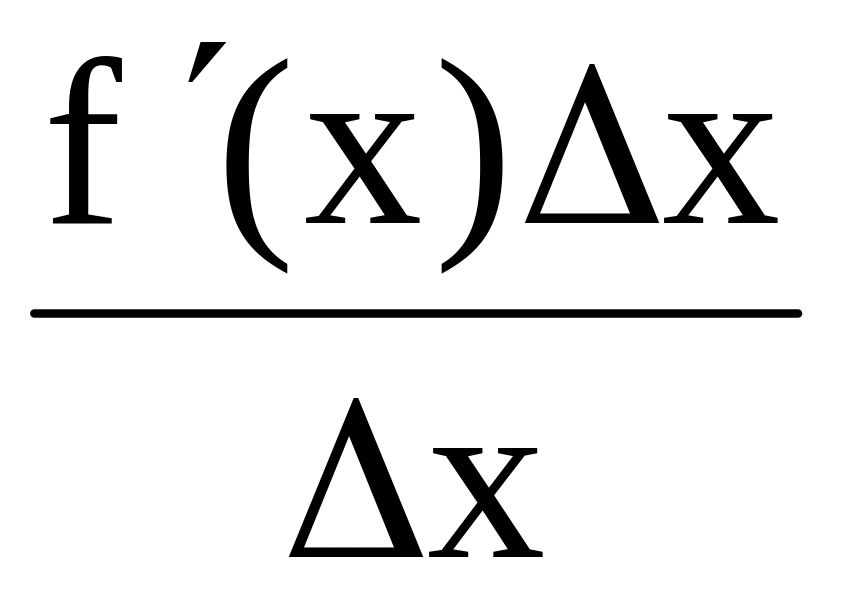1. = f'(х) = const.

Следовательно, бесконечно малые f (х) ∆х и ∆х имеют одинаковый порядок малости.

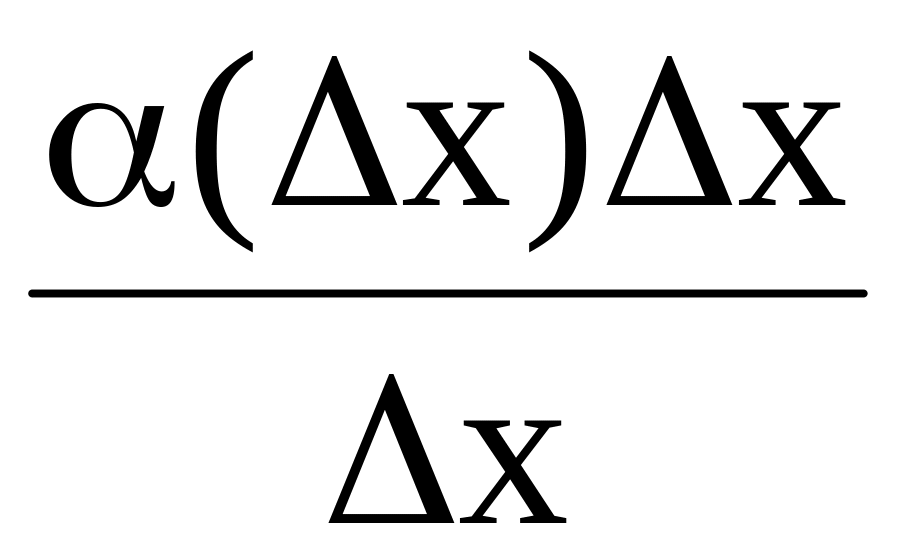2. = α(∆х) = 0.

Следовательно, бесконечно малая величина α(∆х)∆х имеет более высокий порядок малости по отношению к бесконечно малой величине ∆х. Это означает, что в выражениях для ∆f второе слагаемое α(∆х)∆х быстрее стремится к 0 при ∆х→0, чем первое слагаемое f'(х)∆х.

Это первое слагаемое f'(х)∆х называют дифференциалом функции в точке х. Он обозначается dy (дэ игрек) или df (дэ эф). Итак,dy=df= f'(х)∆х или dy = f'(х) dх, т.к. дифференциал dх аргумента равен его приращению ∆х (если в формуле df = f'(х)dх принять, что f(х)=х, то получим df = dx = x'_х∆x, но x'_х =1, т.е. dx =∆х). Итак, дифференциал функции равен произведению этой функции на дифференциал аргумента.

Аналитический смысл дифференциала заключается в том, что дифференциал функции – есть главная часть приращения функции ∆f, линейная относительно аргумента ∆х. Дифференциал функции отличается от приращения функции на бесконечно малую величину α(∆х)∆х более высокого порядка малости, чем ∆х. Действительно ∆f=f'(х)∆х+α(∆х)∆х или ∆f = df +α(∆х)∆х; откуда df = ∆f - α(∆х)∆х.

Пример: у = 2х³ +х²; dу =? dу = у'dх = (2х³+х²)'_xdx = (6х² +2х)dx.

Пренебрегая бесконечно малой величиной α(∆х)∆х более высокого порядка малости, чем ∆х, получим df ≈ ∆f ≈ f'(х)dх т.е. дифференциал функции может быть использован для приближенного вычисления приращения функции, так как дифференциал обычно вычислять проще. Дифференциал может быть применен и к приближенному вычислению значения функции. Пусть нам известна функция y = f(х) и ее производная в точке х. Необходимо найти значение функции f(х+∆х) в некоторой близкой точке (х+∆х). Для этого воспользуемся приближенным равенством ∆у ≈ dy или ∆у ≈ f'(х) · ∆х. Учитывая, что ∆у=f(х+∆х)-f(х), получим f(х+∆х)-f (х) ≈ f'(х) · dх, откуда f(х+∆х) = f(х)+f'(х) · dх. Полученная формула решает поставленную задачу.