Теория технических систем

Тема №1

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ТЕХНИЧЕСКИХ СИСТЕМ

1. Системный подход, определение систем.

2. Виды систем.

3. Основные задачи системного анализа.

1.Системный подход, определение систем

Теория технических систем сформировалась как самостоятельная наука во второй половине 20 столетия. Наиболее весомый вклад в ее развитие внесли Бусленко Н. П., Гальперин И. И., Саркисян С. А., Болтянский В. Г. и другие ученые. Сегодня теория систем является методологической наукой, определяющей принципы и методы анализа, управления и синтеза систем. По данным Соломенцева Ю.М. только владение системными методами анализа, исследования, проектирования позволяет достичь реальных результатов в науке и технике.

В переводе с греческого (systема) это - целое, составное из частей. Сегодня под системой понимают множество элементов, находящихся в отношениях и связях с друг с другом.

Для систем характерно:

1. Иерархичность структуры. Каждая из систем может расчленяться на отдельные подсистемы, которые в свою очередь могут рассматриваться как совокупность отдельных подсистем и элементов. Система может также являться подсистемой более крупной системы. Например, автомобиль состоит из отдельных агрегатов и узлов (подсистем) и одновременно может рассматриваться в качестве подсистемы автотранспортного предприятия.

2. Наличие связей между элементами, превосходящими по мощности связи этих элементов с элементами, не входящими в систему.

3. Наличие интегрированных качеств. Например, простая совокупность деталей автомобиля (станка), не объединенных должным образом, свойствами автомобиля (станка) не обладает.

4. Наличие пространственно-временных характеристик. Каждая система имеет свой календарь и историю развития. Например, параметры состояния автомобиля изменяются от момента начала эксплуатации до момента списания, когда система прекращает свое существование.

Сущность системного подхода заключается в том, что некоторая область материального мира разбивается на 2 части, одна из которых рассматривается как система, вторая - как окружающая среда. Обязательным условием такого выделения является учет связей системы с окружающей средой. Без связей со средой система мертва. Так, например, автомобиль может перемещаться только в среде, станок не может выдавать обработанные детали, если на него не поступают заготовки и энергия. Все связи системы со средой принято разделять на входные переменные, управляющие воздействия, выходные переменные, возмущающие воздействия. Кроме того, сама система характеризуется совокупностью параметров состояния , рис.1.

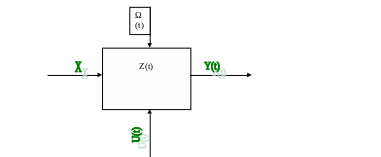
Рис.1 Связи системы с окружающей средой.

На рис.1 входные переменные обозначены вектором . К ним отнесены такие, которые поступают из среды на техническую систему и при работе системы в заданный промежуток времени остаются неизменными. Примерами входных переменных являются параметры настройки станка, которые не меняются при обработке одной детали. Вектором

U(t)=(u₁(t),u₂(t),…,u_r(t)) обозначено управляющее воздействие, представляющее собой совокупность входных переменных, которые изменяются в процессе работы системы по заданному закону. К таким переменным, например, относится поперечная подача при круглом наружном шлифовании, которая изменяется за период обработки одной поверхности. Основная часть припуска удаляется при большей подаче, в конце обработки подача уменьшается. За счет такого изменения подачи обеспечивается высокое качество детали при высокой производительности процесса. Наличие вектора управления в значительной степени расширяет эксплуатационные свойства технической системы. Вектор Ω(t), рис. 1, объединяет неконтролируемые, случайно изменяющиеся переменные, поступающих из среды на систему, а также случайные отклонения от заданных значений составляющих векторов X и U. В среду от системы поступают выходные переменные, которые обозначены на рис.1 вектором Y(t)=(y₁(t),y₂(t),…,y_r(t)). Состояние системы в любой момент времени характеризуется совокупностью параметров состояния Z(t)=(z₁(t),z₂(t),…,z_k(t)), которые могут изменяться в процессе работы системы.