Задание 4
По известной расчетной зависимости косвенного метода измерения и по известным результатам и погрешностям прямых измерений получить формулы и рассчитать предельную δyпр и среднеквадратичную δyск оценки погрешности косвенного измерения. Исходные данные приведены в таблице 4.
Таблица 4. Исходные данные
№ варианта |
Расчетная зависимость |
Погрешности и результаты прямых измерений |
||||
A |
B |
C |
D |
E |
||
2 |
Y = 1/[A(B-C)D2E] |
∆A = 1 A = 100 |
∆B = 2 B = 80 |
∆C = 1 C = 60 |
∆D = 2 D = 40 |
∆E = 1 E = 20 |
Решение
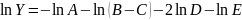
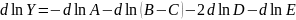
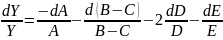
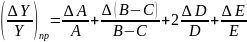
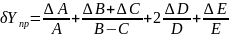
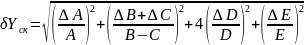
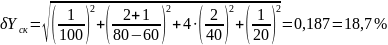
Задание 5
Вариант 2
1.
Постоянный ток в ветви электрической
цепи с сопротивлением R
= 20кОм измерен с помощью амперметра
класса точности 1,5 с пределом измерения
10мкА и внутренним сопротивлением 1,5кОм.
Измеренное значение тока Ĩ = 4,0 мкА.
Рассчитать инструментальную погрешность
и погрешность согласования. Внести
поправку и записать результат измерения.
Решение
Класс
точности амперметра задан числом с
кружочком, следовательно, относительная
погрешность, выраженная в процентах,
во всех точках шкалы не должна превышать
по модулю класса точности, т.е.
.
При
рассмотрении худшего случая получаем
относительную погрешность
.
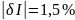Погрешность согласования
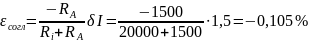
Определяем абсолютную поправку на измерение напряжения
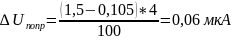
Результат измерения
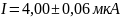
2. Какой амперметр следует выбрать для измерения тока в диапазоне от 3А до 5А с относительной погрешностью не более 0,3%? Характеристики приборов приведены в таблице 1.
Таблица 1
Класс точности, % |
Предел измерения, А |
0,1/0,05 0,2 0,2 |
10 5 10 |
Решение
Первый амперметр. Класс точности первого амперметра задан в виде двух чисел, разделенных косой чертой. Следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы должна удовлетворять следующему соотношению:
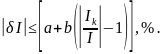
В
данном случае
;
;
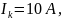причем параметры этой формулы
и
ответственны, соответственно, за
мультипликативную и аддитивную
составляющие суммарной погрешности.
Таким образом, получаем
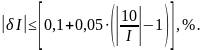
При решении задачи рассмотрим худший случай
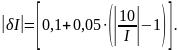
Для измеряемого диапазона находим
-
при
-
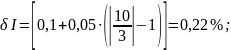
при
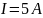
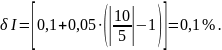
Средняя относительная погрешность
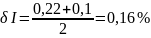
Второй
амперметр. Класс точности вольтметра
задан числом в кружке, следовательно,
относительная погрешность, выраженная
в процентах, во всех точках шкалы не
должна превышать по модулю класса
точности, т.е.
.
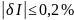При
рассмотрении худшего случая получаем
относительную погрешность
.
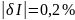Третий амперметр. Класс точности вольтметра задан числом без кружка, следовательно, приведенная погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. |γI| ≤ 0,2%.
Рассмотрим худший случай |γI| = 0,2%, когда приведенная погрешность принимает максимальное значение.
Рассчитаем абсолютную погрешность.
Из формулы
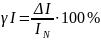
выражаем абсолютную погрешность
За нормирующее значение принимаем размах шкалы, так как шкала амперметра содержит нулевую отметку , т.е.
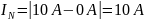
Абсолютная погрешность равна
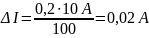
во всех точках шкалы прибора.
Значение относительной погрешности будем рассчитывать по формуле
- при I = 3А
- при I = 5А
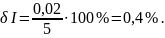
Средняя относительная погрешность
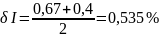
Первый и второй амперметры подходят для измерения с заданной точностью амперметр, из них наиболее точным является первый.