3 Способы и точность определения площадей земельных участков

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей:

• аналитический: площадь вычисляется по результатам измерений линий на местности, результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур);

• графический: площадь вычисляется по результатам измерении линий или координат на плане (карте);

• механический: площадь определяется по плану с помощью специального прибора (планиметра) (Приложение 1). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.

Площади можно также определить на ЭВМ по цифровой модели местности с помощью специальных программ.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) они разбиваются на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. В этом случае площади участков определяются как суммы площадей отдельных фигур, вычисляемых по линейным элементам — высотам и основаниям.

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по формулам, приведенным применительно к следующим фигурам участков:

- треугольник (рис.3.1, а). Площадь треугольника определяется по сторонам l₁ и l₂, углу ₂, заключенному между ними, по формуле

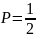
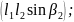(1)

- четырехугольник (рис. 3.1, б). В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризующий это многообразие. Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь треугольника 1—2—3 может быть вычислена по формуле (1).

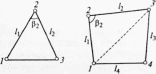
a б

Рис.3.1. Геометрические фигуры для определения площадей участков:

а – треугольник; б - четырехугольник

При этом полезно вычислить длину l_1-3, используя теорему косинусов:

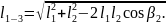
Площадь треугольника 1—3—4 может быть вычислена по формуле

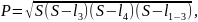
где – полупериметр.

Общая площадь четырехугольника

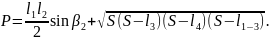
При наличии координат вершин полигона площади треугольника и четырехугольника удобно вычислять соответственно по следующим формулам:

Р = 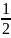[(X₁ - X₂)(Y₂ – Y₃) - (Y₁ - Y₂)(X₂ – X₃)];

Р = [(X₁ – X₃)(Y₂ – Y₄) - (Y₁ – Y₃)(X₂ – X₄)].

Если полигон имеет более четырех углов, то площадь его быстрее и с хорошим контролем можно получить по координатам X_i и Y_i его вершин или по приращениям координат ΔХ_i и ΔY_i после увязки полигона, например по следующим формулам:

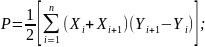
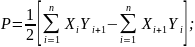
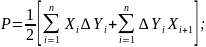
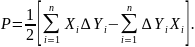
Координаты вершин полигона для определения площади участка как в государственной, так и в местной системах могут быть получены любым из геодезических способов: триангуляционными или линейно-угловыми построениями; проложением полигонометрических или теодолитных ходов; угловыми, линейными и полярными засечками; спутниковыми приемниками для определения местоположения.

Иногда возникает необходимость получения площадей физической (топографической) поверхности участка Р_ф, которая тем больше отличается от площади горизонтального проложения участка Р_г.п, чем больше угол наклона v или уклон i местности. Для получения площади физической поверхности участка его разбивают на части с одинаковыми скатами, т.е. с равностоящими, и более или менее прямыми горизонталями. На каждой из этих частей в перпендикулярном направлении к горизонталям определяют угол наклона или уклон и вычисляют площадь Р_ф на физической поверхности земли по следующим формулам:

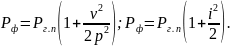
Например, уже при угле наклона v = 2,9° (уклоне i = 0,05) поправка составит 1:800 или 12,5 м² на 1 га.

Требования к точности определения площади земельных участков зависят от многих факторов: хозяйственной значимости (сельхозугодья, лесные угодья, городская территория и т.п.), местоположения (центр города, его окраина и т.п.), экологической обстановки (химическая загрязненность земли, атмосферы и т.п.), наличия и ценности недвижимости. Все эти и другие возможные факторы влияют на нормативную стоимость земли, которая в основном и является исходной для расчета требуемой точности определения площади земельных участков.

Достижение требуемой точности возможно лишь при правильном выборе способа определения площади участка. Очевидно, что наивысшая точность может быть достигнута при аналитическом способе определения площади. В этом способе площадь участка определяется по результатам измерений на местности, погрешность в определении площади будет зависеть от погрешностей этих измерений.

Например, для прямоугольника со сторонами а и b погрешность определяется площадью и вычисляется по формуле:

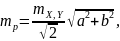(2)

где 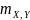– погрешность определенных координат

Так, например, если для участка размером 100 х 100 м (площадью 1 га) определять координаты со средней квадратической погрешностью 0,02м, то погрешность площади будет равна 2 м².

Для погрешности площади участка, определяемой по топографическому плану (карте), с учетом погрешностей измерений на местности и погрешностей составления топографического плана используется формула следующего вида:

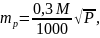(3)

где М — знаменатель численного масштаба плана; Р — площадь участка, м².

Таблица 3.1

Площадь Р, м2	Погрешность m, м2, масштабов
	1:500	1:1000	1:2000
400	3,0	6,0	12,0
600	3,7	7,3	14,6
1200	5,2	10,4	20,8
2500	7,5	15,0	30,0
10000	15,0	30,0	60,0

В табл. 3.1 приводятся величины средних квадратических погрешностей, вычисленных по формуле (3) для различных площадей участков по планам различных масштабов.

Приведенные формулы являются приближенными, так как не учитывают возможных погрешностей исходных данных и зависимости между входящими в них величинами. Однако они вполне достаточны для предварительных (проектных) расчетов.