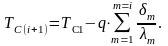1. Поле температуры. Градиент температуры.

Под потенциалом понимают любую величину, неоднородность которой в пространстве приводит к микроскопическому переносу соответствующей субстанции.

Под полем потенциала понимают совокупность значений потенциала во всех точках изучаемой области для любого момента времени. Если в качестве потенциала выбирают температуру, то соответственно речь идет о поле температур. Геометрическое место точек одинаковых потенциалов в потенциальном поле образует изопотенциальные поверхности. Например, в температурном поле ими являются изотермические поверхности. Различают нестационарные и стационарные поля потенциалов. Если поле зависит от времени, оно нестационарное. Например, нестационарные поля температур и скоростей течения жидкости в декартовой системе координат имеют вид.

Рассмотрим частный случай двумерного поля потенциала: двумерное температурное поле. На рис. 1.1 представлены три изотермические линии: T-T, T и T+T.

Выберем на изотермической линии Т точку А и проведем из нее нормаль к этой линии . Обозначим расстояние между изотермами Т и Т + Т через n. Градиентом температуры называется предел отношения

, (1.5)

где – единичный вектор нормали.

Спроектируем градиент температуры на координатные оси

,

,

Тогда градиент температуры можно записать в виде

. (1.6)

Соответственно модуль градиента температуры равен

(1.7)

Температура – скалярная величина, а градиент температуры – векторная величина. Градиент скорости (векторной величины) является тензором второго ранга, у которого, в отличие от вектора, девять компонентов в проекциях на координатные оси.

2. Стационарная теплопроводность однослойной плоской стенки (условия 1 рода).

Пусть имеем плоскую стенку толщиной  с постоянным коэффициентом теплопроводности . На наружных поверхностях стенки поддерживают постоянными температуры Т_С1 и Т_С2.

Рис. 3.1

В связи с этим температура будет зависеть только от одной координаты x, и дифференциальное уравнение теплопроводности (3.4) будет иметь вид

(3.7)

Граничные условия первого рода зададим следующим образом:

при x=0 T=T_C1,

при x= T=T_C2. (3.8)

Первое интегрирование (3.7) дает

(3.9)

После второго интегрирования получим

T=C₁x+C₂. (3.10)

(3.11)

Так как коэффициент теплопроводности  и градиент температуры постоянны, по закону Фурье равна

(3.12)

(3.13)

Количество тепла, перенесенное через плоскую стенку за время :

(3.14)

3. Стационарная теплопроводность через многослойную плоскую стенку.

Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n однородных слоев. Будем полагать, что между слоями отсутствуют контактные термические сопротивления, т.е. температура на обеих соприкасающихся поверхностях двух слоев одинакова. Контактные термические сопротивления необходимо учитывать при больших плотностях теплового потока q25000 вт/м² 2. При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, один и тот же.

В противном случае разность подведенного и отведенного потока тепла по закону сохранения энергии пошла бы на изменение энтальпии самой стенки и ее температура во времени не осталась бы постоянной. Так как у плоской стенки боковые поверхности одинаковы, то и плотность теплового потока при стационарном режиме во всех точках стенки q = const. При заданных температурах на внешних поверхностях такой стенки T_C1 и T_Cn+1, толщине слоев _i, где i = 1,2,….,n, и коэффициентах теплопроводности материалов этих слоев _i можно, используя (3.12), для каждого слоя записать

……………………..