1. Понятие модели. Принципы моделирования

Модель — объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала. Основная цель моделирования — исследовать эти объекты и предсказать результаты будущих наблюдений. Однако моделирование — это еще и метод познания окружающего мира, дающий возможность управлять им. 

Моделирование (процесс построения модели) – замещение одного объекта другим с целью изучения его свойств или поведения в тех или иных условиях. Виды моделирования: 

1. Вещественные:

а) Натуральные – реальные объекты, процессы и системы, над которыми выполняются научные, технические и производственные эксперименты.

б) Физические – макеты, муляжи, воспроизводящие физические свойства оригиналов

в) Математические – аналоговые, структурные, геометрические, графические и цифровые модели.

2.        Идеальные:

а) Наглядные – чертежи, карты, схемы, голограммы, графики, графы, аналоги, модели.

.       б) Знаковые – символы, алфавит, языки программирования, упорядоченные записи.

в) Математические – аналитические, функциональные, имитационные и комбинированные модели . Этапы моделирования:

1. Постановка задачи.

Определяется цель анализа, вырабатывается подход к исследованию проблемы.

2. Изучение теоретических основ и сбор информации об объекте оригинала.

Подбирается или разрабатывается подходящая теория, если ее нет, устанавливаются причинно-следственные связи между переменными, описанными объектами, определяются входящие и выходящие данные, принимаются упрощенные предложения.

3. Формализация.

Выбор системы условных обозначений, устанавливается класс задачи, к которой может быть отнесена полученная математическая модель.

4. Выбор метода решения.

Устанавливаются окончательные параметры модели для получения математической задачи, выбирается который либо метод решения или разрабатывается специальный.

5. Реализация модели.

Пишется программа, которая отлаживается, тестируется и получается решение задачи.

6. Анализ полученной информации.

Сопоставляются полученное решение и предполагаемое.

7. Проверка адекватности реальному объекту.

Результаты, полученные по модели, сопоставляются либо с имеющейся в объекте информацией, либо проводится эксперимент и его результаты сопоставляются с расчетными.

2. Классификация моделей.

1. По области использования:

         Учебные модели – используются при обучении;

         Опытные – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик

         Научно-технические -  создаются для исследования процессов и явлений

         Игровые – репетиция поведения объекта в различных условиях

         Имитационные – отражение реальности в той или иной степени (это метод проб и ошибок) 

 2. По фактору времени:

         Статические – модели, описывающие поведение объекта в определенный момент

         Динамические – модели, описывающие поведение объекта во времени

 Дискретные – параметры объектов могут принимать значения из фиксированного набора состояний.

 Непрерывные – параметры системы могут принимать значения из заданного диапазона

 3. По отрасли знаний - математические, биологические, химические, социальные, экономические, исторические и т. д. 

 4. По форме представления:

         Материальные – это предметные (физические) модели. Они всегда имеют реальное воплощение. Отражают внешнее свойство и внутреннее устройство исходных объектов, суть процессов и явлений объекта-оригинала. Это экспериментальный метод познания окружающей среды. Примеры: детские игрушки, скелет человека, чучело, макет солнечной системы, школьные пособия, физические и химические опыты

         Абстрактные (нематериальные) – не имеют реального воплощения. Их основу составляет информация, это теоретический метод познания окружающей среды. 

3. Математическая модель. Этапы математического моделирования. Классификация математических моделей

 Математическая модель – приближенное представление реальных объектов, процессов или систем, выраженных в математических терминах и сохраняющих черты оригинала.

Математическое моделирование – средство изучения реального объекта, процесса или системы, путем их замены математической моделью, более удобной для экспериментального исследования с помощью эвм.

Этапы моделирования:

1. Постановка экономической проблемы, главной задачей этого этапа является четкая формулировка сущности проблемы, применяемые допущения и те вопросы, на которые требуется получить ответы. Этот этап включает выделение черт, свойств модели объекта и абстрагирование от второстепенных, изучения структуры объекта, основных связывающих его элементов формирования гипотезы.

2. Построение математической модели. Этот этап формализации экономических проблем выражается в виде конкретных математических зависимостей ее отношений. Обычно сначала опираются от конструкции математической модели, а затем уточняются детали это конструкции.

3. Математический анализ модели – выяснение общих свойств модели.

4. Подготовка исходной информации

5. Численное решение задач включает разработку алгоритмов для численного решения задачи. Подбор необходимого ПО и проведение подсчетов

6. Анализ численного результатов и их применение

         Физическое – используется сама система, либо подобная ей (летательный аппарат в аэродинамической трубе).

         Математическое – процесс установления соответствия реальной системе S математической модели M и исследование этой модели, позволяющее получить характеристики реальной системы.

         Аналитическое – процессы функционирования элементов записываются в виде математических соотношений (алгебраических, интегральных, дифференциальных, логических и т.д.). Аналитическая модель может быть исследована методами:

а) аналитическим (устанавливаются явные зависимости, получаются, в основном, аналитические решения);

б) численным (получаются приближенные решения);

в) качественным (в явном виде можно найти некоторые свойства решения).

         Компьютерное – математическое моделирование формулируется в виде алгоритма (программы для ЭВМ), что позволяет проводить над ней вычислительные эксперименты.

         Численное – используются методы вычислительной математики (отличается от численного аналитического тем, что возможно задание различных параметров модели).

         Статистическое – обработка данных о системе (модели) с целью получения статистических характеристик системы.

         Имитационное – функционирование объектов, процессов или систем описывается набором алгоритмов, которые имитируют реальные элементы явления, составляющие процесс или систему, с сохранением их логической структуры и последовательности протекания во времени. Имитационное моделирование позволяет по исходным данным получить сведения о состоянии процесса или системы в определенный момент времени, однако прогнозирование затрудниельно.

4. Постановка задачи линейного программирования

1. Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на:

         наличие ресурсов

         величину спроса

         производственную мощность предприятия и другие производственные факторы.

 

Математическая модель любой задачи линейного программирования включает в себя:

         максимум или минимум целевой функции (критерий оптимальности)

         систему ограничений в форме линейных уравнений и неравенств

         требование неотрицательности переменных

5. Графическое решение задачи линейного программирования

Геометрическая интерпретация системы уравнений и целевой функции.

Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.

Каждое из неравенств задачи

 

 

линейного программирования определяет на координатной плоскости  некоторую полуплоскость,

а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи (1.2) ОДР является пустым множеством.

 

ЦФ  при фиксированном значении  определяет на плоскости прямую линию . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.

Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси  (начальная ордината), а угловой коэффициент прямой  останется постоянным (см.рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.

Вектор  с координатами из коэффициентов ЦФ при  и  перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора  совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора .

Суть графического метода заключается в следующем. По направлению (против направления) вектора  в ОДР производится поиск оптимальной точки  . Оптимальной считается точка, через которую проходит линия уровня , соответствующая наибольшему (наименьшему) значению функции . Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.

При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптимум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.

 

Методика решения задач ЛП графическим методом. (Походу это не входит в рамки вопроса, но на всякий пусть будет)

(Рис 1.)

 

 

1.        В ограничениях задачи (рис 1.) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые.

2.        Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи (рис 1.). Для этого нужно подставить в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверить истинность полученного неравенства.

                Если  неравенство истинное,

                то    надо заштриховать полуплоскость, содержащую данную точку;

                иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.

Поскольку  и  должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси   и правее оси , т.е. в I-м квадранте.

Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой. Поэтому необходимо выделить на графике такие прямые.

3.        Определить ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделить ее. При отсутствии ОДР задача не имеет решений.

4.        Если ОДР – не пустое множество, то нужно построить целевую прямую, т.е. любую из линий уровня    (где L – произвольное число, например, кратное  и , т.е. удобное для проведения расчетов). Способ построения аналогичен построению прямых ограничений.

5.        Построить вектор , который начинается в точке (0;0) и заканчивается в точке . Если целевая прямая и вектор  построены верно, то они будут перпендикулярны.

6.        При поиске максимума ЦФ необходимо передвигать целевую прямую в направлении вектора , при поиске минимума ЦФ – против направления вектора . Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).

7.        Определить координаты точки max (min) ЦФ  и вычислить значение ЦФ . Для вычисления координат оптимальной точки  необходимо решить систему уравнений прямых, на пересечении которых находится .

8.         

Вектор  C = (С₁, С₂) показывает направление наискорейшего возрастания целевой функции и называется вектором-градиентом целевой функции.

6. Целевая функция и ее оптимизация. Область решений системы неравенств

Целевая функция - это то, ради чего создается система. Если получаемые при заданных входных воздействиях значения целевой функции удовлетворяют заказчика, а стоимость такой системы минимальна, то такую систему считают эффективной, т.е. она является оптимальной.

Под эффективностью системы понимают ее способность выполнять заданные функции с наименьшими затратами ресурсов. Оптимизация системы должна проводиться именно по показателю эффективности, именно он определяет качество системы.

Выбор критерия эффективности - неформальная инженерная задача. Критерий должен выбираться исходя из целевой задачи системы, он должен иметь понятный физический смысл и измеряться в общепринятых физических единицах. В общем виде, в соответствии с вышесказанным, критерии оптимизации могут быть двух видов.

Имеется система с параметрами   входное воздействие стационарно и имеет вид   выбранная целевая функция имеет вид  Каждый параметр системы может изменяться и взвешивается стоимостью    z_i = f (d_i). В таком случае система будет оптимальной, если она отвечает критерию:

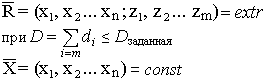
Либо в обратной постановке задачи:

7. Симплексный метод. Построение начального опорного плана

Назначение метода

В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом. 

Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).

Приведение к предпочтительному виду (3 случая). Построение начального опорного плана (X₀)

1.        Пусть в системе ограничений имеется единичный не отрицательный базис. X_i + a_ijx_j

= b_i;b_i>=0(i=1,m). Ограничения канонической задачи имеет предпочтительный вид если при не отрицательность его правой части (b_i>=0)левая часть содержит элементы с коэффициентом = 1, а остальные с коэффициентом = 0 , в это случае начальный опорный план строится следующим образом – предпочтительные переменные выбираются в качестве базисных , а все остальные свободны. Свободные переменные приравниваются к 0, базисные к свободным членам (b_i). 

2x₁ – 2x₃ +x₄ = 2   x4

2x₁ + x₂ - x₃ = 3  x3

X_j>=0;

X₀ = (0;3;0;2); Z(x₀)=0;

2.        Сведем задачу к каноническому виде, вводом дополнительной переменной x_n+i>=0 x₀=(0,…,0;b₁,…,b_m) дополнительные переменные входят в целевую функцию равную 0.

6x₁ + 15x₂ + 6x₃ + x₄<= 9;

14x₁ + 42x₂ + 16 x₃+ x₅<= 21 ;

2x₁+8x₂ + 2x₃ + x₆=4;

X₀ = (0,0,0,9,21,4)

Z_min= 10x₁ – 7x₂ – 5x₃

3.        Ea_ijx_j – x_n+I = b_iПроисходит  переход к м-задаче. Она имеет сл. вид max(min)Z = ∑c_jx_j –(+) M∑w_i; 

X_j>= 0 (1,n) w_i>= 0 (i = 1,m)

X1 + 21x2 + x3 + 2x4 <=3; +x5

-x1 -14x2 -2x3 + 3x4 >=2; -x6 +w1

-x1 – 6x2 + x3 - x4 >=1 ; - x7 + w2

 Min Z = -5x1 + 4x2 + 3x3 + 6x4 + 0*x5 + 0*x6 + 0*x7 + Mw1 + Mw2

X₀ = (0,0,0,0,3,0,0,2,1) Z(x₀) = 3M 

Пример: maxZ  = x1 + 2x2 + 3x3 + 4x4 + 5x5 -M w1 – 0*x6 - Mw2 – x7*0 – Mw3

X2 + x3 – 2x4 + 7x5 =2; +w1

X1 + x3 – 2x4 – 6x5 >= 12;  -x6 + w2

X1 + x2 - 2x4 + 7x5 >= 7;     -x7 +w3

X₀ = 0,0,0,0,0,0,0,2,12,7Z(x₀)= -21M

8. Симплексная таблица. Разрешающий элемент. Алгоритм решения

Симплексные таблицы

Приведя ЗЛП к предпочтительному виду, её заносят в симплексную таблицу.

 

max Z = 18x1 + 20x2 + 32x3

18x1 + 15x2 +12x3 + x4 = 720;

6x1 + 4x2 + 8x3 + x5 =384;

5x1 + 3x2 + 12x3 + x6 = 360;

Базисные переменные	Коэффициенты		A0		X1	X2		X3		X4		X5	X6
					18	20		32		0		0	0
X4	0		720		18	15		12		1		0	0
X5	0		384		6	4		8		0		1	0
X6	0		360		5	3		12		0		0	1
Zj - Cj		0		-18		-20	-32		0		0		0

 

∆₀ = 0*720 + 0* 384 + 0* 360 = 0;∆₀ = Z(x₀)

∆_I = ∑ коэфф. * a_ij  - c­_j;

∆₁ = 0*18 + 0*6+ 0*5 – 18= -18

 

Правило прямоугольника

Чтобы найти элемент новой симплексной таблицы, нужно воспользоваться правилом прямоугольника. Для этого в исходной таблице выделяют прямоугольник, вершинами которого служат нужные для вычисления элементы. Диагональ, содержащую разрешающий и искомый элементы новой таблицы, называют главной, а другую – побочной. Чтобы получить элемент новой симплексной таблицы, нужно из произведения угловых элементов главной диагонали вычесть произведение угловых элементов побочной диагонали и полученное число разделить на разрешающий элемент, выделенный рамкой.