1. Вращательное движение. Угловые величины.

2. Взаимосвязь между линейными и угловыми величинами.

3. Система кинематических уравнений, описывающих равнопеременное движение по окружности.

4. Система кинематических уравнений, описывающих движение тела, брошенного под углом к горизонту.

5. Примеры решения задач.

1 Вращательное движение. Угловые величины

Из истории науки. К XIV веку относятся сведения про ввод в научную терминологию понятия угловой скорости.

Т .к. при движении по окружности вектор скорости 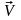постоянно меняет свое направление (рис.2.1), то говорить о равномерном движении по окружности некорректно.

Для описания движения по окружности полное ускорение раскладывается по правилу параллелограмма на составляющие, а его модуль рассчитывается по теореме Пифагора:

,

где 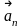– нормальное ускорение(центростремительное), – тангенциальное (касательное) ускорение.

Нормальное ускорениехарактеризует изменение скорости по направлению и равно отношению квадрату скорости к радиусу кривизны:

.

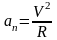Тангенциальное ускорениехарактеризует изменение скорости по величине и равно изменению скорости в единицу времени или равно первой производной линейной скорости по времени: .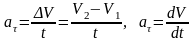

При вращательном движении вводятся угловые величины, аналогичные величинам, характеризующим поступательное движение: угол поворота, угловая скорость, угловое ускорение.

Угол поворота определяется как вектор по правилу правого винта (рис. 2.2). Скалярное значение угла поворота в Системе интернациональной измеряется в радианах: φ = [рад].

Угловая скорость характеризует угол поворота в единицу времени:

.

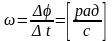Различают среднюю и мгновенную угловую скорость. Средняя угловая скорость численно равна отношению полного угла поворота ко времени, в течение которого это вращение произошло:

.

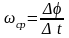Мгновенная угловая скоростьопределяется как предел отношения бесконечно малого угла поворота к бесконечно малому промежутку времени, в течение которого это вращение произошло, илиравна первой производной углаповоротапо времени:

.

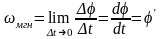Угловое ускорение численно равно изменению угловой скорости в единицу времени:

.

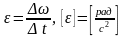Различают мгновенное и среднее угловое ускорение.

Среднее угловое ускорение равно отношению изменению угловой скорости ко времени, в течение которого это изменение угловой скорости произошло:

.

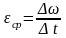Мгновенное угловое ускорение определяется как предел отношения бесконечно малого изменения угловой скорости к бесконечно малому промежутку времени, в течение которого это изменение угловой скорости произошло, т.е. равно первой производной угловой скорости по времени или второй производной угла поворота по времени:

.

2 Взаимосвязь между линейными и угловыми величинами

Взаимосвязь между углом поворота и длиной дуги окружности (рис. 2.2):

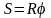, (3.1)

где S –длина дуги, R – радиус кривизны траектории, – угол поворота [] = [рад].

Дифференцируем уравнение (1) по времени dt: .

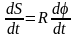После интегрирования получим взаимосвязь между линейной и угловой скоростями: 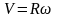. (3.2)

Продифференцируем уравнение (2) по времени dt: .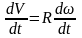

После интегрирования получим взаимосвязь между тангенциальным и угловым ускорением: 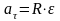. (3.3)