Типи задач для підсумкового контролю знань Типи задачі №1

Задача №1

На основі даних вибіркових статистичних спостережень для деякого регіону, які характеризують споживання продукту на душу населення ( y ) і ціну одиниці продукту ( x ) у грошових одиницях оцінити параметри економетричної моделі, що описує залежність споживання продукту на душу населення від його ціни і записати оцінене вибіркове рівняння регресії.

Номер спостереження	Споживання продукту на душу населення, грошові одиниці	Ціна одиниці продукту, грошові одиниці
1	55	10
2	57	7
3	56	5
4	59	6
5	51	12
6	58	8
7	60	6
8	61	5
9	65	4
10	68	3

Задача №2

На основі даних вибіркових статистичних спостережень для деякого регіону, які характеризують споживання продукту на душу населення ( y ), ціну одиниці продукту ( x₁ ) і доходи на душу населення ( x₂ ) у грошових одиницях оцінити параметри лінійної економетричної моделі, що описує залежність споживання продукту на душу населення від його ціни і доходів, та записати оцінене вибіркове рівняння регресії.

Номер спостереження	Споживання продукту на душу населення, грошові одиниці	Ціна одиниці продукту, грошові одиниці	Доходи на душу населення, грошові одиниці
1	55	10	216
2	57	7	220
3	56	5	222
4	59	6	230
5	51	12	212
6	58	8	235
7	60	6	240
8	61	5	241
9	65	4	242
10	68	3	245

Типи задачі №2 Задача №1

Дано:

; .

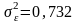Обчислити оцінки стандартних похибок 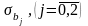параметрів економетричної моделі і перевірити статистичну значимість оцінок параметрів для рівня значимості =0,05. Об’єм вибірки становить n=15, а вибіркова модель має вигляд y = 12,35 + 0,45x₁ – 4,51x₂ + e.

Задача №2

Для вибіркової регресійної моделі дано :

i	1	2	3	4	5	6	7	8
yi	4,8	6,9	9,2	11,2	12,9	12,8	13,5	13,7
	5	7	9	11	13	13,5	13,7	13,9

За допомогою статистики Дарбіна – Уотсона перевірити модель на автокореляцію залишків для рівня значимості  = 0,05.

З

xi	5	6	9	12	18
yi	25	30	35	45	65

адача №3

Для статистичних даних побудована вибіркова

регресійна модель 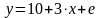. Обчислити стандартну похибку моделі і зробити відповідні висновки.

Задача №4

Для вибіркової парної лінійної регресійної моделі відомі наступні величини :

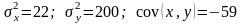, n=15. Обчислити коефіцієнт кореляції r_yx між x та y, коефіцієнт детермінації R², а також перевірити загальну статистичну значимість моделі для рівня значимості α = 0,05. Дати економічну інтерпретацію значень r_yx і R² ,якщо y – попит на деякі товари у грошових одиницях, а x – ціна одиниці товару.

Задача №5

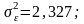
Дано : . Обчислити стандартні похибки оцінок параметрів економетричної моделі , якщо вибіркова модель має вигляд y = 0,987 + 0,897x₁ + 3,245x₂ + e., а об’єм вибірки становить n = 14.

Задача №6

Перевірити статистичну значимість і обчислити з рівнем довіри р = 0,95 довірчий інтервал для параметра β₁ в моделі , якщо об’єм вибірки n = 15, , b₁ = -0,59. Дати економічну інтерпретацію інтервалу довіри, якщо y – попит на деякі товари індивідуального споживання у грошових одиницях , а x – ціна одиниці товару у грошових одиницях.

Задача №7

За даними 8-ми річних спостережень побудована наступна модель інвестицій , де I_t – обсяг інвестицій у році t; r_t – відсоткова ставка у році t. У результаті тестування моделі доведено, що моделі притаманна автокореляція залишків. Побудувати матрицю S, якщо автокореляція залишків відповідає авторегресійній схемі AR(1) і дано :

t	1	2	3	4	5	6	7	8
It	4,8	6,9	9,2	11,2	12,9	12,8	13,5	13,7
	5	7	9	11	13	13,5	13,7	13,9