Движение жидкости (газа).

На основе общих законов механики движение жидкости (газа) описывается следующими соотношениями:

- уравнением сплошности, связывающим плотность движущейся среды плотностью  с её скоростью :

(3)

где J - объёмный источник изменения массы вследствие химических и фазовых превращений,  - время;

- уравнениями Навье-Стокса

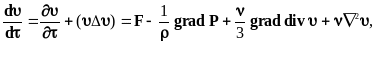( 4)

где  - кинематическая вязкость жидкости, F - внешняя объёмная сила, Р - давление жидкости.

Левая часть уравнения содержит сумму локального и конвективного ускорения, в правой части суммируются объёмная сила, давление и силы сопротивления, обусловленные вязкостью.

Приведенная выше система уравнений позволяет определить неизвестные функции скоростей  (x, y, z, ) и давления Р (x, y, z, ) при заданных значениях F (x, y, z, ), J (x, y, z, ), и . Решение подобной системы численными методами требует применения сложного математического аппарата и немалых затрат машинного времени. Для установившихся процессов, когда ускорениями в левой части уравнения (4) можно пренебречь, можно получить весьма известное уравнение Бернулли, используемое обычно для расчётов гидравлических режимов потоков.

Тепло- и массоперенос.

Дифференциальное уравнение переноса тепла в подвижной среде учитывает молекулярный перенос тепла кондукцией с коэффициентом теплопроводности  и конвекцией со скоростью  вследствие перемещения частиц жидкости:

(5)

где t - температура, с - удельная теплоёмкость, Q - внутренний объёмный источник тепла химических или фазовых превращений. Аналогичные соотношения используются и для описания процесса диффузии:

, (6)

где С - концентрация диффундирующего вещества, D - коэффициент диффузии, r - объёмный источник вещества. Уравнения дают значения С (x, y, z, ) и t (x, y, z, ), отвечающие конкретным условиям задачи, если указаны соответствующие граничные условия (законы распределения температуры (концентрации) в начальный момент времени и условия на границах рассматриваемого тела на протяжении всего процесса. Граничные условия конвективного теплообмена (переноса вещества) задают в форме уравнения Ньютона, для лучистого теплообмена - по закону Стефана-Больцмана.

Химические реакции.

Описание химических превращений складывается из стехиометрических соотношений, уравнения химического равновесия и описания кинетических закономерностей.

Стехиометрическое уравнение является кратким выражением материального баланса реакции:

(7)

где S_i - стехиометрические коэффициенты; для исходных веществ S_i<0, для продуктов реакции S_i>0; A_i - символы веществ, участвующих в реакции. Наиболее часто для решения стехиометрических задач используются методы линейной алгебры 1].

Расчёт химического равновесия позволяет выяснить принципиальную возможность получения тех или иных веществ в требуемых количествах, а также оценить содержание в них примесей и побочных веществ.

Существует несколько методик термодинамического анализа сложных систем. Простейшие основаны на решении систем уравнений, образованных выражениями для констант равновесия, совместно с уравнениями стехиометрического баланса. Для многокомпонентных гетерогенных систем (а это - большинство металлургических процессов), используются методы, основанные на принципе максимума энтропии (или минимума энергии Гиббса) для системы, находящейся в равновесии, и реализуемые только с помощью компьютерных технологий. [2,3,4].

Кинетика химической реакции описывается скоростью r изменения массы реагентов G в единице объёма V. Для гомогенных реакций или единицу поверхности S. Для гетерогенных процессов . Зависимость скорости реакции от концентрации реагирующих веществ записывается в виде

(8)

где n_i (i=1, 2, ..., m) - порядок реакции по веществу A_i; k - константа скорости химического процесса, выражаемая уравнением Аррениуса (k = k₀ exp (-E / RT) через энергию активации Е, R - универсальная газовая постоянная; k₀ - предэкспоненциальный множитель.