Определение бинарного дерева
Двоичным деревом поиска (ДДП) называют дерево, все вершины которого упорядочены, каждая вершина имеет не более двух потомков (назовём их левым и правым), и все вершины, кроме корня, имеют родителя [2]. Вершины, не имеющие потомков, называются листами. Подразумевается, что каждой вершине соответствует элемент или несколько элементов, имеющие некие ключевые значения, в дальнейшем именуемые просто ключами. Обычно одной вершине соответствует один элемент, поэтому данные термины можно без потери смысла считать синонимами, хотя и надо помнить, что в некоторых реализациях это не так. Под вставкой вершины понимается добавление вершины с указанным значением элемента и присвоение указателям на родителя и потомков корректных значений. Во всех операциях сравнения элементов используется, так называемый, ключ. Ключ – это уникальное поле, которое идентифицирует конкретнй элемент в бинарном дереве. Ключи используются не только в бинарных деревьях, но и в любой качественной базе данных. Элемент может также содержать ассоциированные с ключом данные. На практике в качестве ключа может использоваться часть данных элемента. Ключ также может храниться как отдельное значение. ДДП позволяет выполнять следующие основные операции:
поиск вершины по ключу;
определение вершин с минимальным и максимальным значением ключа;
– переход к предыдущей или последующей вершине, в порядке, определяемом ключами;
– вставка вершины;
– удаление вершины;
Двоичное дерево может быть логически разбито на уровни. Корень дерева является нулевым уровнем, потомки корня – первым уровнем, их потомки – вторым, и т.д. Глубина дерева – это его максимальный уровень. Понятие глубины также может быть описано в терминах пути, то есть глубина дерева есть длина самого длинного пути от корня до листа, если следовать от родительской вершины до потомка. Каждую вершину дерева можно рассматривать как корень поддерева, которое определяется данной вершиной и всеми потомками этой вершины, как прямыми, так и косвенными. Поэтому о дереве можно говорить, как о рекурсивной структуре. Эффективность поиска по дереву напрямую связана с его сбалансированностью, то есть с максимальной разницей между глубиной левого и правого поддерева среди всех вершин. Имеется два крайних случая – сбалансированное бинарное дерево (где каждый уровень имеет полный набор вершин) и вырожденное дерево, где на каждый уровень приходится по одной вершине. Вырожденное дерево эквивалентно связанному списку. Время выполнения всех основных операций пропорционально глубине дерева.
Таким образом, скоростные характеристики поиска в ДДП могут варьироваться от O(log2N) в случае законченного дерева до O(N) – в случае вырожденного.
Алгоритм бинарного поиска
Известно, что бинарный поиск эффективен, потому что он делит последовательности, в которых производится поиск, на две половины на каждой итерации. То есть большая часть информации даже не проверяется, так как в этом нет необходимости. Единственный недостаток – данные должны быть отсортированы [3].
Если представить следующую последовательность 0,1,2,3,4,5,6,7,8,9 в виде бинарного дерева, то получится дерево, показанное на рисунке 1.1.
Такова идея, скрытая за деревом. Такая структура называется деревом из-за ветвей, как у настоящего дерева. Возможно, эту структуру стоило бы назвать корнем бинарного поиска, т.к. это было бы проще увязать с иллюстрацией, походящей скорее на корневую систему, но, к сожалению, в информатике уже укоренилось название «дерево», так что переименование наверно было бы плохой мыслью.
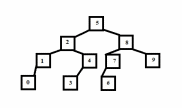
Рисунок 1.1 – Пример бинарного дерева из 10 элементов
Если начать поиск элемента с самого верхнего узла, называемого корнем, можно продолжать поиск заданного элемента, сравнивая его с вершиной на предмет того, меньше ли искомое значение, чем то, что содержится в вершине или же больше. Скажем, нужно найти элемент со значением 3. 3 меньше 5, поэтому двигаться нужно влево и текущей вершиной становится вершина со значением 2. 3 больше 2, поэтому идет смещение вправо и теперь вершиной становится узел 4, идет смещение влево от вершины и вот тот самый элемент 3. 3 равно 3, поиск удался. Следуя этому образцу, вы можете найти любой элемент в дереве.
В случае, если искомого элемента нет, необходимо проделать поиск, как описано выше и, если в результате алгоритм зайдет за нижнюю часть дерева, то поиск можно считать безуспешным. Для того, чтобы зафиксировать выход за нижнюю часть дерева в нем есть специальные узлы, называемые листьями (листовые узлы). Они не содержат данных и, если алгоритм достигает такого листа, значит поиск зашёл в тупик. Для обозначения листьев используются символы тильды ~, а дерево показано на рисунке 1.2.
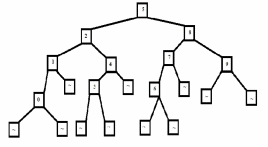
Рисунок 1.2 – Пример бинарного дерева
Из диаграммы легко увидеть, что при достижении листа поиск заканчивается. Вершина дерева называется корнем. Однако, учитывая то, что деревья могут определяться рекурсивно, каждый узел дерева может быть назван корнем (корень поддерева). Если узел является корнем поддерева, у него есть родительский узел, который ссылается на него. Так узел 2 является родительским узлом (родителем) узла 1, а 5 – родительский узел узла 2. Если смотреть с другой стороны, 2 является дочерним узлом узла 5, а 1 – дочерний узел (потомок) узла 2. В отношении деревьев принята аналогия с семейным древом.