1 ВОПРОС Измерение тока АЛС с помощью аппаратуры вагона лаборатории.

1 Система для измерения временных и электрических параметров числового кода. «КОНТРОЛЬ». Систему разработали во ВНИИЖТ. Измеряет ток 25, 50, 75Гц в диапазоне от 1 до 35А. с погрешностью +-10%, измерять временные параметры элементов числового кода с погрешностью 0,01сек при частоте несущей 50, 75Гц и +-0,2 при частоте несущей 25 Гц. Измерять временной интервал перерывов в кодировании от 2 до 9 секунд. Измерять координату места измерения в РЦ относительно изолирующего стыка с погрешностью 2%.

Функциональная схема системы «контроль»

Обозначения

ИК – измерительные катушки.

ДУ – дифференциальный усилитель, с помощью него подавляют симфазную помеху.

РФ – режекторный фильтр, ослабляет гармоники тягового тока.

СУ – селиктивный усилитель, настроенный на частоту несущей сигнального тока 25, 50, 75Гц.

НО – нуль орган – определяет переход сигнала через 0.

ФИФ – формирователь импульсов выборки.

АВД – автоматический выбор диапазона усиления. Кусилен =1, 2, 4, 8, 16.

СЗН1,3 – схема запоминания напряжения.

СЗН1 запоминает плюсовую амплитуду, а СЗН2 – минусовую.

БУ – балансный усилитель – устанавливает баланс между напряжениями.

ДФ – дифференциатор по фронту, ДС – дифференциатор по срезу.

ТВИ – триггер временного интервала.

Р – распределитель кодовых импульсов и интервалов.

ИВП – измеритель временных параметров кода.

ДИ – динамическая индикация. В В – выдержка времени.

ДОК – датчик оборотов колеса.

ФИ – формирователь импульсов.

ПЧ – преобразователь частоты 1 метр – 1 импульс.

ИС – измеритель скорости.

ГОЧ1 – кварцевый генератор.

ГОЧ2 – генератор с частотой 10 КГц для питания индуктора.

ДИС – датчик изолирующих стыков.

СУ2 – селективный усилитель, настроен на частоту 10 КГц.

Д – детектор.

АД – амплитудный детектор (триггер Шмидта).

СМ – счётчик пройденного пути.

ТИ – триггер изолирующего стыка.

2 Вопрос

4. ВОПРОС

Систематическая погрешность 1.4

Где - частные систематические погрешности определения величины у, вызванные систематическими погрешностями Sx,Sz,…Sw измеряемых величин x,z,…w.

Абсолютная придельная систематическая погрешность

1.5

Относительная предельная систематическая погрешность.

1.6

- это дифференциал от функции.

Случайные погрешности

Результат каждого отдельного измерения xi будет отличаться от истинного значения а. Разность между измеренным значением и истинным значением будет называться случайной погрешностью.

1.7 Xi – измеренное значение. а – истинное значение

Истинное значение «а» всегда неизвестно и предсказать результат каждого отдельного измерения невозможно, поэтому при измерениях используют статистические закономерности большого числа измерений и закон, по которому происходит распределение случайных погрешностей в зависимости от их величины.

Ряды случайных ошибок равноточных измерений обладают следующими свойствами:

1. по абсолютной величине случайные ошибки не могут превосходить определённого (известного) предела.

2. Малые по абсолютной величине ошибки встречаются чаще, чем большие.

3. Положительные ошибки появляются так же часто, как и одинаковые с ними по абсолютной величине отрицательные.

4. Сумма случайных погрешностей стремится к нулю. . Большие ошибке реже мелких, вот что это значит.

5 Вопрос Погрешности измерительных приборов (стрелочных)

Стрелочные измерительные приборы характеризуются номинальной относительной погрешностью.

1.8 - абсолютная погрешность измерения; В – показание прибора при измерении величины х.

Приведённая относительная погрешность 1.9

- максимальная абсолютная погрешность по шкале прибора;

Впр – максимальное (последнее) значение шкалы прибора.

По величине приведённой относительной погрешности приборы делят по точности на 8 классов: 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4 (ГОСТ-1845-69). В соответствии с этим гостом каждое число определяет в процентах приведённую относительную погрешность.

Обычно абсолютная величина погрешности прибора по всей шкале примерно одинакова, поэтому номинальная относительная погрешность измерения тем больше , чем меньше наблюдаемый по шкале отсчёт. Следовательно, прибор для измерения следует выбирать так, чтобы ожидаемое показание находилось в последней трети его шкалы. Погрешность измерительного приборка складывается из основной, которая возникает при нормальных условиях работы прибора из-за конструктивных недостатков, старения ламп, полупроводниковых приборов, и дополнительных, обычно систематических, которые возникают из-за работы прибора в условиях, отличных от нормальных.

7 Вопрос Обработка результатов измерений методами математической статистики

Методика построения эмпирической кривой

Если точность отсчётов по шкале и число измерений велико, то распределение ошибок можно изобразить графически в виде закона нормального распределения погрешности (Гауссовское распределение ошибок). Распределение называется нормальным, если плотность вероятности подчиняется нормальному закону: 2.1 У – плотность вероятности появления случайной ошибки Δх

Х – результат отдельного измерения А – истинное значение случайной величины

σ – среднеквадратическая погрешность измерений

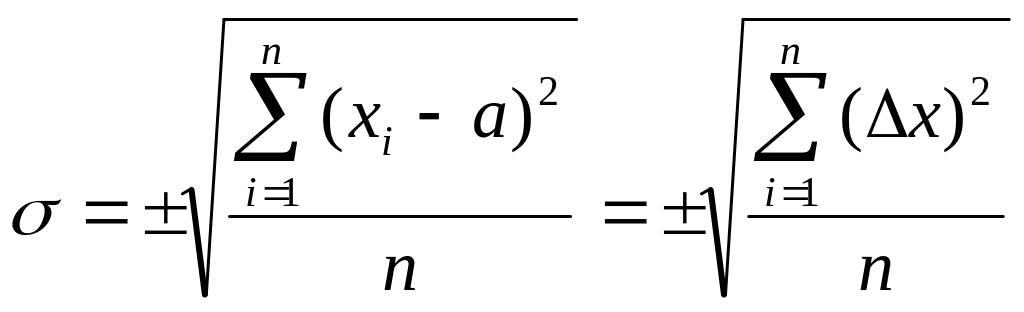
Так как истинное значение а всегда неизвестно, то вместо а берётся среднеарифметическое значение х из n измерений. Если число измерений равно или больше 25, можно использовать формулу:

Отклонение от среднеарифметического

Как известно из теории ошибок, среднее арифметическое х должно удовлетворять условиям:

1. Сумма 2.

При числе измерений не менее 25 среднеарифметическое определяется:

Кроме среднего значения и дисперсии (квадрат среднеквадратического отклонения), кривые распределения характеризуются асимметрией (А) и эксцессом (Е)

С увеличении м высоты кривой, характеризующей закон нормального распределения, увеличивается и точность измерений. А сама высота кривой h характеризует точность измерений и называется мерой точность. При небольшом числе измерений (10-12) средняя квадратическая ошибка полнее отражает влияние крупных ошибок, чем средняя ошибка.

Сравним 2 ряда измерений одной и той же величины:

1) +1, 0, -4, +3, -2, +3, -2, +3, -2, +3, -2, +2,

2)-7, +1, +8, 0, +2, -1, 0, -1, +1, -1

Из полученных результатов видно, что второй ряд измерений по точности хуже первого. В теории вероятности доказывается, что при n, стремящемся к бесконечности между средней и среднеквадратической ошибками существует связь: , между мерой точности h и средней ошибкой: , а между мерой точности и среднеквадратической ошибкой: .

Т очность и над1жность полученных значений среднего и среднеквадратического отклонения оценивается доверительной вероятностью и доверительным интервалом. Так как истинное значение Мх и σ неизвестны, найдём доверительный интервал +-Е, в который попадает истинное значение Мх, при заданной доверительной вероятности:

Поскольку измеряемая величина Хi распределена по нормальному закону, то и ошибка измерения δ распределена по нормальному закону , причём её среднее значение должно быть равно нулю.

Среднеквадратическое отклонение ошибки сигма дельта и исходного случайного процесса связаны соотношением: