Конспект лекций Стройникова ЕД, БГУИР (Мет пособие) / 09-10 лекция

§3.5. Симметрическая группа

Определение 3.5.1. Пусть  – конечное множество из n элементов для произвольного . Поскольку природа его элементов для нас не существенна, удобно считать, что  = {1, 2,…, n}. Всякая биекция, то есть взаимно однозначное преобразование  называется подстановкой на множестве . В развернутой и наглядной форме подстановку , i = 1, 2,…, n, удобно изображать в виде двухстрочной таблицы: . В этой таблице каждый i-й столбец четко указывает, в какой элемент f(i) преобразуется элемент i, .

Композиция подстановок, как композиция биекций, является подстановкой. Подстановки перемножаются в соответствии с общим правилом композиции функций: gf(i) = g(f(i)), i = 1, 2,…, n.

Пример 3.5.1. Пусть , . Тогда

,

аналогично . Как видим, fg  gf, то есть композиция подстановок не обладает свойством коммутативности.

Очевидно, тождественная подстановка играет роль нейтрального элемента относительно операции композиции подстановок. Как известно, композиция функций является ассоциативной операцией, поэтому и композиция подстановок ассоциативна. Каждая подстановка – обратимая функция. Чтобы найти для подстановки f обратную подстановку f ^–1, достаточно в таблице переставить строки местами, а затем столбцы упорядочить по возрастанию элементов первой строки.

Пример 3.5.2. Для подстановки найдем обратную подстановку f ^–1. Получаем, что . Чтобы убедиться в правильности вычислений, найдем композиции этих двух подстановок в том и другом порядке:

;

.

Таким образом, все подстановки на множестве  образуют в общем случае некоммутативную группу с операцией композиции подстановок.

Определение 3.5.2. Группу всех подстановок на n-элементном множестве относительно операции композиции называют симметрической группой степени n и обозначают S_n.

Несложно видеть, что все вышесказанное справедливо не только для конечного, но и для произвольного непустого множества . Таким образом, множество всех биективных преобразований  образует группу относительно операции композиции, обозначаемую S() и называемую симметрической группой множества .

Теорема 3.5.1. Порядок группы S_n равен n!.

Исходя из определения подстановки как взаимно однозначного преобразования n-элементного множества, утверждение справедливо согласно теореме 2.2.2.

Таким образом, | S₂ | = 2, | S₃ | = 6, | S₄ | = 24, | S₅ | = 120 и т.д.

Разложим подстановки из S_n в произведение более простых подстановок. Суть разложения сначала поясним, рассмотрев подстановки f и g из примера 3.5.1.

Пример 3.5.3. Подстановка f кратко записывается в виде f = (1 3 4 2) или, что то же самое, в виде f = (3 4 2 1) = (4 2 1 3) = (2 1 3 4) и носит название цикла длиной 4. Подстановка g = (1 3)(2 4) – произведение двух независимых (не пересекающихся) циклов (1 3) и (2 4) длиной два. Разложение в произведение независимых циклов подстановок f и g изображено на рис. 3.5.1.

Рис. 3.5.1

Перейдем теперь к общему случаю. Пусть S_n – произвольная симметрическая группа степени n и f – произвольная подстановка из S_n. Пусть Г_f = < f > – циклическая подгруппа в S_n, порожденная подстановкой f. Элементы i и j множества  = {1, 2,…, n} назовем Г_f -эквивалентными, если найдется такая подстановка для подходящего целого k, что g(i) = j. Тогда g^–1(j) = i. Очевидно, отношение Г_f -эквивалентности на множестве  рефлексивно (g = f ⁰ = e), симметрично (g(i) = j, g^–1(j) = i) и транзитивно . Тогда  разбивается на попарно непересекающиеся классы Г_f -эквивалентных друг другу элементов, называемых f-орбитами или Г_f -орбитами:  = ₁ … _p. Каждый элемент i   принадлежит в точности одной f-орбите, и если i  _k, то _k состоит из образов элемента i при действии степеней f: i, f(i), f ²(i),…, (i), где l_k = | _k | – длина f-орбиты _k. Очевидно, l_k  | < f > | – порядка подгруппы < f >. Ясно, что (i) = i, причем – наименьшее натуральное число с таким свойством.

Определение 3.5.3. Положим

.

Тем самым получим подстановку, называемую циклом длиной l_k, действующую тождественно на остальных элементах из .

Итак, f_k действует как f на _k и тождественно на \_k. Это дает основание считать циклы f_k и f_m при k  m независимыми или непересекающимися (так как они действуют на непересекающихся множествах _k и _m). Таким образом, разбиению  = ₁ … _p соответствует разложение подстановки f в произведение: , при этом циклы-сомножители независимы и перестановочны. Естественно в произведении опускать сомножители, соответствующие орбитам _i из одного элемента, так как – тождественная подстановка на .

Пример 3.5.4. Подстановку можно разложить в произведение независимых циклов следующим образом: f = (1 3 4 5 6)(2 8)(7) = (1 3 4 5 6)(2 8).

Итак, выше была доказана следующая теорема.

Теорема 3.5.2. Каждая подстановка , f  e, является произведением независимых циклов длинами l_k  2. Это разложение в произведение определено однозначно с точностью до порядка следования циклов.

Следствие. Порядок подстановки (порядок циклической группы Г_f) равен наименьшему общему кратному длин независимых циклов, входящих в разложение f.

Пусть – цикл длиной . Найдем в группе .

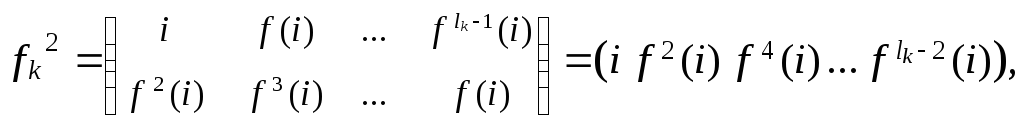
и т.д.,

Отсюда видно, что l_k – наименьшее натуральное число, такое что . Значит,  = l_k. Итак, порядок любого цикла равен длине этого цикла.

. Согласно теореме 3.5.2 каждая подстановка , f  e, является произведением независимых циклов длинами l_k  2, и это разложение определено однозначно с точностью до порядка следования циклов. Порядок подстановки делится на порядок каждого цикла, который входит в ее разложение, причем это наименьшее число с таким свойством по определению порядка элемента группы. Значит, порядок такой подстановки равен НОК порядков этих циклов, то есть длин этих циклов.

Определение 3.5.4. Цикл длиной 2 называется транспозицией.

Теорема 3.5.3. Каждая подстановка , f  e, разлагается в произведение транспозиций.

Согласно теореме 3.5.2 каждая подстановка , f  e, является произведением независимых циклов длинами l_k  2. Для доказательства данной теоремы достаточно убедиться в том, что каждый цикл длиной l_k  2 можно разложить в произведение транспозиций следующим образом:

.

Это проверяется непосредственным умножением транспозиций. Но данный способ разложения цикла длиной l_k  2 в произведение транспозиций не является единственным. Итак, каждая подстановка , f  e, разлагается в произведение транспозиций.

Пример 3.5.5. Разложим подстановку в произведение независимых циклов и транспозиций:

g = (1 4 6 8 3)(2 5 7 9) = (1 3)(1 8)(1 6)(1 4)(2 9)(2 7)(2 5) =

= (3 1 4 6 8)(5 7 9 2) = (3 8)(3 6)(3 4)(3 1)(5 2)(4 6)(5 9)(4 6)(5 7).

На данном примере убеждаемся в том, что разложение подстановки в произведение транспозиций неоднозначно.

Важно отметить, что любые два разложения одной и той же подстановки в произведение транспозиций содержат либо четное, либо нечетное число сомножителей.

Определение 3.5.5. Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, в противном случае она называется нечетной. Тождественную подстановку также относят к четным, полагая, что в ее разложении нуль транспозиций.

Таким образом, характер четности фиксированной подстановки не изменяется в зависимости от различных разложений в произведение транспозиций.

Теорема 3.5.4. Все четные подстановки группы S_n образуют подгруппу A_n; при n = 1 A_n = S_n, при n  2 | A_n | = n!/2.

Когда n = 1, A_n = S_n = {e}, поэтому, очевидно, A_n  S_n.

При n  2 покажем, что A_n  S_n согласно критерию подгруппы (теорема 3.3.1). Рассмотрим  f, g  A_n и разложим их в произведения транспозиций:

f = t₁…t_2k, g = ₁…_2l, где k, l  Z_0.

Тогда , поскольку в разложении количество всех транспозиций-сомножителей равно 2k + 2l = 2(k + l) – четное число. Итак, A_n  S_n.

Пусть n  2. Рассмотрим смежный класс A_n, где  – некоторая транспозиция. Получим класс нечетных подстановок: A_n  S_n\A_n. Допустим, | A_n | = | A_n | = a, а | S_n\A_n | = n! – a = b, тогда a  b. Теперь рассмотрим множество S_n\A_n всех нечетных подстановок и применим к ним одну и ту же транспозицию  – получим столько же четных подстановок, то есть | S_n\A_n | = | (S_n\A_n) | = b и (S_n\A_n)  A_n, поэтому b  a. Итак, a = b. Множества всех четных и нечетных подстановок не пересекаются и в объединении дают все множество S_n. Значит, | A_n | = | S_n\A_n | = n!/2.

Следствие. A_n – нормальная подгруппа группы S_n; при n  2 S_n : A_n = 2.

При n = 1 A_n = S_n = {e}, поэтому, очевидно, A_nS_n.

При n  2 согласно теоремам 3.5.4 и 3.4.2 S_n : A_n = | S_n |/| A_n | = n!/(n!/2) = 2. И, как было показано в примере 3.4.3, любая подгруппа индекса 2 нормальна. Следовательно, A_nS_n и в этом случае.

Определение 3.5.6. Подгруппа A_n всех четных подстановок группы S_n называется знакопеременной группой степени n.