Глава I. Основы теории чисел §1.1. Алгебраические операции на множестве целых чисел. Делимость целых чисел

Наиболее популярными числовыми множествами являются следующие:

N – множество натуральных чисел,

Z – множество целых чисел,

Q – множество рациональных чисел,

R – множество вещественных чисел,

C – множество комплексных чисел.

Они связаны следующим отношением включения: NZQRC.

Отношения >, <,  и  полностью упорядочивают множество R. Если A  R и a  A, то в дальнейшем будем обозначать A_>a, A_<a, A_a и A_a подмножества A, состоящие из всех чисел, больших a, меньших a, больших или равных a и меньших или равных a соответственно.

Множество целых чисел Z – счетное, состоит из элементов 0, 1, 2,…, n,… На нем определены две алгебраические операции – сложение и умножение. Эти операции обладают следующими общими свойствами (для любых a, b, c  Z):

1. ассоциативность: ,;

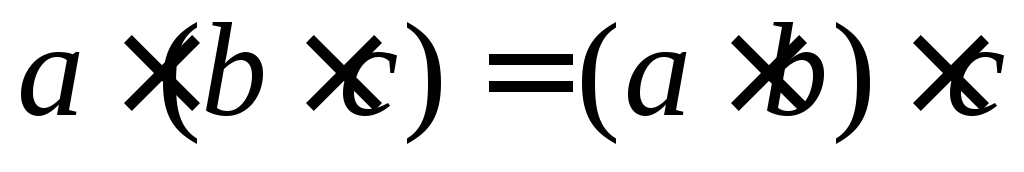2. коммутативность: ,;

3. существуют нейтральные элементы – 0 относительно сложения и 1 относительно умножения соответственно: , .

Кроме того, операция сложения обладает свойством:

4. для каждого существует единственноетакое, что:.

Ясно, что здесь – противоположное целое. Это свойство позволяет ввести наZ вспомогательную операцию – вычитание. – целое число – разность чиселa и , получаемое вычитаниемизa.

Умножение и сложение связаны свойством:

5. – закон дистрибутивности умножения относительно сложения.

Аналог свойства 4 для умножения выполняется лишь для двух целых чисел: 1 и –1.

Вообще говоря, для каждого целого существует обратное относительно умножения (то есть такое число, что), но оно является рациональным и не обязательно целым числом. Следовательно, результат операции деления целого числаa на целое число есть число рациональное и в редких случаях является целым. В общем же случае имеет место следующая теорема.

Теорема 1.1.1 (о делении с остатком). Для любых целых чисел a и , , существуют единственные целые числа и, 0  r < | b |, такие, что

. (1.1.1)

Доказательство существования.

1. . В этом случаеq = r = 0.

2. .

(вычитаем из a b столько раз, чтобы получилось число 0 или число r<b), .

3. .

, .

4. .

.

5. .

Доказательство единственности.

Пусть a = bq₁ + r₁ и a = bq₂ + r₂. Вычтем из 1-го равенства 2-е:

0 = bq₁ – bq₂ + r₁ – r₂,

b(q₂ – q₁) = r₁ – r₂.

Пусть q₁  q₂, тогда | r₁ – r₂ |  | b |, но 0  r₁, r₂ < | b |,  | r₁ – r₂ | < | b |. Значит, q₁ = q₂, поэтому и r₁ = r₂.

Определение 1.1.1. В равенстве (1.1.1) называютостатком, а –частным (неполным частным при ) от деления a на .

Для нахождения частного и остатка можно использовать метод деления «уголком».

Пример 1.1.1.

1

–

. .

.

2. .

203 = 16  12 + 11;

–203 = 16  (–12) – 11 = 16  (–12) – 16 + 5 = 16  (–13) + 5;

.

–

3. .

1

–

78 = 11  16 + 2;

–178 = (–11)  16 – 2 = (–11)  16 – 11 + 9 = (–11)  17 + 9;

.

4. .

7

–

25 = (–53)  (–13) + 36;

.

Определение 1.1.2. Если в равенстве (1.1.1) , то есть, то говорят, чтоa делится на (и пишут), чтоa является кратным числа , чтоделит a (и пишут b | a), а также называют делителем или множителем числа a. Все вышесказанное для b справедливо и для q при q  0. Будем обозначать , еслиа не делится на b, и ba, если не делитa.