MIHICTEPCTBO ОСВІТИ I НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ
«КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»
Факультет менеджменту та маркетингу
Практикум 6
з дисципліни
Економіко-математичні методи та моделі в економіці. Економетрика
На тему:
«Побудова економетричної моделі на основі системи одночастних структурних рівнянь»
Студентки ІІ курсу групи УС-31
Кугій Анна Андріївна
Перевірила:
Ільченко Ксенія Олександрівна
Лазаренко Ірина Сергіївна
Київ - 2015
Тема: Побудова економетричної моделі на основі системи одночастних структурних рівнянь.
Ціль роботи: Навчитись будувати економетричні моделі на основі системи одночасних структурних рівнянь, оцінювати статистичну значустісь характеристик зв’язку, визначити точковий та інтервальний прогнози ендогенних змінних.
Завдання до комп’ютерного практикуму:
Необхідно виконати наступні дії на основі вибраних вихідних даних:
1. Ідентифікувати змінні моделі.
2. Провести специфікацію моделі на основі одночасових структурних рівнянь.
3. Визначити індетифікованність кожного рівняння моделі.
4. Розрахувати оцінки параметрів моделі.
4.1. Перейти від структурної до приведенної форми рівнянь.
4.2. Розрахувати оцінки параметрів моделі методами 1МНК, НМНК, 2МНК, 3МНК.
4.3. Здійснити перехід від приведенної до структурної форми моделі.
5. Визначити асимптотичні стандартні помилки знайдених оцінок параметрів моделі.
6. Розрахувати прогнозні значення ендогенних змінних моделі на основі системи рівнянь.
7.Провести економічний аналіз одержанної інформації, сформувати висновки і пропозиції.
У ході роботи буде простежено зв’язок між показниками площі України, продукції зернових, ВВП з залученням прямих іноземних інвестиції (у), взяті за 1999 – 2013 роки. Оскільки Україна відзначилась на зовнішніх ринках в більшій частці як експортер сільськогосподарської продукції (більша частина якої припадає на зернові культури) у ході роботи висувається за метою визначення зв’язку між цією характеристикою та інвестиційною привабливістю України з точки зору аграрного виробництва.
Визначимось з теоретичними положеннями за даною темою.
Система одночасних рівнянь - сукупність економетричних рівнянь (часто лінійних), що визначають взаємозалежність економічних змінних. Важливою відмітною ознакою системи "одночасних" рівнянь від інших систем рівнянь полягає в наявності одних і тих же змінних в правих і лівих частинах різних рівнянь.
Ендогенними називаються змінні, значення яких визначаються в процесі функціонування досліджуваної економічної системи. Їх значення визначаються "одночасно" виходячи з значень деяких екзогенних змінних, значення яких визначаються поза моделлю, задаються ззовні. У системах одночасних рівнянь ендогенні змінні залежать як від екзогенних змінних, так і від ендогенних.
Вимірювання тісноти зв'язку між змінними, побудова ізольованих рівнянь регресії недостатньо для пояснення функціонування складних економічних систем. Зміна однієї змінної не може відбуватися при абсолютній незмінності інших. Її зміна потягне за собою зміни у всій системі взаємозалежних ознак. Таким чином окремо взяте рівняння регресії не може характеризувати істинне вплив окремих ознак на варіацію результуючої змінної. Тому в економічних дослідженнях важливе місце зайняла проблема опису структури зв'язків між системою змінних.
Наявність прямих та зворотніх зв’язків між економічними показниками в багатьох випадках вимагає використання системи одночасових рівнянь. Вони, як правило, містять лінійні рівняння. Нелінійність зв’язків апроксимується лінійними співвідношеннями. Динаміка економічних зв’язків ураховується за допомогою часових лагів або лагових змінних.
Система одночасових структурних рівнянь в матричному вигляді має такий вигляд:
.
Якщо
кожне рівняння системи розв’язати
відносно
,
то одержимо приведену форму моделі, яка
має вигляд:
,
де
залишки
є лінійною комбінацією залишків
.
Зв’язок між коефіцієнтами структурної і приведеної форми моделі визначиться:
,
або
,
або
.
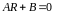Оцінка параметрів моделі на основі одночасових рівнянь методом 1МНК буде давати зміщення, яке буде дорівнювати:
,
де
— момент
другого порядку залежної змінної, який
прямує до деякої константи.
Чисельна оцінка параметрів моделі на основі одночасових структурних рівнянь пов’язана з проблемою ідентифікації.
Необхідна умова ідентифікації системи — справедливість нерівності для кожного рівняння:
де
— кількість ендогенних змінних, які
входять в
-те
рівняння структурної форми;
— загальна
кількість екзогенних змінних моделі;
— кількість
екзогенних змінних, які не входять в
-те
рівняння структурної форми моделі.
Якщо записане вище співвідношення виконується як рівність, то відповідне рівняння є строгоідентифікованим, а коли — як нерівність, то відповідне рівняння є надідентифікованим.
Якщо
в структурній формі моделі
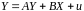матриця
є трикутною, а залишки характеризуються
діагональною матрицею виду:
,
то така система рівнянь називається рекурсивною і для оцінки параметрів такої моделі можна застосувати 1МНК.
Якщо кожне рівняння моделі є строгоідентифікованим, то для оцінки параметрів моделі можна застосувати непрямий метод найменших квадратів (НМНК). Алгоритм цього методу складається з чотирьох кроків:
Крок 1. Перевіряється умова ідентифікованості для кожного рівняння. Якщо кожне рівняння точноідентифіковане, то виконується перехід до кроку 2.
Крок 2. Перехід від структурної форми моделі до приведеної.
Крок 3. Оцінка параметрів кожного рівняння приведеної форми моделі 1МНК.
Крок 4. Розрахунок оцінок параметрів рівнянь структурної форми на основі співвідношення:
,
де
і
— параметри структурних рівнянь, а
— матриця оцінок параметрів приведеної
форми моделі.
Якщо рівняння структурної форми моделі надідентифіковані, то для оцінки параметрів моделі застосовується двокроковий метод найменших квадратів (2МНК). Система рівнянь для обчислення оцінок двокроковим методом найменших квадратів запишеться так:
,
де — вектор залежної або ендогенної змінної;
— матриця
поточних ендогенних змінних, які входять
у
праву частину рівняння;
Х — матриця всіх пояснюючих або екзогенних змінних;
— матриця
пояснюючих або
екзогенних змінних даного рівняння;
— вектор
структурних параметрів, які відносяться
до змінних матриці
;
— вектор
структурних параметрів, які відносяться
до змінних матриці
.
Oператор оцінювання 2МНК:
Дисперсія залишків для кожного рівняння:
.
Матриця коваріацій параметрів кожного рівняння визначається на основі співвідношення:
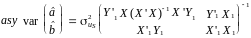
Трикроковий метод найменших квадратів (3МНК), на відміну від попередніх, призначений для одночасної оцінки параметрів всіх рівнянь моделі. Оператор оцінювання 3МНК матиме вигляд:
де
— оцінки параметрів моделі;
,
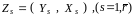де
—
змінні моделі, які знаходяться у правій
частині
-го
рівняння;
— дисперсії
залишків для кожного рівняння, які є
наближеною оцінкою
.
Щоб застосувати 3МНК на практиці, необхідно дотримання таких вимог:
1) приступаючи до оцінки параметрів моделі, необхідно виключити всі тотожності;
2) виключити із системи кожне неідентифіковане рівняння;
3) при наявності серед рівнянь системи точноідентифікованих та надідентифікованих, 3МНК доцільно застосувати до кожної з груп рівнянь окремо;
4) якщо група надідентифікованих рівнянь має тільки одне рівняння, то 3МНК перетворюється в 2МНК.
Якщо матриця коваріацій для структурних залишків є блочно-діагональною, то вся процедура оцінювання на основі 3МНК може бути застосована окремо для кожної групи рівнянь, які відповідають одному блоку.
Метод максимальної правдоподібності з повною інформацією (FIML) - метод, що використовує всю інформацію про обмеження на наведену форму моделі.
Метод максимальної правдоподібності з обмеженою інформацією (LIML, метод найменшого дисперсійного відносини) призначений для оцінки одного рівняння системи. Інші рівняння оцінюються лише в тій мірі, в якій це необхідно для оцінки даного рівняння. Перше оцінюється в структурній формі, решта в необмеженій наведеної, тобто використовується не вся доступна інформація при оцінці. Даний метод зводиться до знаходження мінімального власного числа певної симетричної матриці
Точковий прогноз залежних змінних визначається на основі приведеної форми економетричної моделі:
,
де
— вектор прогнозних екзогенних змінних.
Визначення
довірчих інтервалів для цього прогнозу
залежить від методу, за допомогою якого
була одержана матриця
Довірчі інтервали для кожної ендогенної змінної задаються сіввідношенням:
,
де
— дисперсія залишків
-
го рівняння моделі;
.
Довірчі інтервали для всіх ендогенних змінних визначаються так:
,
де
— незміщена дисперсія залишків всіх
рівнянь моделі.
Ці інтервали будуть ширшими, ніж у випадку, коли їх задавати для кожної ендогенної змінної окремо [1, C. 449]
Виконаємо практичні дії
Ідентифікувати змінні моделі.
Виходячи із обраних даних визначаємо, що
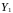— обсяг
залучення прямих іноземних інвестицій,
ендогенна змінна;
— обсяг
продукції зернових, вирощених на
території України,
ендогенна змінна;
–– територіальна
забезпеченість країни,
екзогенна змінна;
–– валовий
внутрішній продукт,
екзогенна змінна.
2. Провести специфікацію моделі на основі одночасових структурних рівнянь.
Система одночасних структурних рівнянь може бути подана у вигляді матричному:
Y=AY+BX+U
Y - матриця-вектор залежних змінних
X - матриця-вектор незалежних змінних
U - матриця-вектор залишків
A - матриця-вектор коефіцієнтів при Y, розмірності (k×k)
B – матриця-вектор коефіцієнтів при X, розмірності (k×m)
Або на основі структурних рівнянь:
;
;
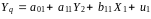Цю систему одночасових структурних рівнянь можна переписати у вигляді:
;
.
3. Визначити індетифікованність кожного рівняння моделі.
Для першого рівняння
;
;
;
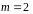Маємо
Де 2-1=2-1, 1=1, отже перше рівняння системи є точноідентифікованим.
Для другого рівняння
;
;
;
Маємо
Де 2-1=2-1, 1=1. Друге рівняння системи є також точноідентифікованим.
Оскільки обидва рівняння системи є точноідентифікованими, то оцінку параметрів моделі можна виконати непрямим методом найменших квадратів.
4. Розрахувати оцінки параметрів моделі.
У1 |
Уn |
(У1-Уn) |
(У1-Уn)^2 |
-1,30767 |
-0,14069 |
-1,166984085 |
1,361852 |
-1,33636 |
-0,07743 |
-1,258926793 |
1,584897 |
-1,12453 |
-0,3048 |
-0,819724965 |
0,671949 |
-1,0402 |
-0,0402 |
-1,000002476 |
1,000005 |
0,725433 |
-0,38344 |
1,108871505 |
1,229596 |
0,086756 |
-0,28148 |
0,368231328 |
0,135594 |
1,416561 |
-0,11555 |
1,532106379 |
2,34735 |
1,56348 |
0,253883 |
1,30959689 |
1,715044 |
-0,15521 |
0,162922 |
-0,3181333 |
0,101209 |
0,3322 |
0,079484 |
0,252716396 |
0,063866 |
0,551275 |
0,297491 |
0,253784104 |
0,064406 |
0,732678 |
0,167061 |
0,565616646 |
0,319922 |
-0,44441 |
0,382739 |
-0,827151629 |
0,68418 |
|
|
0 |
11,27987 |
Визначемо для другого рівняння з системи одночасних структурних рівнянь
У2 |
Уn |
(У2-Уn) |
(У2-Уn)^2 |
-0,22572 |
-0,76925 |
0,543534708 |
0,29543 |
-0,30253 |
-0,65661 |
0,35408078 |
0,125373 |
-1,89565 |
-0,63143 |
-1,264216048 |
1,598242 |
-0,04166 |
-0,37114 |
0,32948584 |
0,108561 |
-0,36656 |
-1,08284 |
0,716279508 |
0,513056 |
-0,69217 |
-0,20201 |
-0,490156568 |
0,240253 |
-1,0896 |
-0,33503 |
-0,7545705 |
0,569377 |
0,978847 |
0,351045 |
0,627802411 |
0,394136 |
0,341518 |
0,158933 |
0,182585172 |
0,033337 |
-0,24311 |
0,248024 |
-0,491129252 |
0,241208 |
1,284394 |
0,718758 |
0,565636535 |
0,319945 |
0,370517 |
0,835194 |
-0,464676741 |
0,215924 |
1,881702 |
1,736357 |
0,145344156 |
0,021125 |
|
|
7,21645E-16 |
4,675968 |
Оцінка параметрів.
Для першого рівняння системи Y1t=A11*Y2t+ B10*Xot+B11*X1t+U1t отримаємо
А21 |
-0,135340957 |
В10 |
-6,65926E-14 |
В11 |
0,137122175 |
Відповідно для другого рівняння системи Y2t=A21*Y1t+ B20*Xot+B22*X2t+U2t
А11 |
-0,661800314 |
В10 |
-1,66533E-16 |
В11 |
1,152833353 |
4.1. Перейдемо від структурної до приведеної форми рівнянь. Для цього в другому рівнянні замість підставимо вираз у правій частині першого рівняння.
Запишемо:
(1);
(2).
Підставимо
значення
у друге рівняння, звідси:
;
;
;
.
Розділимо
обидві частини рівняння на
і отримаємо:
.
Замінимо
;
;
.
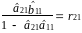В результаті отримаємо друге рівняння моделі в приведеній формі:
.
А
тепер значення структурного рівняння
(2) підставимо в перше рівняння моделі
(1) і приведемо його до приведеної форми.
;
.
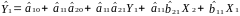Перенесемо
в ліву частину рівняння:
.
Розділимо
обидві частини рівняння на
і отримаємо:
.
Замінимо:
;
;
.
В результаті отримаємо перше рівняння моделі в приведеній формі:
.
Таким чином, економетрична модель в приведеній формі:
;
.