5.3.2. Способы представления рельефа нелинейными методами Полиномиальные методы

Полиномиальные способы предполагают представление модели­руемой поверхности полиномом второй - пятой степени вида

(5.8)

Для отыскания неизвестных коэффициентов полинома для каждой опорной точки составляют одно уравнение поправок вида

(5.9)

где свободный член (Z – Z_Г) представляет собой уклонение вычислен­ной по формуле (5.7) отметки (Z) с приближенными значениям ко­эффициентов полинома от исходной (Z_Г). Полученную систему реша­ют последовательными приближениями, в каждом из которых неизве­стные находят методом наименьших квадратов, под условием [pv ]= min. Найденные таким образом коэффициенты а₀...а_i уравнений (5.7) используют для интерполяции высот точек, расположенных в области моделирования.

Кусочно-полиномиальные способы предполагают деление области моделирования на участки, подбор для каждого участка своего ло­кального полинома вида (5.7) и последующую связь локальных поли­номов с помощью переходных уравнений. Во всех случаях возникают переопределенные системы, которые решаются под условием миниму­ма суммы квадратов расхождений высот точек реальной и аппроксими­рующей поверхностей.

Сходные по характеру решения используют способы, основанные на применении рядов Фурье (разложений по сферическим гармони­кам), различного рода сплайнов (кубических, бикубических, на много­образиях и др.) и т. п. [3].

На русский язык термин "spline" переводится как "гибкая рейка" или "плавная кривая" [5].

Сплайны используются для сглаживания линий при отображении гладких поверхностей (поле и т.д.).

Мультиквадриковый способ аппроксимации топографической поверхности

В этом способе аппроксимация топографической поверхности осуществляется путем суммирования поверхностей заранее фиксированного вида, в качестве которых применяются конусы и гиперболоиды. Каждая такая поверхность, характеризуемая уравнением

связана с некоторой точкой топографической поверхности j и имеет определенный наклон c_j . Элемент называется кадрикой точки j.

Для n квадрик аппроксимирующая топографическую поверх­ность формула получается как сумма частных квадрик

и называется мультиквадриковой поверхностью.

Квадрика q, представляемая гиперболоидом, имеет вид

(5.8)

При В=0 гиперболоид превращается в круговой конус, радиус основания которого равен высоте, а вершина лежит в плоскости XOY. Координаты вершины совпадают с координата­ми и точки j.

Коэффициенты получаются из решения системы n урав­нений

i=1, 2, …, n (5.9)

где -я компонента вектора z=[ ] -я компонента вектора неизвестных коэффициентов ; q(x_j, y_j, x_i, y_i)— эле­менты q_i матрицы

Q = [q_ij ],

В матричной форме система уравнений (1) примет вид

Qc=z

откуда

С геометрической точки зрения коэффициенты с_j — танген­сы углов наклона образующих соответствующих конусов к плоскости XOY.

Координата z_A любой определяемой точки на вычисленной мультиквадриковой поверхности получается как сумма всех z_j^A точек пересечения каждой частной квадрики с вертикаль­ной линией, проходящей через точку A,

Величина параметра В в формуле (5.8) может принимать различные значения в зависимости от сложности рельефа и размеров стороны квадрата.

Как показали исследовании, мультиквадриковая поверхность наиболее адекватна топографической поверхности, когда значение параметра В имеет тот же порядок, что и квадрат стороны участка аппроксимации. При неправильном выборе этого параметра происходит систематический сдвиг поля высот.

Методы нелинейной интерполяции

Слово крикинг (Kriging) является синонимом «оптимального прогнозирования». Это метод интерполяции, который определяет неизвестные значения по данным наблюдений с известным положением. Этот метод использует вариограммы, чтобы предать пространственные изменения, и минимизирует ошибки определяемых значений, которые оцениваются пространственным распределением оцениваемых значений. Kriging был разработан Матероном (Matheron) и Кригом (Krige).

Метод интерполяции кригинг (kriging), оптимизирует процедуру интерполяции на основе статистической природы поверхности полиномами первого, второго и третьего порядка (рис.5.10).

Рис.5.10. Порядки поверхностей тренда. Поверхности первого, второго и третьего порядка в зависимости от сложности полинома, используемого для представления поверхности.

Кригинг использует идею регионализированной переменной, которая изменяется от места к месту с некоторой видимой непрерывностью, но не может моделироваться только одним математическим уравнением. Оказывается, многие топографические поверхности подходят под это описание [12].

Кригинг обрабатывает эти поверхности так, считая их образованными из трёх независимых величин. Первая, называемая дрейфом или структурой поверхности, представляет поверхность как общий тренд в определённом направлении. Далее, крикинг предполагает, что имеются небольшие отклонения от этой общей тенденции, вроде маленьких пиков и впадин, которые являются случайными, но всё же связанными друг с другом пространственно (пространственно коррелированные). Наконец, мы имеем случайный шум, который не связан с общей тенденцией и не имеет пространственной автокорреляции. Если двигаться вверх по склону, рельеф местности изменяется в восходящем направлении между отправной точкой и вершиной; это – дрейф. По пути мы встречаем локальные снижения и повышения, сопровождаемые случайными, но коррелированными высотами. Также по пути нам встречаются локальные неровности, которые можно представлять как шум значения высоты, так как они не связаны непосредственно с основной поверхностной структурой, прежде всего создающей изменения высоты (Рис.5.11.)

С каждой из трех переменных надо оперировать в отдельности. Дрейф оценивается с использованием математического уравнения, которое наиболее близко представляет общее изменение поверхности, во многом подобно поверхности тренда. Ожидаемое значение высоты измеряется с использованием вариограммы (рис.5.12), на которой по горизонтальной оси откладывается расстояние между отсчетами, называемое лагом, вертикальная ось несет так называемую полудисперсию, которая определяется как половина дисперсии (квадрата стандартного отклонения) между каждым значением высоты и его соседями.

Таким образом, полудисперсия является мерой взаимосвязи значений высоты, зависящей от того, как близко друг к другу они находятся. Затем через точки данных проводится кривая наилучшего приближения, давая меру пространственно-коррелированной случайной компоненты [12].

Рис.5.11. Элементы кригинга. Дрейф (общая тенденция), случайные, но пространственно коррелированные высотные колебания (небольшие отклонения от общей тенденции), и случайный шум.

Из графика видно, когда расстояние между точками отсчета высоты близки и, следовательно, взаимосвязаны вследствие их пространственной близости. С ростом расстояния между точками растет и полудисперсия, показывая быстрый спад пространственной корреляции значений.

Рис.5.12.Пример вариограммы. Она показывает связь между точками данных и аппроксимирующей линией.

Метод крикинга можно представить путем регионализации переменных с учетом весовых коэффициентов, которые распределены по определенному закону (вариограммы) , в зависимости от расстояния между реальной точкой и искомым узлом сетки (грида) [7]:

(5.10)

Чаще всего метод крикинга использует две модели вариограмм:

1. сферическая

2. экспотенциальная

В некоторых случаях могут применятся следующие вариограммы [6]:

Гаусса:

Квадратичная:

Квадратичная относительная:

Степенная

Волновая (Эффект Холла)

Логарифмическая

Где:

- масштабный коэффицент, - анизотропия, относительно выбранного расстояния.

Еще одним способом восстановления непрерывной поверхности явля­ется ее представление в виде среднего весового (Inverse Distance):

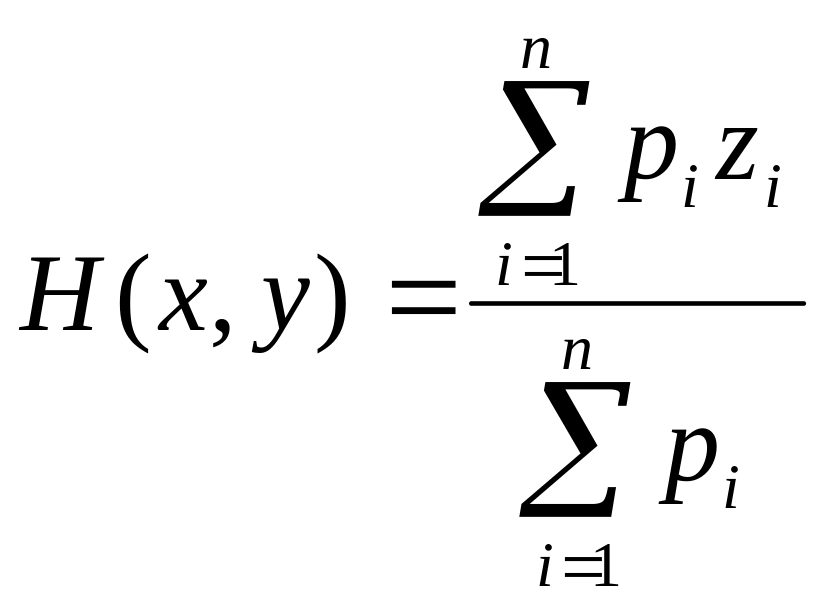(5.11)

где вес р - некоторая положительная убывающая функция от расстояния [9]. Конкретные реализации данного метода отличаются, в основ­ном, способом определения весовых функций. Привлекательная сторона метода среднего весового состоит в том, что при его использовании не требуется решать системы уравнений, и значение высоты поверхности может быть получено в любой ее точке непосредственным применением формулы (5.11). Особенность данного метода состоит также в том, что в зависимости от определения весовой функции он является либо интер­поляцией, либо аппроксимацией.

Этот метод является наиболее простым методом как в теоретическом плане, так и в плане практической реализации на PC. Чаще всего значение в узле представляется суммой произведений значения в точке измерения и некоторого весового коэффициента, который зависит от множества различных параметров, но, прежде всего, – от расстояния до узла. Значение в узле может быть вычислено [6] по значениям в соседних точках , расположенных на расстоянии от узла:

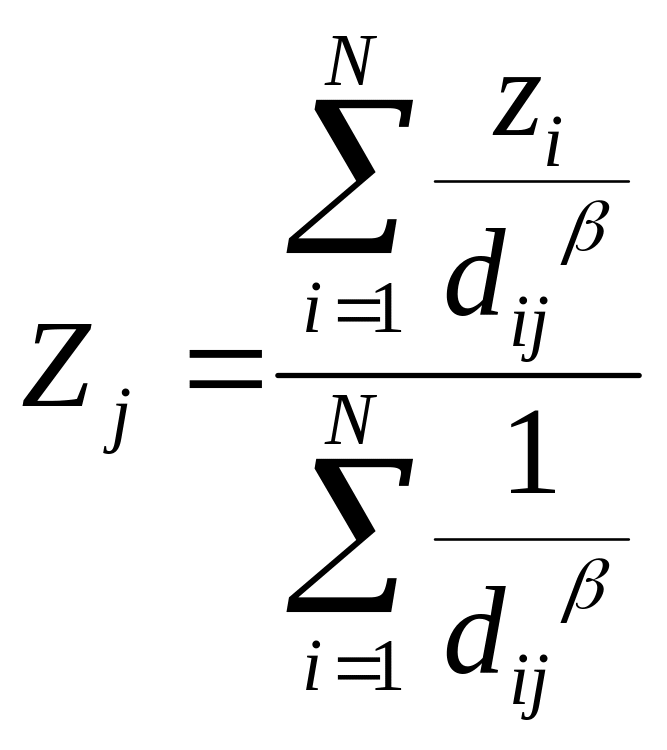(5.12)

Параметр выбирается исходя из конкретных условий и может принимать значения от 1 до 10.

Задачи, решаемые с использованием цифровых математических моделей

В рамках системного автоматизированного проектирования (САПР) объектов строительства с помощью цифровых и математических моделей решается широкий круг инженерных задач, которые ранее частично находили решение другими методами и средствами:

• оптимальное пространственное трассирование автомобильных дорог, лесовозных дорог и каналов. Решение этой актуальной задачи с привлечением математического аппарата оптимизации проектных решений стало возможным благодаря развитию методов цифрового и математического моделирования местности;

• получение продольных профилей Земли по оси вариантов трассы, запроектированных с использованием крупномасштабных топографических планов. В рамках изысканий при традиционном проектировании продольный профиль по оси трассы получали в результате выполнения трудоемкого комплекса полевых геодезических работ, как правило, средствами традиционной наземной геодезии (трассирование, закрепление трассы, разбивка пикетажа, двойное геометрическое нивелирование и т.д.);

• получение поперечных профилей Земли. Эта работа при традиционных изысканиях выполнялась, как правило, методом тригонометрического нивелирования;

• получение продольных по оси трассы и поперечных инженерно-геологических разрезов. При традиционных изысканиях эту совершенно необходимую для проектирования информацию получали в результате выполнения комплекса чрезвычайно трудоемких и дорогих инженерно-геологических работ путем механического бурения, шурфования, устройства расчисток и т. д.;

• получение исходной инженерно-гидрологической информации для проектирования водопропускных сооружений и системы поверхностного водоотвода (площади водосборов, живые сечения, морфостворы и гидростворы, уклоны логов и их склонов, математическое моделирование стока ливневых и талых вод и т.д.);

• проектирование системы дорожного поверхностного водоотвода (кюветы, быстротоки, нагорные и водоотводные канавы и т. д.);

• решения задачи распределения земляных масс и подсчеты объемов земляных работ;

• решение задач вертикальной планировки при проектировании площадей, городских улиц и дорог и аэродромов;

• пространственное моделирование полотна автомобильных дорог и прилегающего ландшафта. Решение этой задачи широко используют при ландшафтном проектировании автомобильных дорог для обеспечения зрительной плавности и ясности трассы и обеспечения гармоничного вписывания полотна автомобильных дорог в прилегающий ландшафт с обеспечением высоких уровней удобства и безопасности движения;

• проектирование транспортных развязок автомобильных дорог в одном и разных уровнях.

Развитие и совершенствование методов цифрового и математического моделирования местности во многом предопределили и повлияли на изменение технологии и методов изысканий и проектирования объектов инженерного строительства, и дальнейший прогресс проектно-изыскательского дела невозможен без широкого использования в ходе выработки проектных решений, их оценки и корректировки цифровых и математических моделей местности.