Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Кавказский горно-металлургический технологический университет (СКГМИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Грунты(ответы).docx

Скачиваний:

Добавлен:

01.07.2025

Размер:

533.37 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

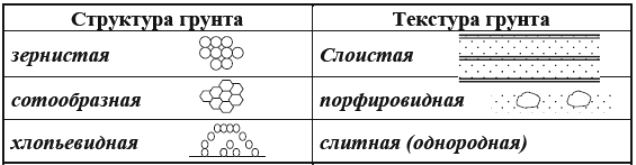
5. Структура, текстура грунта

Следует различать структуру грунта, т. е. взаимное расположение частиц грунта и характер связи между ними, и текстуру грунта, т. е. сложение грунта в массиве.

В дисперсных пылевато-глинистых грунтах, являющихся сложением минерально-дисперсных образований, прочностные свойства зависят не столько от прочности отдельных минеральных зерен, сколько от структурных особенностей грунта. Они обусловливаются структурными связями между минеральными частицами и их агрегатами, а также силами молекулярного взаимодействия между поровой водой и твердыми частицами.

Основными видами структурных связей в грунтах являются водно-коллоидные (коагуляционные и конденсационные) – вязкопластичные, мягкие, обратимые икристаллизационные – хрупкие (жесткие), необратимые; последние могут быть водостойкими и неводостойкими (размягчаемыми и растворимыми).

Водно-коллоидные связи обусловливаются электромолекулярными силами взаимодействия между пленочной водой и твердыми частицами, включая коллоидные частицы. Чем тоньше пленки воды (меньше влажность), тем эти силы больше, и наоборот. Обратимость водно-коллоидных связей заключается в том, что при увлажнении они ослабляются, а при повторном подсушивании опять возрастают. Ослабление водно-коллоидных связей в некоторых случаях наблюдается и при перемятии (нарушении природной структуры). Однако после прекращения перемятия (оставления в покое) такого тиксотропного грунта водно-коллоидные связи в нем постепенно восстанавливаются.

Кристаллизационные связи, образовавшиеся в результате отложения поликристаллических соединений в точках контактов минеральных частиц грунта, обладают достаточно высокой прочностью. Их прочность зависит от состава минералов цементирующего вещества. Связи, образуемые гипсом и кальцитом, существенно снижают свою прочность при увлажнении; связи же, например, из оксидов железа, кремния – водостойки. Кристаллизационные связи хрупкие и не восстанавливаются после их нарушения.

Текстурой грунтов называется их сложение, т. е. пространственное размещение и взаимное расположение частиц грунтов и их агрегатов, зависящее от условий накопления осадка. Например, в озерах ледникового периода образовывались пылевато-глинистые отложения с характерной слоистой тексту- рой. Они представляют собой чередующиеся тонкие слои из глинистых частиц, выпадавших в зимний период подо льдом, и из пылеватых песчаных частиц, оседавших в теплый период года. Различают слоистую, слитную и сложную текстуру:

- слоистая – наиболее распространенный вид сложения грунтов, характерный для морских, озерных и других отложений;

- слитная присуща морским отложениям, имеющим однородное сложение в различных точках массива;

- сложная – порфировая, ячеистая, макропористая и др. (порфировой текстурой обладают моренные суглинки; ячеистая текстура характерна для вечномерзлых грунтов, имеющих вертикальные и горизонтальные полости, заполненные льдом, макропористую текстуру имеют лессовые грунты).

6. Плотностью грунта называется отношение массы грунта к его объѐму при естественном сложении и естественной влажности. Плотностью минеральной части грунта называется отношение массы твѐрдых частиц грунта к их совокупному объѐму. Влажностью грунта называют отношение веса воды в грунте к весу высушенного грунта, выражается в %. Коэффициентом пористости грунта называется отношение объѐма пор грунта к объѐму его скелета. Коэффициент водонасыщенности равен тношению естественной влажности грунта к влажности, соответствующей полному заполнению пор водой (без пузырьков воздуха), т. е. к полной влагоемкости. Характеристики пластичности пылевато-глинистых грунтов — это влажности на границах текучести w_L и раскатывания w_p, определяемые в лабораторных условиях, а также число пластичности I_p и показатель текучести (консистенции) I_L вычисляемые по формулам: Граница текучести – влажность грунта, находящегося м/у пластичным и текучим состоянием. Граница пластичности - влажность грунта, находящегося м/у твердым и пластичным состоянием.

7. Классификация грунтов позволяет не только определить данный грунт, т.е. выделить его среди многообразия других грунтов, но и часто установить ориентировочные значения его прочностных и деформационных характеристик. Действительно, прочность и деформируемость грунтов непосредственно связаны с их физическими свойствами и состоянием. Например, увеличение пористости песчаного и пылевато-глинистого грунта (увеличение коэффициента пористости) при прочих равных условиях непременно влечет за собой снижение его прочности и повышения деформируемости. Соответственно увеличение влажности (показателя консистенции) глинистого грунта, также при прочих равных условиях, приведет к снижению его прочности и повышению дефомируемости. Следовательно, установление связей между физическими и механическими характеристиками грунтов в определенных условиях правомочно. Так, в частности, основываясь на обобщении огромного количества испытаний, СНиП 2.02.01-83 допускает для предварительных расчетов оснований, а также для окончательных расчетов оснований зданий и сооружений II и III классов и опор возводимых линий электропередачи и связи независимо от их класса определять нормативные и расчетные значения прочностных и деформационных характеристик грунтов по их физическим характеристикам. С этой целью в СНиПе приводятся таблицы нормативных значений прочностных и деформационных характеристик некоторых разновидностей песчаных и пылевато-глинистых грунтов и значения соответствующих коэффициентов надежности по грунту. Важной характеристикой несущей способности является р а с ч е т н о е с о п р о т и в л е н и е грунтов основания Rₒ (кПа), ориентировочно допустимое давление на данный грунт под подошвой фундамента, имеющего ширину 1 м и глубину заложения 2м.

СНиП 2.02.01 – 83 допускает назначать предварительные размеры фундаментов исходя из этой величины. Кроме того, значение величины Rₒ для различных слоев при сложном напластовании позволяет на ранней стадии изысканий, определив только физические характеристики грунтов, провести приблизительную сопоставительную оценку их несущей способности.

Свойства грунтов	Закономерности	Показатели	Где применяется закономерность
Сжимаемость	Закон уплотнения (компрессии)	Коэффициент сжимаемости (уплотнения) (т0)	Расчет осадок фундаментов
Прочность	Закон сопротивления грунта сдвигу (закон Кулона)	Коэффициент внутреннего трения (<р) и сцепления (с)	Расчет предельной прочности, устойчивости и давления на ограждения
Водопроницаемость	Закон ламинарной фильтрации (закон Дарси)	Коэффициент фильтрации (kf)	Прогноз скорости осадок водонасыщенных грунтовых оснований

9. Сжимаемость грунтов – способность грунтов изменять свое строение (упаковку твердых частиц) под влиянием внешних воздействий на более компактное за счет уменьшения пористости

Для установления основных показателей сжимаемости грунтов производятся их испытания на уплотнение под нагрузкой, когда деформации грунта могут развиваться только в одном направлении и никакие другие силы, кроме внешней нагрузки, не действуют.

Для испытания грунтов на сжимаемость применяются приборы с жесткими стенками (одометры) для обеспечения сжатия грунта только в одном направлении (без возможности бокового расширения).

Закон уплотнения: бесконечно малое изменение относительного объема пор грунта прямо пропорционально бесконечно малому изменению давления.

10. Коэффициентом бокового давления покоя следует называть коэффициент бокового давления для грунта в стабилизированном состоянии при неизменном положении вертикальных сечений образца и отсутствии касательных напряжений по ним.

Коэффициент бокового давления покоя ξ грунта определяется из отношения бокового давления σ₂ = σ₃ к нормальному давлению σ₁:

ξ = σ₂/σ₁. (1)

Нормальное давление следует задавать исходя из условий работы грунта основания в интервале давлений, соответствующих давлению, эквивалентному природному σ_э или давлению, соответствующему структурной связности σ_стр*, и заданному проектному давлению.

Боковое давление определяется из опыта в стабилометре с применением аэростатического манометра (капиллярная трубка). Боковое давление вычисляется по формуле:

σ₂ = σ₀(L₀/L_i - 1), (2)

где σ₂ - давление в капилляре, равное боковому давлению в образце, в МПа;

σ₀ - атмосферное давление в МПа;

L₀ - длина столбика воздуха до опыта при атмосферном давлении;

L_i - длина столбика воздуха после сжатия в конце опыта.

1.5. Коэффициент поперечного расширения μ определяется из отношения приращения относительной поперечной деформации l_r = l_θ к приращению относительной вертикальной деформации l_z при постоянной нормальной нагрузке σ_z и при условии допущения равномерного расширения образца по высоте:

μ = l_r/l_z. (3)

Нормальное давление в опыте должно быть больше σ_стр и меньше разрушающего. Вертикальные деформации грунта измеряются по перемещению штампа. Поперечное расширение l_r = l_θ рекомендуется измерять по количеству вытесненной жидкости из гидравлической камеры в волюмометр и, принимая, что поперечные деформации пропорциональны изменению уровня жидкости ∆h в волюмометре, вычислять по формуле:

(4)

где f - площадь трубки волюмометра;

∆h - изменение положения мениска в волюмометре;

R₀ - радиус образца до опыта;

H - высота образца до опыта.

1.6. Коэффициенты бокового давления и поперечного расширения связаны между собой зависимостями:

ξ = μ/(1 - μ); (5)

μ = ξ/(1 + ξ). (6)

Следует иметь в виду, что эта зависимость справедлива для случая, когда главные деформации l₂ = l₃ = 0. Для случая осесимметричной деформации, когда l₂ = l₃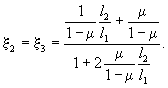

11. Водопроницаемость – способность фильтровать воду. Скорость напорного движения грунтовых вод зависит от размеров пор грунта, сопротивлений по пути фильтрации и величины действующих напоров (илл.5).

Илл. 5. Напорные грунтовые воды

Здесь Н₁ и Н₂ – напоры; L – длина пути фильтрации; Н = Н₂ - Н₁ – потеря напора или «действующий напор». Если линии токов воды (движения частиц в потоке) нигде не пересекаются друг и другом, то такое движение называется ламинарным, при наличии пересечений и завихрений движение называется турбулентным. В грунтах в большинстве случаев движение воды будет ламинарным (опыты Пуазейля, Дарси и другие).

Ламинарное движение воды происходит с тем большей скоростью, чем больше уклон поверхности уровня грунтовых вод (так называемый «гидравлический градиент»).

Гидравлический градиент равен отношению потери напора Н= Н₂- Н₁ к длине пути фильтрации L:

Закон ламинарной фильтрации: расход воды в единицу времени через единицу площади поперечного сечения грунта (скорость фильтрации) прямо пропорционален гидравлическому градиенту i:

v_ф = k_ф · i;

где k_ф - коэффициент фильтрации, равный скорости фильтрации при градиенте i = 1 [см/сек, см/год]. Коэффициент фильтрации зависит от типа грунта и определяется экспериментально.

Зависимость скорости фильтрации от гидравлического градиента i. Для водопроницаемых грунтов (пески, галечники) зависимость прямая (илл. 6).

Илл. 6. Зависимость скорости фильтрации от гидравлического градиента

Фильтрация воды в глинистых грунтах начинается при достижении некоторой начальной величины градиента i, преодолевающей внутреннее сопротивление движению, оказываемое водно-коллоидными пленками. На рисунке (илл.6) изображены экспериментально найденные зависимости скорости фильтрации v_ф от гидравлического градиента i. Здесь i₀ - начальныйгидравлический градиент

В результате закон ламинарной фильтрации для связных грунтов будет иметь вид: v_ф = k_ф · (i – i₀).

12. Суффозия заключается в вымывании частиц грунта движущимся потоком воды.

Кальматация — это отложение мелких частиц вблизи открытой поверхности, вызывающее уменьшение пористости и снижение водонепроницаемости. Эффективное напряжение и поровое давление. эффективное напряжение в скелете грунта может быть выражено через полное напряжение и поровое давление: = σ– U_w_.Опытами Л. Рендулика было показано, что эффективное напряжение, действуя в контактах между частицами скелета грунта, приводит в конечном счете к частичному разрушению скелета, сопровождающемуся уплотнением грунта. Поровое давление развивается только в воде, не оказывает воздействия на скелет грунта, т. е. yе приводит к его уплотнению, а создает лишь дополнительный вапор в воде, вызывающий ее фильтрацию, поэтому его иногда называют нейтральным давлением.

Таким образом, фильтрация воды в грунте возникает не только в результате разности пьезометрических напоров,но и под действием напоров, обусловленных разницей порового давления в различных точках основания, воспринимающего нагрузку от сооружения. Этот механизм положен в основу математического аппарата теории фильтрационной консолидации грунта.

13. Для изучения предельного сопротивления грунтов сдвигу, разработаны специальные приборы и методики испытаний. Наиболее распространенными в настоящее время являются сдвиговые приборы.

Существует много конструктивных разновидностей сдвиговых приборов, среди которых можно выделить две группы: 1) приборы со ступенчатым загружением; 2) приборы с непрерывным загружением.

Испытанию подвергаются образцы грунта с ненарушенной структурой, иногда с нарушенной структурой, иногда с нарушенной с заданными исходными значениями плотности, влажности (напр. для песков). Образец грунта помещается в металлическое кольцо, разделенное на части — подвижную и неподвижную обоймы. Подвижной может быть как нижняя, так и верхняя обоймы между обоймами до проведения опыта устанавливается небольшой зазор, который необходимо сохранять в течении всего опыта. Таким образом, создается фиксированная плоскость, по которой произойдет срез подвижной части грунта относительно неподвижной. Вертикальное нормальное напряжение в плоскости сдвига создается с помощью рычажной системы в предположении, что нормальные напряжения в плоскости сдвига распределены равномерно, т. е. Вертикально приложенной силе, деленной на площадь образца. Нормальное напряжение сохраняется в течении всего опыта постоянным. Образец грунта до приложения сдвигающей силы обжимается некоторое время, зависящее от вида грунта, нормальным приложением Ϭ=Ϭ'=0,1 мПа. Будем теперь в подвижной обойме отдельными ступенями прикладывать сдвигающую силу τ через соответствующую рычажную систему. Под действием приложенной ступени горизонтальной сдвигающей силы подвижная часть грунта начнет перемещаться относительно подвижной. За величиной перемещения наблюдают с помощью специальных измерителей (индикаторов часового типа). Предельное сопротивление грунта сдвигу выражается в виде предельных касательных напряжений τ_пр=f(Ϭ) и определяется на приборах непрерывного нагружения. По результатам испытаний строят диаграмму, откладывая по вертикальной оси предельное сдвигающее напряжение τ, а по горизонтальной Ϭ уплот. Давление.

Предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению.

Предельное сопротивление сдвигу связных грунтов при завершенной их консолидации есть функция первой степени от нормального давления (сжимающего напряжения)

15. Недоуплотненные грунты – грунты, у которых при незавершенной консолидации образовались структурные связи, препятствующие их дальнейшему уплотнению. Просадки – местные, быстро протекающие осадки недоуплотненных структурно-неустойчивых грунтов, обусловленные резким изменением их структуры, сопровождаются выдавливанием текучепластичных масс в сторону от местного воздействия. Грунты с такими свойствами – просадочные. Это лессовые грунты при замачивании под нагрузкой, сильнольдистые мерзлые и вечномерзлые при оттаивании; органо – минеральные илы при быстром нагружении; рыхлые слабые пески – при воздействии вибраций.

Просадочность грунтов оценивается относительной просадочностью:

где h_p – высота образца ненарушенной структуры; h¢_p – его же высота, при воздействии р > р_стр

e_пр ³ 0,02 – просадочные

При р = 0,2 – 0,25 МПа для лессовых при замачивании и р = 0,25 – 0,4 МПа мерзлые и вечномерзлые при оттаивании:

e_пр = А_о + m_dр,

где А_о – коэф-т просадки лессовых и коэф-т оттаивания мерзлых и вечномерзлых грунтов; m_d - угловой коэф-т прямой, характеризующий относит. сжимаемость в процессе просадки.

14. Многочисленные исследования показывают, что зависимость между напряжениями и деформациями нелинейна, и в общем виде ее можно записать как

e = a_c s_c+ a _n(s_n -s_c)^m, (2.61)

где a_c и a_n – коэффициенты, определяемые опытом; s_c – напряжение, не превышающее структурной прочности грунта s_c£P_стр; s_n – напряжения, обусловливающие деформации грунта, s_n-s_c=s; m – параметр нелинейности, определяемый опытным путем.

Коэффициент a_c обратно пропорционален модулю упругости:

Коэффициент a_n зависит от модуля общей деформации E₀:

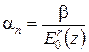где b – коэффициент, зависящий от коэффициента Пуассона; r – параметр, меньший или равный единице, определяется также опытным путем.

При давлениях больше структурной прочности формулу (2.60) можно записать так:

, (2.62)

где a_cn – общий коэффициент пропорциональности,

Фаза уплотнения соответствует уровням напряжений в грунте, в диапазоне которых процесс его деформирования удовлетворительно подчиняется закону уплотнения Терцаги. Линейная зависимость между деформациями и напряжениями в этой фазе не является обратимой. При разгрузке штампа из диапазона давлений, соответствующего фазе уплотнения, грунт деформируется по линейной зависимости, не совпадающей с ветвью нагрузки. При полной разгрузке штампа (рис. 1.5) имеет место необратимая (пластическая) осадка, соответствующая нулевым напряжениям по подошве. Повторное нагружение штампа до уровня напряжений, достигнутых перед разгрузкой, происходит по графику, совпадающему с графиком разгрузки. Нагружение выше этого уровня происходит по закону первичной нагрузки. Таким образом, закон уплотнения Терцаги устанавливает линейную зависимость между напряжением и суммой упругой и пластической деформации грунта. Указанная особенность закона уплотнения формулируется как принцип линейной деформируемости: при простом нагружении грунта в фазе его уплотнения сумма упругой и пластической деформации линейно зависит от действующего напряжения. Коэффициентом пропорциональности в этой линейной зависимости является модуль деформации грунта Е, названный так в отличие от модуля упругости, характеризующего деформацию упругого тела. Модуль упругости грунта Е_е определяется по графику разгрузки и является коэффициентом пропорциональности между упругой деформацией грунта и действующим напряжением. Модуль деформации используется в статических расчетах, а модуль упругости – в динамических расчетах грунтовых оснований.

Фаза сдвигов характеризует начало образования в грунте зон предельного равновесия. Зоной предельного равновесия в грунте называют геометрическое место точек, в которых не удовлетворяются условия прочности Кулона – Мора. Первоначально эти зоны образуются по краям штампа, где имеет место концентрация напряжений. Разрушение грунта сопровождается большими сдвиговыми деформациями, что нашло отражение в названии рассматриваемой фазы напряженно-деформированного состояния грунта. Уплотнение грунта в этой фазе практически не происходит. Грунт считается несжимаемым, а коэффициент Пуассона в этой фазе близок к 0,5. Давление на грунт, соответствующее началу фазы сдвигов, называют начальным критическим давлением –^нач.р_кр.

Фаза выпора является следствием развития фазы сдвигов в области грунтового массива, являющегося основанием штампа, с образованием поверхностей скольжения, отделяющих основание штампа от нижележащего грунтового массива. В результате этого осадки штампа происходят без увеличения нагрузки за счет перемещения грунта основания из-под штампа по плоскостям скольжения с выходом на поверхность грунтового массива. При этом вокруг штампа происходит поднятие (выпор) грунта, что нашло отражение в названии этой фазы. Непосредственно под штампом в фазе выпора образуется коническая переуплотненная зона, называемая ядром жесткости. Прочность этой зоны обусловлена боковыми давлениями со стороны окружающего грунта, находящегося в состоянии пластического течения. Как известно, коэффициент бокового давления в грунте в состоянии пластического течения стремится к единице. Таким образом, жесткое ядро находится до исчерпания несущей способности основания в состоянии компрессионного сжатия, близкого к трехосному сжатию, что и определяет его высокую прочность. В зонах пластического течения недоуплотненные грунты получают дополнительное уплотнение, а переуплотненные – разуплотняются. Это явление называется дилатансией. Давление, при котором наступает фаза выпора, называется предельным критическим давлением – ^пред.р_кр.

16. Лессовые породы представлены суглинками, реже—супесями. Среди них различают лесс (первичное образование) и лессовидные суглинки (переотложенные первичные образования). Гранулометрический состав их нередко бывает сходным, поэтому в строительном целесообразно пользоваться единым названием "лессовые грунты" подразделяя их по гранулометрическому составу на супеси, суглинки, глины. Для лессов типична однородность. Лессовидные суглинки обычно слоисты и могут содержать обломки различных пород. Лессовые грунты бывают палевой, палево-желтой или желто-бурой окраски. Для них характерны следующие особенности: способность сохранять вертикальные откосы в сухом состоянии, быстро размокать в воде, высокая пылеватость (содержание фракции 0,05—0,005 мм более 50% при небольшом количестве глинистых частиц), невысокая природная влажность (до 15—17%); пористая структура (более 40%) с сетью крупных и мелких пор, высокая карбонатность, засоление легко водорастворимыми солями. Просадка проявляется уже как дополнительное к осадке уплотнение. Таким образом, деформация породы складывается из «осадки — просадки». Для конкретных условий эта величина обычно постоянная. Соотношение между осадкой и просадкой может меняться. В более сухих грунтах осадка будет уменьшаться, а просадка возрастать, и наоборот.

Все методы подразделяют на три группы: 1) водозащитные; 2) конструктивные; 3) устраняющие просадочные свойства пород.

Водозащитные мероприятия предусматривают планировку строительных площадок для отвода поверхностных вод, гидроизоляцию поверхности земли, предохранение зданий от утечек воды из водопроводов, устройство водонепроницаемых полов, покрытий, отмосток и т. д. Конструктивные мероприятия рассчитаны на приспособление объектов к возможным неравномерным осадкам, повышение жесткости стен и прочности стыков, армирование зданий поясами, применение свайных, а также уширенных фундаментов, передающих давление на фунт меньше, чем P_SL- Маломощные просадочные грунты (H_SL) прорезаются глубокими фундаментами, в том числе свайными.

Наибольшее число методов связано с устранением просадочных свойств. Их подразделяют на две группы:

• улучшение пород с применением механических методов;

• физико-химические способы улучшения.

Механические методы преобразуют породы либо с поверхности, либо в глубине толщ. Поверхностное уплотнение производят трамбовкой, замачиванием под своим весом или весом сооружения. В глубине толщ уплотнение производят с помощью грунтовых свай (песчаных, известняковых), взрывов в скважинах, замачиванием через скважины с последующим взрывом под водой и т. д. Находят применение также песчаные и грунтовые подушки, грунто-цементные опоры.

17. Грунты всех видов относят к мерзлым грунтам, если они имеют отрицательную температуру и содержат в своем составе лед.

Вечномерзлыми называют грунты, которые находятся в мерзлом состоянии непрерывно в течение многих лет (трех и более).

Мерзлые и вечномерзлые грунты в естественном состоянии при отрицательной температуре являются очень прочными и малодеформируемыми грунтами.

При замораживании и оттаивании вечно мерзлые грунты меняют свои структурные свойства. Основной особенностью таких грунтов являются их просадочность при оттаивании.

18. Структурно-неустойчивыми называют такие грунты, которые обладают способностью изменять свои структурные свойства под влиянием внешних воздействий с развитием значительных осадок, протекающих, как правило, с большой скоростью. К основным воздействиям относятся увлажнение грунтов, промерзание и оттаивание, суффозия и выветривание, внешние нагрузки, перемятие грунтов и др. Такое название они получили потому, что при определенных условиях их природная структура сравнительно резко нарушается. К структурно-неустойчивым относятся следующие грунты:

- лессовые, структура которых нарушается при замачивании их под нагрузкой;

- набухающие, которые при увлажнении способны существенно увеличиваться в объеме даже под нагрузкой;

- засоленные, песчано-глинистые отложения, в которых накопление солей произошло в процессе их формирования

сильносжимаемые грунты, деформационные и прочностные свойства которых резко изменяются при нарушении их природной структуры;

- торфы и заторфованные грунты, обладающие очень большой сжимаемостью и малой прочностью;

- мерзлые и вечномерзлые, структура которых нарушается при оттаивании.

19. Требуеться определить все компоненты нормальних Ϭ и касательных напря жений τ а также перемещений w для любой точки полупространства с коор динатами x, y,z или R и β в полярной системе. В какой то точке М , определяемой полярними координатами β

и R действует нормальное напряжение ϬR по направлению радиуса R. Согласно решения Буссинеска его величина определяется выражением:

ϬR =А(cosβ )/R2

Здесь А-коэфициент, определяемый из условия равновесия, корда сумма проекцій всех сил на вертикальную ось ровна нулю. В результате

получим что А=( 3/2)(Р/π ).

В результате получим, что

ϬR=(3/2)(Р/π R2 ).cosβ

Рассмотрим величину радиального напряжения действующего на площадке паралельной ограничивающей полупространство плоскости

и направленого по радиусу R и под углом β к линии действия Р и обозначим его как ϬRI (Рис.3.3. Ц2 ст 79).,видно что

ϬRI=ϬR cosβ

cosβ=z/R

ϬRI=(3/2)(P/π)(z2 /R4)

Раскладывая данное напряжение на три направления: Z,X иY получим, что

Ϭz =( 3/2)(P/π)(z3/R5)

τzy=(3/2)(P/π)(z3/R5) ( 3.1.)

τzx=(3/2)(P/π)(xz2/R5)

Сумма нормальних напряжений в любой точке ϴ и перемещений wz определяються выражениями:

ϴ=Ϭz + Ϭy + Ϭx= Ϭ1 +Ϭ2 + Ϭ3 =P/π(1+μ0) z/R3 ( 3.2/)

wz=P/ π CR (3.3.)

Здесь C=E0 / (1+ μ02 )- коэфициент линейнодеформируемого полупространства,E0 –модуль общей деформации, μ0 –коэфициент Пуассона,

Положение точки М на Рис.3.3.опаределяеться двумя её координатами: z и r но так как

R=( z2+r2)1/2=z(1+(r/z)2 )

То на основании одной из формул (3.1.) можно получить:

Ϭz =K(P/z2) (3.4.)

Здесь K=(3/2 π) 1/(1+ (r/z)2 )5/2

Значения К для любих точек плоупространства приводяться в справочных таблицях, например у Титовича.

Если к поверхности приложено несколько сосредоточенных сил Р1 тогда напря жения определяються по формуле:

Ϭz=K1P1/ z2+ K2P2/z2+ K3 P3 / z2 (3.5.)

Здесь коэфициент К каже определяется по таблицям в зависимости от значений отношения ri / z .

20. Этот случай соответствует напряженному состоянию под стеновыми фундаментами, подпорными стенками, насыпями и другими сооружениями, длина которых значительно превосходит их поперечные размеры:

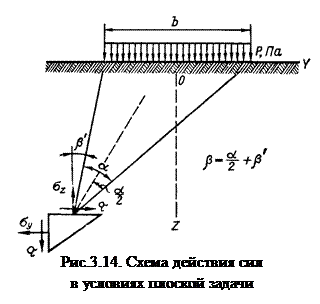где l – длина фундамента; b – ширина фундамента. При этом распределение напряжений под любой частью сооружения, выделенной двумя параллельными сечениями, перпендикулярными оси сооружения, характеризует напряженное состояние под всем сооружением и не зависит от координат, перпендикулярных к направлению загруженной плоскости.

Рассмотрим действие погонной нагрузки в виде непрерывного ряда сосредоточенных сил Р, каждая из которых приходится на единицу длины. В этом случае составляющие напряжений в любой точке М с координатами R и b могут быть найдены по аналогии с пространственной задачей:

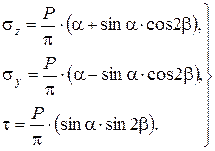(3.27)

Если соотношения геометрических характеристик рассматриваемых точек z, y, b представить в виде коэффициентов влияния K, то формулы для напряжений можно записать так:

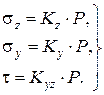(3.28)

Значения коэффициентов влияния K_z, K_y, K_yz табулированы в зависимости от относительных координат z/b, y/b (табл. II.3 приложения II).

Важное свойство плоской задачи в том, что составляющие напряжений t и s_y в рассматриваемой плоскости z0y не зависят от коэффициента поперечного расширения n₀, как в случае пространственной задачи.

Задача может быть решена и для случая погонной нагрузки, любым образом распределенной по полосе шириной b. При этом элементарную нагрузку dP рассматривают как сосредоточенную силу (рис.3.15).

Рис.3.15. Произвольное распределение

нагрузки по ширине полосы b

Если нагрузка распространяется от точки A(b=b₂) до точки B(b=b₁), то, суммируя напряжения от ее отдельных элементов, получим выражения для напряжений в любой точке массива от действия сплошной полосообразной нагрузки.

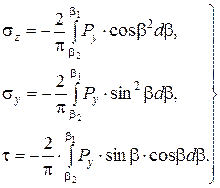(3.29)

Этот случай соответствует напряженному состоянию под стеновыми фундаментами, подпорными стенками, насыпями и другими сооружениями, длина которых значительно превосходит их поперечные размеры: