
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Національний університет «Львівська політехніка»

Інтерполяційні поліноми Ньютона
для рівновіддалених вузлів
Завдання та методичні рекомендації
до лабораторної роботи № 6 з курсу
«Чисельні методи»
для базового напрямку 040204 «Прикладна фізика»
Затверджено
на засіданні кафедри
обчислювальної математики та програмування
Протокол № 5 від 30.01.2012 p.
ЛЬВІВ – 2011
Інтерполяційні поліноми Ньютона для рівновіддалених вузлів. Завдання та методичні рекомендації до лабораторної роботи № 6 з курсу «Чисельні методи» для базового напрямку 040204 «Прикладна фізика» / Укл. Я.М.Глинський, Н.М.Гоблик, З.О.Гошко, В.А.Ряжська, 2012. – 11 с.
Укладачі: Глинський Я.М., канд. фіз.-мат. наук, доц.
Гоблик Н.М., ст. викл.
Гошко З.О., асистент
Ряжська В.А., канд. фіз.-мат. наук, доц.
Відповідальна за випуск Ряжська В.А., канд. фіз.-мат. наук, доц.
Рецензент доктор фіз.-мат. наук, проф. Чабанюк Я.М.
Передмова
У методичних вказівках розглянуто побудову інтерполяційного полінома Ньютона для рівновіддалених вузлів для заданої таблично функції.
Методичні вказівки містять короткі теоретичні відомості, приклад побудови інтерполяційного полінома Ньютона для рівновіддалених вузлів для заданої таблично функції, обчислення його похибки у заданих точках, а також індивідуальні завдання для самостійної роботи студентів. Приклад розв’язаний як вручну, так і у середовищі MatLab
Методичні вказівки призначені для студентів базового напрямку 040204 «Прикладна фізика» і укладені відповідно до робочої програми курсу «Чисельні методи».
1. Мета роботи
Мета роботи – навчитись будувати інтерполяційні поліноми Ньютона для рівновіддалених вузлів для заданої таблично функції і знаходити її значення в довільній точці.
2. Теоретичні відомості
Задача.
Нехай відомі значення
 функції
функції
 у
у
 і нехай вузли
і нехай вузли
 рівновіддалені один від одного, тобто
рівновіддалені один від одного, тобто
 ,
де
,
де
 – величина кроку інтерполяції.
– величина кроку інтерполяції.
Потрібно знайти значення функції у довільній точці.
Введемо означення скінченної різниці.
Скінченною різницею першого порядку називають величину
 ,
,
де
 – різниця вперед, а
– різниця вперед, а
 – різниця назад;
– різниця назад;
Скінченною різницею k – го порядку називають величину
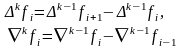 .
.
Інтерполяційним поліномом Ньютона для інтерполювання вперед в околі точки х називають поліном
 ,
,
де
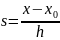 .
.
Цю
формулу зручно використовувати, якщо
точка х
знаходиться ближче до точки
 .
.
Інтерполяційний поліномом Ньютона для інтерполювання вперед інакше називають першим інтерполяційним поліномом Ньютона чи інтерполяційним поліномом Ньютона першого роду.
Якщо
у формулі Ньютона інтерполяційні вузли
перенумерувати у порядку
 і зробити заміну
і зробити заміну
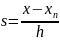 ,
то отримаємо інтерполяційний многочлен
,
то отримаємо інтерполяційний многочлен
 ,
,
який
називають інтерполяційним
многочленом Ньютона для інтерполювання
назад
і використовують якщо точка х
знаходиться ближче до точки
 .
.
Приклад.
Побудувати інтерполяційний многочлен
Ньютона
 для таблично заданої функції f(x)
та обчислити його значення у точках
х = 0,12
та х = 0,94.
Оцінити похибку обчислень.
для таблично заданої функції f(x)
та обчислити його значення у точках
х = 0,12
та х = 0,94.
Оцінити похибку обчислень.
і |
0 |
1 |
2 |
3 |
4 |
5 |
хі |
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
f(xi) |
–2,000 |
–1,940 |
–1,763 |
–1,476 |
–1,090 |
–0,621 |
Для оцінки похибки скористатись формулою i = | f(xi) - L(xi)|, де i = 1, 2, якщо f(x) = –3cosx + 1.
Розв’язання. Побудуємо таблицю скінченних різниць
i |
хі |
f(xi) |
|
|
|
|
|
0 |
0 |
- 2,000 |
0,060 0,177 0,287 0,386 0,469 |
0,117 0,110 0,099 0,083 |
-0,007 -0,011 -0,015 |
-0,004 -0,004 |
0,000 |
1 |
0,2 |
- 1,940 |
|||||
2 |
0,4 |
- 1,763 |
|||||
3 |
0,6 |
- 1,476 |
|||||
4 |
0,8 |
-1,090 |
|||||
5 |
1 |
-0,621 |
Оскільки
точка х = 0,12
знаходиться в околі точки
,
то скористаємось інтерполяційним
поліномом Ньютона для інтерполювання
вперед. Отримаємо тоді
тоді
 ,
,
Отже, L4(0,12) = –1,654.
Значення заданої функції в цій точці дорівнює
f(0,12) = –3cos(0,12) + 1 = –1,978.
Тоді похибка
= |–1,978 – (–1,654)| = –0,324.
Для точки х = 0,94 побудуємо інтерполяційний поліном для інтерполювання назад. Тут


Звідси L4(0,94) = –0,769, функція f(0,94) = –3cos(0,94)+ 1 = –0,769, а похибка = 0.
Розв’язання в середовищі MATLAB.
1) Файл newton1.m
function yy=newton1(x,y,t,n0)
%перша інтерполяційна формула Ньютона для рівновіддалених вузлів(інтерполяція вперед)
% обчислення значення інтерполяційного полінома у формі Ньютона в точці t
%x-вектор значень х
%y-вектор значень функції
%n0-номер точки в масиві х, яка найближча до t
% yy - значення полінома в точці t
N=length(x)-1
%формування масивy різниць значень функції
deltay(:,1)=y;
k=N;
for nn=2:N
for j=1:k
deltay(j,nn)= deltay(j+1,nn-1)- deltay(j,nn-1);
end
k=k-1;
end
h=mean(diff(x)) %обчислення кроку
q=(t-x(n0))/h;
s=y(n0);
p=q;
fact=1;
for i=2:N
s=s+p*deltay(n0,i)/fact;
fact=fact*i;
p=p*(q-1);
end
yy=s;
Обчислення значення функції в точці х=1,1:
>> x=1:0.1:2;
>> y=-3*cos(x)+1;
>> t=1.1;
>>n0=1;
>> yy=newton1(x,y,t,n0)
yy =
-0.3608
Перевірка:
>> -3*cos(t)+1
ans =
-0.3608
2) Файл newton2.m
function yy=newton2(x,y,t,n0)
%друга інтерполяційна формула Ньютона для рівновіддалених вузлів(інтерполяція назад)
% обчислення значення інтерполяційного полінома у формі Ньютона в точці t
%x-вектор значень х
%y-вектор значень функції
%n0-номер точки в масиві х, яка найближча до t
% yy - значення полінома в точці t
N=length(x)-1
%формування масивy різниць значень функції
deltay(:,1)=y;
k=N;
for nn=2:N
for j=1:k
deltay(j,nn)= deltay(j+1,nn-1)- deltay(j,nn-1);
end
k=k-1;
end
h=mean(diff(x)) %обчислення кроку
q=(t-x(n0))/h;
s=y(n0);
p=q;
fact=1;
for i=2:N
s=s+p*deltay(n0-1,i)/fact;
fact=fact*i;
p=p*(q+1);
n0=n0-1;
end
yy=s;
Обчислення значення функції в точці х=1,8:
>> x=1:0.1:2;
>> y=-3*cos(x)+1;
>> t=1.8;
>> n0=11;
>> yy=newton2(x,y,t,n0)
yy =
1.6826
Перевірка:
>> -3*cos(t)+1
ans =
1.6816





