МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Національний університет «Львівська політехніка»

Прямі методи розв’язування

систем лінійних алгебраїчних рівнянь (СЛАР)

Завдання та методичні рекомендації

до лабораторної роботи № 3 з курсу

«Чисельні методи»

для базового напрямку 040204 «Прикладна фізика»

Затверджено

на засіданні кафедри

обчислювальної математики та програмування

Протокол № 5 від 30.01.2012 p.

ЛЬВІВ – 2011

Прямі методи розв’язування систем лінійних алгебраїчних рівнянь (СЛАР). Завдання та методичні рекомендації до лабораторної роботи № 3 з курсу «Чисельні методи» для базового напрямку 040204 «Прикладна фізика» / Укл. Я.М.Глинський, Н.М.Гоблик, З.О.Гошко, В.А.Ряжська, 2012. – 13 с.

Укладачі: Глинський Я.М., канд. фіз.-мат. наук, доц.

Гоблик Н.М., ст. викл.

Гошко З.О., асистент

Ряжська В.А., канд. фіз.-мат. наук, доц.

Відповідальна за випуск Ряжська В.А., канд. фіз.-мат. наук, доц.

Рецензент доктор фіз.-мат. наук, проф. Чабанюк Я.М.

Передмова

У методичних вказівках розглянуто точні методи розв’язування систем лінійних алгебраїчних рівнянь.

Методичні вказівки містять короткі теоретичні відомості, приклади розв’язування систем лінійних алгебраїчних рівнянь за допомогою методів оберненої матриці, Гауса та Халецького, а також індивідуальні завдання для самостійної роботи студентів. Кожен приклад розв’язаний як вручну, так і у середовищі MatLab

Методичні вказівки призначені для студентів базового напрямку 040204 «Прик­ладна фізика» і укладені відповідно до робочої програми курсу «Чи­сель­ні методи».

1. Мета роботи

Мета роботи – навчитись знаходити точний розв’язок системи лінійних алгебраїчних рівнянь

2. Теоретичні відомості

Розв’язати систему лінійних алгебраїчних рівнянь (СЛАР)

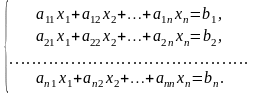
або у векторній формі

Ax = b,

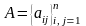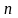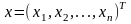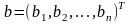де – задана матриця порядку , – невідомий вектор, – за­да­но.

Якщо визначник матриці 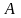відмінний від нуля, то розв’язок системи існує і він єдиний.

Методи чисельного розв’язування систем ділять на два типи: прямі (точні) та ітераційні (наближені). За допомогою прямих (або точних) методів розв’язок СЛАР знаходять за скінченну кількість арифметичних дій.

Метод оберненої матриці

Помножимо праву і ліву частину рівності Ax=b на А^-1, де А^-1 – обернена матриця:

А^-1 Ax = А^-1b.

Отримаємо розв’язок

x = А^-1b.

Приклад 1. Знайти розв’язок системи Ax = b, де

,

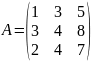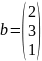
методом оберненої матриці.

Розв’язання. Знайдемо обернену матрицю

,

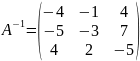тоді

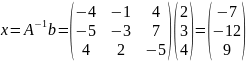
Розв’язання в середовищі MATLAB.

Програма методу оберненої матриці:

function x=ob_m(A,b)

%програма розв'язування системи лінійних алгебраїчних рівнянь

%методом оберненої матриці

%А - матриця коефіцієнтів системи

%b - вектор-стовпець вільних членів

%х - розв'язок

%перевірка, чи існує обернена матриця

d=det(A);

if d==0

error('обернена матриця не існує')

end;

x=A^(-1)*b;

Створення матриці коефіцієнтів системи та вектора-стовпця вільних членів:

>> A=[1 3 5;3 4 8;2 4 7]

A =

1 3 5

3 4 8

2 4 7

>> b=[2 3 1]

b =

2 3 1

>> b=b'

b =

2

3

1

Виклик програми:

>> x=ob_m(A,b)

x =

-7.0000

-12.0000

9.0000

Перевірка розв'язку:

>> A*x

ans =

2.0000

3.0000

1.0000

Метод Гауса

Знайдемо розв’язок системи Ax = b методом Гауса. Для цього послідовно зведемо матрицю А до трикутного вигляду.

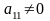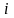Припустимо, що . На першому кроці від -го рівняння системи віднімаємо перше рівняння, помножене на 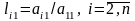. У результаті отримаємо систему

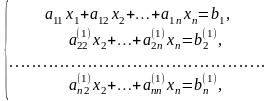
де 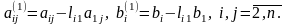Якщо 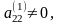то з останніх 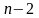рівнянь останньої системи можна виключити

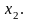
На 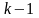кроці прямого ходу матимемо систему рівнянь:

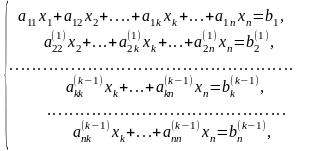
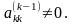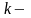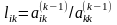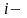Припустимо, що Помножимо те рівняння системи на і віднімемо від го, де 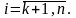Отримаємо

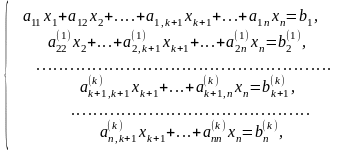
де

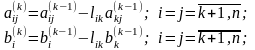
Елемент 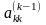на му кроці виключення називають головним елементом.

Після закінчення прямого ходу отримаємо систему рівнянь із верхньою трикутною матрицею:

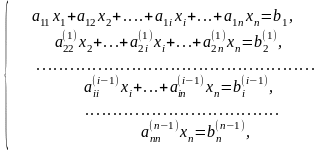
З цієї системи визначимо невідомі 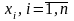за формулами:

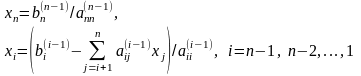
Систему лінійних рівнянь розв’язано.

Приклад 2. Знайти розв’язок системи Ax=b, де

,

методом Гауса.

Розв’язання. Зведемо розширену матрицю системи до трикутного вигляду

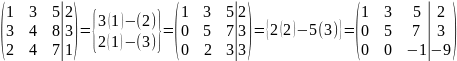
З останнього рівняння знайдемо х₃ = 9, тоді з другого (5х₂+7х₃=3) – х₂ = –12, а з першого знайдемо х₁ = –7.

Розв’язання в середовищі MATLAB.

function x=m_Gaus(A,b)

%програма розв'язування системи лінійних алгебраїчних рівнянь

%методом Гауса

%А - матриця коефіцієнтів системи

%b - вектор-стовпець вільних членів

%х - розв'язок

R=[A b];

r=size(R);

n=r(1) %кількість рядків розширеної матриці

%прямий хід

p=1;

for k=1:n-1

s=R(k,:);

s=s./R(k,p);

R(k,:)=s;

for L=k+1:n

t=s.*R(L,p);

R(L,:)=R(L,:)-t;

end

p=p+1;

end

%зворотній хід

x=zeros(n);

x=x(:,1);

x(n)=R(n,n+1)/R(n,n);

for k=n-1:-1:1

s=0;

for L=k+1:n

s=s+x(L)*R(k,L);

end

x(k)=R(k,n+1)-s;

end

Виклик програми:

>> A=[1 3 5;3 4 8;2 4 7]

A =

1 3 5

3 4 8

2 4 7

>> b=[2 3 1]'

b =

2

3

1

>> x=m_Gaus(A,b)

x =

-7.0000

-12.0000

9.0000

Метод Халецького (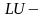 розклад, факторизація).

Ідея методу Халецького полягає в розкладі квадратної матриці системи Ax = b в добуток двох трикутних матриць.

Представимо матрицю у вигляді добутку двох трикутних матриць

,

де 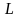є нижньою трикутною матрицею, а 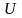є, відповідно, верхньою трикутною матрицею.

Тоді рівняння Ax = b запишеться

.

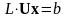Оскільки матриці та є трикутними, розв'язок останнього рівняння зводиться до розв’язування послідовності систем

.

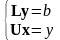Побудова матриці здійснюється за формулами:

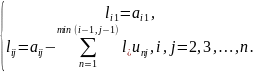
_{А матриці}

Приклад 3. Знайти розв’язок системи Ax = b, де

,

методом Халецького.

Розв’язання. Зобразимо матрицю А у вигляді

Для цього знайдемо коефіцієнти матриць та .

Коефіцієнти першого стовпчика матриці обчислимо за формулами 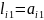. Отримаємо

, , .

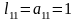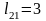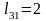Коефіцієнти першого рядка матриці обчислимо за формулами 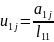. Отримаємо

, , .

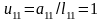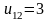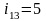Інші коефіцієнти матриці знайдемо за формулою

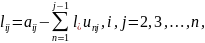
а матриці за формулою

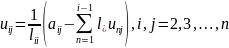
Відповідно будемо мати

,

,

,

,

,

,

.

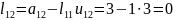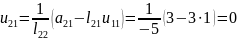
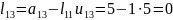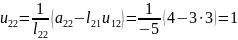
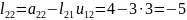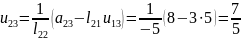
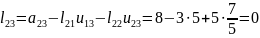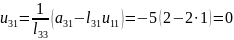
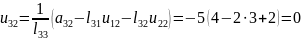
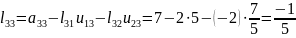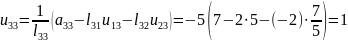Отже,

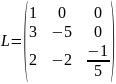та

Маючи трикутні матриці знайдемо розв’язок системи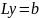 . Отримаємо 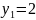, , 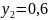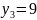та розв’язок системи . Будемо мати , , .
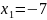
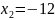
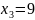