
- •Теория по алгебре
- •6. Матрицы и определители. Прямоугольную таблицу
- •12. Критерий совместимости системы линейных уравнений (теорема Кронекера-Капелли).
- •13. Базис и размерность конечного векторного пространства.
- •14. Евклидовы пространства. Ортонормированные базы.
- •15. Многочлены от одной переменной. Деление многочленов.
- •16. Многочлены от нескольких переменных, симметричные многочлены.
- •17. Многочлены над числовым полем.
- •18. Строение простого алгебраического расширения.
Теория по алгебре
Группы. Примеры групп. Простейшие свойства группы. Подгруппы. Гомоморфизм и изоморфизм групп.
Среди алгебраических систем важнейшую роль играют группы.
Определение: Не пустое множество G с какой-то ассоциативной операцией *, которое является и обратимой называется группой.
Пример: <A, *>
a*(b*c)=(c*a)*b
a*x=b, x*a=b
Однако, проверить
обратимость операции бывает достаточно
сложно, поэтому проверка группы проводится
по следующим правилам: <A,
+>, a,b,c,![]() A
A
a*b
2)
![]() (квантор
существует и он единственный)
(квантор
существует и он единственный)
e A, a*e=e*a=a, e-нейтральный элемент.
Когда e=0, это аддитивная запись, т. к. сложение
Когда e=1 – мультипликативная запись, так как умножение.
3)
![]() Существует симметричный элемент
Существует симметричный элемент
![]() или (-a)
или (-a)
![]() мультипликативная
мультипликативная
![]() аддитивная запись
аддитивная запись
4) (a*b)*c=a*(b*c) свойство ассоциативности
Пример: (множество натуральных чисел с операцией +)-<N,+>
Определение: Группа называется коммутативной, если выполняется свойство коммутативности: a*b=b*a
Пусть множество
G
является группой относительно некоторой
операции. Подмножество H
![]() в котором выполняются свойства 1-4
относительно той же операции называется
подгруппой.
в котором выполняются свойства 1-4
относительно той же операции называется
подгруппой.
То есть, множество H также является группой относительно той же операции звездочка (*).
Из определения следует, что любая группа является своей подгруппой и что любое множество состоящее только из единицы группы так же будет ее подгруппой.
Множество положительных рациональных чисел является группой относительно операции умножения и одновременно является подгруппой мультипликативной группы положительных действительных чисел.
Для того, чтобы установить, что непустое подмножеств H группы G есть подгруппа этой группы достаточно проверить два условия:
a,b H, то a*b H (где звездочка (*) – любая операция), например: ½+½=1/1б т.е Q=1/1
a H, то
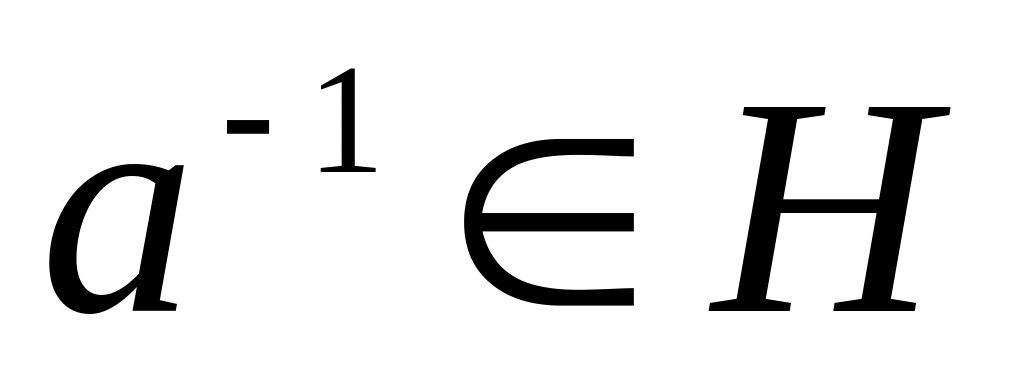 ,
пример: 2/3*3/2=1, где а=2/3 и
,
пример: 2/3*3/2=1, где а=2/3 и
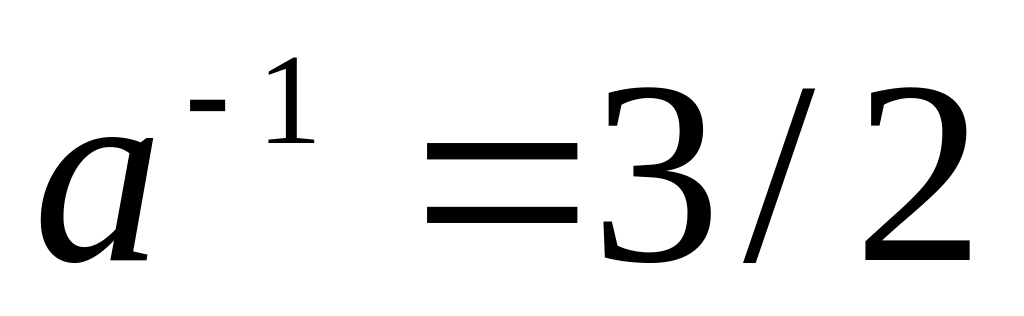
Эти условия можно
заменить одним условием: Для
любых элементов принадлежащих H:
a,b
H,
![]()
![]()
Отображением
группы G
на множество G’(G
штрих) с одной операцией называется
гомоморфизмом
если это отображение сохраняет операцию,
то есть для
любых элементов группы a,b
G
из условия:
![]()
Пример: <N,+> и <R,*>
Пусть даны два множества A и A’ (A штрих)
<A,0>, <A’,*>

<A,0> <A’,*>
Теорема: Гомоморфный образ группы так же является группой относительно своей операции.
При гомоморфизме единицы группы G отображаются в единицы группы G’, а взаимнообратные элементы из G отображаются во взаимообратные элементы G’.
Если гомоморфное отображение взаимооднозначно, то оно называется изоморфным или изоморфизмом.
Изоморфные группы можно считать совпадающими.
2. Кольца. Примеры колец. Простейшие свойства кольца. Подкольца. Гомоморфизм и изоморфизм колец.
Множество действительных чисел R является группой относительно операции сложения, причем эта группа коммутативна, то есть выполняются следующие свойства:
(a+b)+c=b+(c+a) свойство ассоциативности
a+b=b+a свойство коммутативности
a+x=b это уравнение имеет единственное решение.
Кроме того, операция сложения связана с операцией умножения двумя законами дистрибутивности:
a(b+c)=ab+ac
(a+c)b=ba+bc
Операция умножения обладает свойством пять:
a(bc)=(ab)c
Множество K с операцией сложения, умножения называется кольцом, если для любых элементов a,b,c K выполняются свойства 1-5.
Пример: Множество квадратных матриц порядка n является кольцом относительно операции умножения и сложения матриц. Множество целых чисел относительно операции сложения и умножения чисел.
Свойства колец:
Будем использовать аддитивную терминологию (по сложению). Нейтральный элемент равен нулю, а противоположный (-a)
–(-a)=a
a-b=a+(-b)
–a-b=(-a)+(-b)
a-a=0
a(b-c)=ab-ac или (b-c)a=ba-ca
a*0=0 или 0*a=0
(-a)b=-ab, a(-b)=-ab, -a*(-b)=ab
Отличные от нуля элементы a и b? Произведение которых равно 0 называют делителями нуля.
Пример:![]() -эти
матрицы называют делителями нуля.
-эти
матрицы называют делителями нуля.
Подмножество M кольца R называется подкольцом, если оно само является кольцом при тех же операциях сложения т умножения, которые определены в кольце R.
Пример: Кольцо четных целых чисел является подкольцом кольца целых чисел, а кольцо целых чисел является подкольцом кольца рациональных чисел.
Теорема: Для того, чтобы не пустое подмножество M кольца К ,было его подкольцом необходимо и достаточно, чтобы сумма, разность и произведение двух любых из M также принадлежало множеству M (чтобы не выйти за пределы этого множества).
Пусть R1 и R2 произвольные кольца, если R2 является образом кольца R1 то:
Образ нуля R1 кольца при отображении переходит в ноль кольца R2.
Единица из R1 переходит в единицу из R2.
Для всякого элемента a кольца R1 образ элемента противоположного элементу a равен элементу противоположному образу элементу x.
Два кольца R1 и R2 называются изоморфными, если R1-гомоморфна R2, a R2-гомоморфна R1.
 -
гомоморфизм
-
гомоморфизм
 -
изоморфизм
-
изоморфизм
3. Алгебры, алгебраические системы.
Свойства операций состоит в следующем: двум элементам из некоторого множества соответствует некоторый третий элемент.
Картеж - упорядоченный набор из n-элементов.
Операцией над множеством a называется отображение, соответствующее каждому картежу <a1>,<a2>… из A определенный элемент этого же множества.
Операции будем обозначать *, 0 и т.п.
Определение: Всякое множество с заданными в нем операциями будем называть алгебраическими множествами.
Пример: <N,+> и <R,*>
Пусть даны два множества A и A’ (A штрих)
<A,0>, <A’,*>
<A,0> <A’,*>
Отображение системы A на A’ (штрих) сохраняющее операции называется гомоморфизмом, при этом система A’ является гомоморфным образом системы A.
Пример: Множество целых чисел Z с операцией сложения и множество действительных чисел на отрезке [-1;1] с операцией умножения. Эти две системы являются гомоморфными.
Гомоморфное отображение A на систему A’, при котором множество A первой системы отображается на множество A’ второй системы взаимооднозначно называется изоморфизмом.
Пример: Множество действительных чисел с операцией сложения и множество диагональных матриц второго порядка с операцией сложения:
Пример:
A<R,+>; A’<![]() >
>
a,b
![]()
![]()
![]()
Изоморфные алгебраические системы отличаются лишь такими признаками, которые связаны с конкретной природой элементов и операций. Во всем остальном изоморфные системы не различимы - любое утверждение, которое формируется только с помощью равенств связывающих элементы и операции истинно или ложно одновременно для каждой изоморфной системы.
В системе с одной операцией звездочка(*) имеется такой нейтральный элемент, что композиция произвольного элемента a и нейтрального элемента равна элементу a.
Пример: 1. <R,+>,2.
<![]() >,
3. <Q,*>,
4.множество поворотов на угол
>,
3. <Q,*>,
4.множество поворотов на угол
![]() .
.
1. a![]() ,
a+0=a;
,
a+0=a;
2.
![]() ;
3.
;
3.
![]() ;
4.
;
4. -
множество поворотов на 120 градусов, 360
и т.д.
-
множество поворотов на 120 градусов, 360
и т.д.
4. Поле. Примеры полей. Простейшие свойства поля.
Дано множество для произвольных элементов которого выполняются свойства:
a+(b+c)=(a+b)+с ассоциативность
a+b=b+a коммутативность
a+x=b единственное решение
a(b+c)=ab+ac или (b+c)a=ba+ca дистрибутивность
a(bc)=(ab)c
ab=ba
ax=b единственное решение
Множество P с операциями сложения и умножения называется полем, если в P содержатся элементы, отличные от нуля для которых выполняются свойства 1-7.
Поле является кольцом, для которого выполняются дополнительные требования 6-7, поэтому все свойства колец будут справедливы и для полей.
Пример: Множество рациональных чисел с обычными операциями сложения и умножения являются полем, а множество целых чисел относительно обычных операций сложения и умножения не являются, где не выполняется 7 свойство:
2х=7
Х=7/2-не целое число.
Свойства полей:
–(-a)=a
a-b=a+(-b)
–a-b=(-a)+(-b)
a-a=0
a(b-c)=ab-ac или (b-c)a=ba-ca
a*0=0 или 0*a=0
(-a)b=-ab, a(-b)=-ab, -a*(-b)=ab
Специфические свойства полей (нет в кольцах):
Поле не содержит делителя нуля. Если
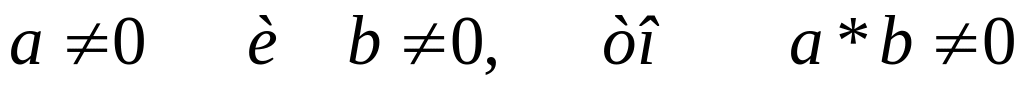
Подмножество не нулевых элементов поля является коммутативной группой относительно операции умножения. Из этого свойства вытекают следствия:
- всякое поле содержит нейтральный элемент относительно операции умножения.
- вместе с каждым не нулевым элементом поле содержит единственный обратный ему элемент.
3. В любом поле выполняются следующие равенства:
а) (-a)=(-1)*a
б) b/a=b*
в)
1/(ab)=![]()
г)
![]()
д)
![]()
5. Числовое поле. Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними. Тригонометрическая форма комплексного числа.
Дано множество для произвольных элементов которого выполняются свойства:
a+(b+c)=(a+b)+с ассоциативность
a+b=b+a коммутативность
a+x=b единственное решение
a(b+c)=ab+ac или (b+c)a=ba+ca дистрибутивность
a(bc)=(ab)c
ab=ba
ax=b единственное решение
Множество P с операциями сложения и умножения называется полем, если в P содержатся элементы, отличные от нуля для которых выполняются свойства 1-7.
Поле является кольцом, для которого выполняются дополнительные требования 6-7, поэтому все свойства колец будут справедливы и для полей.
Замечание:
В поле любой ненулевой элемент обратим, поэтому можно определить операцию деления и частного двух элементов.
![]() ,
где Р – поле.
,
где Р – поле.
Свойства:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Числовые поля:
![]() ,
<Q, +, >
– поле;
,
<Q, +, >
– поле;
![]() ,
R=<R,
+, > - поле;
,
R=<R,
+, > - поле;
![]() , <Q(i),
+ , >
- поле гауссовых чисел;
, <Q(i),
+ , >
- поле гауссовых чисел;
![]() ,
<Q(
,
<Q(![]() ),
+, >
- квадратичное поле.
),
+, >
- квадратичное поле.
Существуют различные способы построения комплексных чисел. Рассмотрим следующий подход, где комплексное число интегрируется как пара действительных чисел.
![]()
1* z1 + z2 = (x1y1)+(x2y2) = (x1 + x2, y1 + y2)
2* z1z2 = (x1y1)(x2y2) = ( x1x2 – y2y1, x1y2 + x2y1)
Теорема: Алгебра С = < Cz{z=(x,
y), x,y
![]() R},
+, > - поле.
R},
+, > - поле.
(x, 0) = x (обозначим действительную часть)
(0, 1) = i (обозначим мнимую единицу)
i2
= (0, 1)(0,
1) = (-1, 0) = -1
![]() i2=
-1/
i2=
-1/
(0, y) = (y, 0)(0,1) = yi (обозначим);
z = (x, y) = (x, 0) + (0, y) = x + iy
z = x + iy
комплексного числа.
Г еометрическое
представление комплексных чисел и
операций над ними.
еометрическое
представление комплексных чисел и
операций над ними.
![]()
![]() - модуль комплексного числа
- модуль комплексного числа
- аргумент комплексного числа;
Z(x,y)
определен с точностью до 2πк, и аргумент
0 не определен.
Геометрическая интерпретация сложения комплексных чисел
Геометрическая интерпретация
Противоположного комплексного
числа

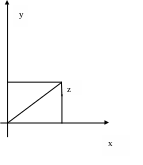 Геометрическая интерпретация сопряженного
комплексного числа
Геометрическая интерпретация сопряженного
комплексного числа
Тригонометрическая форма комплексного числа.
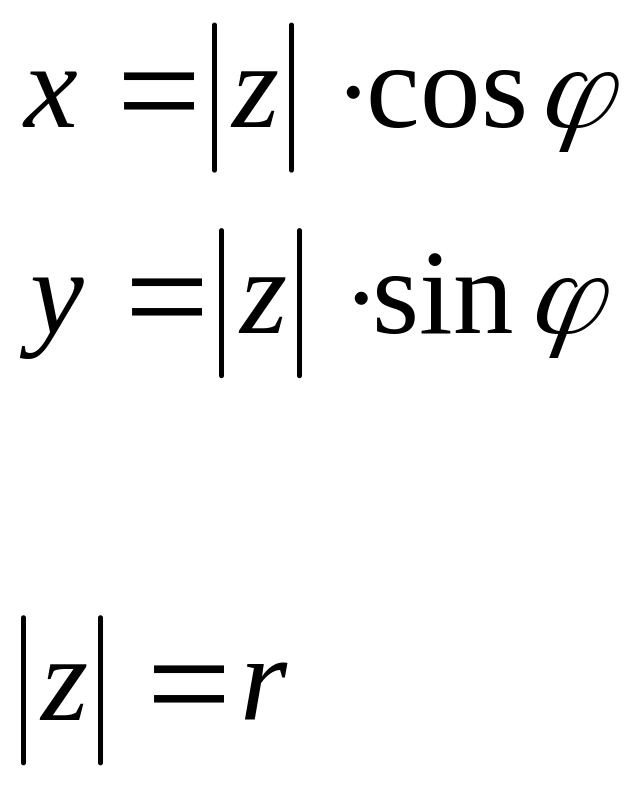
z= x+ iy
=
![]() (
(![]() )
)

z= r( ) тригонометрическая запись комплексного числа
=
![]() (обозначим )
(обозначим )
z = r - показательная форма записи комплексного числа.
Свойства операций над комплексными числами, записанными в тригонометрической форме.
![]()
![]()
![]()
![]()
![]() ,
,
![]()
