
Тема 15 Методы второго порядка
Представление функции вблизи минимума
Матрица ГессеНаправление движения к минимумуМетод Ньютона-Рафсона
Метод интерполяции квадратичной формы
06/25/19 |
1 |
Представление функции вблизи минимума
•Разложим функцию в точке ( x0 , y0 ), находящейся вблизи минимума, в ряд Тейлора :
( x x x0 , y y y0 )
f x, y |
f x0 x, y0 y |
f x0 , y0 |
x |
f x0 , y0 |
y |
f x0 , y0 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
0 |
, y |
0 |
|
|
|
2 |
0 |
, y |
0 |
|
|
|
|
|
2 |
f |
0 |
, y |
0 |
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
2 x y |
|
|
|
|
|
y |
2 |
|
|
|
|
3 |
, y |
3 |
|||||||||||||||||||
2 |
x |
|
|
|
x |
2 |
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
o x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• Пренебрежем x3, y3
06/25/19 |
2 |
f x, y |
F ( x, y) f x0 , y0 |
x |
|
f x0 , y0 |
y |
f x0 , y0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|
x |
|
|
|
|
f x |
|
y |
|
|
|
|
|
|
|
f x |
|
|
|
|
|
||||||
|
1 |
|
|
|
2 |
0 |
, |
y |
0 |
|
|
|
|
|
2 |
0 |
, y |
0 |
|
|
|
|
2 |
0 |
, y |
0 |
|
|
|
|
|
2 |
0 |
, y |
0 |
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
x |
|
|
|
|
|
x2 |
|
|
|
|
x y |
|
|
x y |
|
|
y x |
|
|
|
y x |
|
|
|
y |
|
|
|
y2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
xf |
|
|
|
yf |
|
|
|
1 |
|
2 |
g |
|
x yg |
|
y xg |
|
|
|
y |
2 |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
0 |
|
|
|
x0 |
|
|
|
y0 |
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
21 |
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|||||||||||
• Матрица Гессе |
|
2 f |
2 f |
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
g |
g |
|
|||||
|
x |
x y |
|
||||||||||||
|
G |
|
|
|
|
|
|
|
11 |
|
12 |
||||
|
|
|
2 |
|
|
|
2 |
|
|
g |
g |
|
|
||
|
|
|
f |
|
|
f |
|
22 |
|||||||
|
|
|
|
|
|
|
21 |
|
|
||||||
|
|
y x |
y2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
06/25/19 |
3 |
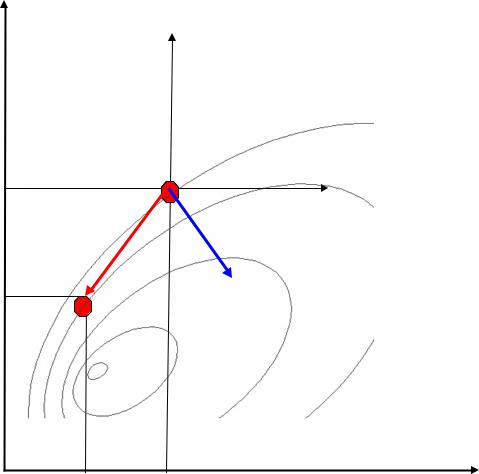
Направление наилучшего спуска
y
y
y0
d* x - F
y*
x* |
x |
x |
|
||
06/25/19 |
0 |
4 |
|
d * ( x* x0 , y* y0 ) (d1*,d2* )
|
|
|
F |
0; |
F |
|
0 |
|
|
|
x |
y |
|
||||||
|
|
|
|
|
|||||
F |
|
f |
x0 |
xg |
yg |
0; |
|||
|
|||||||||
x |
|
|
|
11 |
12 |
|
|||
|
|
|
|
|
|
|
|
||
F |
|
f y0 xg21 yg22 0; |
|||||||
y |
|
||||||||
|
|
|
|
|
|
|
|
||
06/25/19 |
5 |
g |
g |
|
x |
|||
|
11 |
|
12 |
|
||
|
|
|
||||
|
|
g |
|
|
|
|
g |
21 |
22 |
|
y |
||
|
|
|
|
|||
ff
x0
y0
xy
d* g1 g11d2* 21
g12 |
1 |
f |
|
|
|
|
|
|
g22 |
f |
|
|
||
x0
y0
06/25/19 |
6 |
метод Ньютона-Рафсона
1 |
|
0 |
|
g |
g |
1 |
|
f |
|
x |
|
x |
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
11 |
12 |
|
||||
|
0 |
|
|
|
|
|
|||
y1 |
|
y |
|
g21 |
g22 |
|
f |
||
|
|
|
|
|
|
|
|
|
|
x0
y0
06/25/19 |
7 |

В случае n переменных
r0 |
r |
r0 |
rT |
r0 |
|
1 |
rT |
r0 |
r |
o x |
3 |
|
f x |
x |
f x |
x |
f x |
2 |
x |
G x |
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
f |
|
|||
Т f |
f |
, |
, ... |
|
|||||
x |
|
x |
|
||||||
|
x |
|
2 |
|
n |
|
|||
|
1 |
|
|
|
|
||||
|
2 f |
|
|
|
G |
|
|
|
|
|
|
|
||
x x |
|
|
||
|
i |
j |
||
r0 r* r0
G x x f x
06/25/19 |
8 |
Алгоритм Ньютона-Рафсона
r1 r0 1 r0 r0
x x G x f x
•Основной недостаток этого метода заключается в необходимости вычисления матрицы Гессе. Это слишком затратная и некорректная процедура. Поэтому метод Ньютона-Рафсона имеет лишь важное теоретическое значение, как обоснование выбора наилучшего направления спуска.
06/25/19 |
9 |
Анализ поведения функции в окрестности экстремума
• |
|
в точке минимума |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
f x0*, y0* |
|
0; |
f |
x0*, y0* |
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
F ( x, y) f x0 , y0 ( x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
2 |
f x0 |
, y0 |
|
|
2 |
f x0 |
, y0 |
|
|
|
|
2 |
f x0 |
, y0 |
|
|
|
2 |
f x0 |
, y0 |
|
|
|||
|
x2 |
|
x y |
|
y x |
|
y2 |
|
|
||||||||||||||||||||
2 |
|
|
x2 |
|
|
|
x y |
|
|
|
y x |
|
|
|
y2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•квадратичная форма Ф>0, положительно
определена
06/25/19 |
10 |

Квадратичная форма Ф= x2+ y2
|
1 |
0 |
|
Матрица Гессе |
|
|
|
G |
|
|
|
|
0 |
1 |
|
06/25/19 |
11 |

z=- x2- y2 |
1 |
0 |
|
|
|
|
|
||
|
G |
0 |
1 |
|
|
|
|
||
06/25/19 |
12 |

|
|
G |
1 |
1 |
|
|
2 |
2 |
|
|
|
||
z=- x +2* x* y-5* y |
|
|
|
1 |
5 |
|
|
|
|
|
|
||
06/25/19 |
13 |

z=-x2-2*x*y-5*y2 |
1 |
1 |
|
|
|
||
|
G |
5 |
|
|
1 |
|
|
|
|
|
06/25/19 |
14 |

z=x2-2*x*y+5*y2
1 |
1 |
|
G |
5 |
|
1 |
|
|
|
|
|
06/25/19 |
15 |

z=x2+x*y+y2 |
|
1 |
0.5 |
|
G |
|
|
|
|
|
0.5 |
1 |
|
|
06/25/19 |
16 |
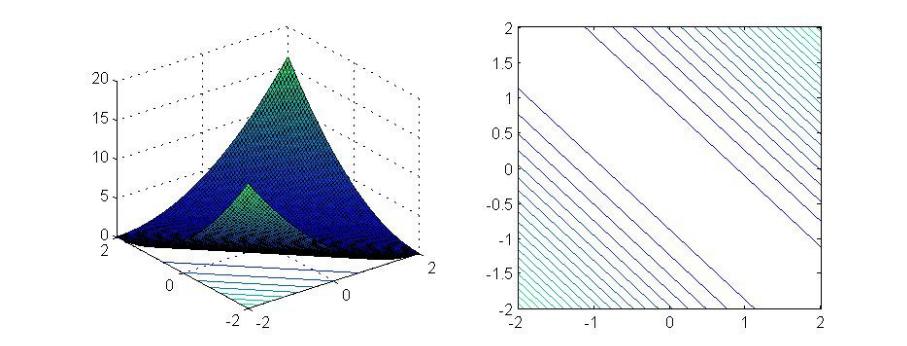
|
1 |
1 |
|
z=x2+2x*y+y2 |
|
|
|
G |
|
|
|
|
1 |
1 |
|
06/25/19 |
17 |

|
1 |
2 |
|
z=x2+4x*y+y2 |
|
|
|
G |
|
|
|
|
2 |
1 |
|
06/25/19 |
18 |
