Тема 18 Методы условной оптимизации2
Понятие функции Лагранжа
Задача линейного программирования
Задача квадратичного программирования
06/25/19 |
1 |
Постановка задач
Найти минимум функции
y f (x1...xn ) f (x).
При ограничениях
gk (x) 0, k 1...m
gk (x) 0, k m 1..m p
06/25/19 |
2 |
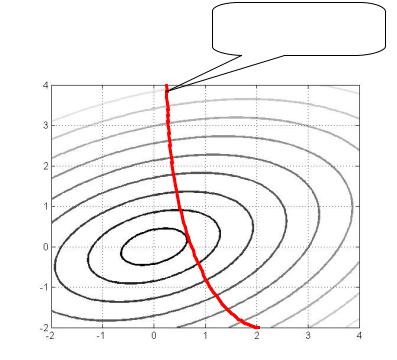
Понятие функции Лагранжа
Вначале на простом примере функции двух переменных рассмотрим какие условия в точке минимума имеют место и как их проще получить
Целевая функция z
Ограничение
g(x, y) 0
Условный минимум лежит
на кривой, описываемой
уравнением g(x, y) ,0
которое неявно определяет
зависимость y=y(x)
f (x, y)
y
g(x,y)=0
x
06/25/19 |
3 |
Получение Условия минимумаВдоль кривой g(x, y) 0
имеет место очевидное соотношение
dg |
|
g |
|
g dy |
|
dy |
|
g |
|
0 |
|
|
|
x |
|||||
dx |
x |
y x |
dx |
g |
|||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
y |
06/25/19 |
4 |
Получение Условия минимума
Запишем условие минимума для функции
z f [x, y]
Вдоль кривой y=y(x)
z f [x, y(x)]
имеем
dz f f dy 0 dx x y x
06/25/19 |
5 |
Условия минимума
Получаем
обозначим
f
xg
x
06/25/19
f |
|
|
|
g |
|
|
|
|
|
|
df x |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|||
x |
y g |
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
|
df |
|
|
|
|
|
|
|
f |
|
|
|
|
Преобразуем |
|
x |
|
y |
0 |
|||
|
|
g |
g |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
y |
|
|
df |
|
|
|
|
y |
|
|
|
g |
– множитель Лагранжа |
|||
|
|
|||
|
y |
|
6 |
Необходимые Условия минимума
Таким образом в точке
минимума f(x,y)
на кривой g(x,y)=0
выполняются
три условия:
f (x*, y*) |
|
dg(x*, y*) |
0 |
|
|
x |
x |
||
|
|
|
||
|
|
dg(x*, y*) |
|
|
f (x*, y*) |
|
|
||
|
|
|
|
0 |
|
y |
y |
||
|
|
|
||
|
|
|
|
|
g(x*, y*) 0
06/25/19 |
7 |
введем функцию Лагранжа
L(x, y, ) f (x, y) g(x, y)
Для нее условия экстремума которые мы выше вывели получаются естественным образом
L |
|
f (x, y) |
dg(x, y) |
0 |
x |
|
x |
x |
|
L |
|
f (x, y) |
dg(x, y) |
0 |
y |
|
y |
y |
|
L |
g(x, y) 0 |
|
||
|
|
|||
|
|
|
|
|
06/25/19 |
8 |
Рассмотрим простой пример
z f (x, y) x2 y2
g(x, y) x y 4 0
Функция Лагранжа |
L(x, y, ) x2 |
y2 (4 x y) |
|
|
Условия экстремума |
L |
2x 0 |
x |
|
|
|
L |
2 y 0 |
|
y |
|
Решение x=2; y=2; =4. |
L |
4 x y 0 |
|
06/25/19 |
9 |
анализ, вблизи точки экстремума
• точка экстремума функции Лагранжа представляет
седловую точку, в которой достигается минимум по переменным xy и максимум по переменной
|
x |
|
|
|
x |
Сечение функции Лагранжа |
|
|
|
при y=2 |
L(x, y, |
) x2 y2 (4 |
x y) |
|
|||
06/25/19 |
|
|
10 |