Презентации и конспект лекции Синицын / Презентации_ВЭиМОвТС / МетодыОптимизации / Лекция1_Классификация_многомерных и_ одномерные

Раздел II. Методы оптимизации

Тема1.

Основные понятия и классификация методов многомерной оптимизации

Постановка задачи Рельеф функции

Классификация методов многомерной оптимизации

Методы нахождения минимума функции одной переменной

Задачи

Главной целью большинства выполняемых на компьютере расчетов является принятие оптимального в конкретной ситуации решения или, что тоже самое, сделать наилучший выбор из множества допустимых вариантов:

сколько и куда вложить денег, чтобы получить наибольшую прибыль

по какой дороге поехать, чтобы сэкономить бензин, время и при этом обеспечить безопасность

как выбрать параметры прибора, что бы при его минимальной стоимости изготовления достигался максимум КПД.

Модели задач выбора

В каждом случае при решении задачи выбора требуется построить математическую модель, описывающую конкретную ситуацию

Формулировка модели содержит некоторое

количество параметров

x x1 , ..., xn

значение которых определяет конкретный вариант

Ценность каждого варианта определяется числом, которое называется критерием.

Если удается сопоставить каждому варианту определенное значение критерия то получаем

целевую функцию

f ( x ) f ( x1 , ... x n )

•В результате, задача принятия оптимального решения приводит к нахождению оптимального (максимального

или минимального) значения f ( x )

• Следует отметить, что нахождение максимума f ( x )

• эквивалентно нахождению минимума f ( x )

• поэтому стандартные программы разрабатываются,

•если существует некоторая -окрестность точки x * , в которой выполняется

•Будем полагать, что f ( x ) непрерывная дважды дифференцируемая функция.

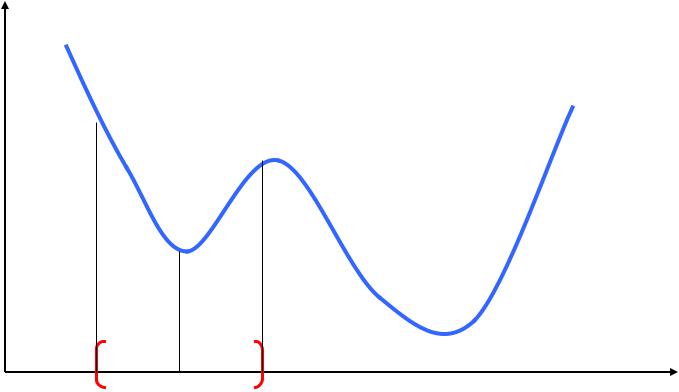
Локальный минимум

f

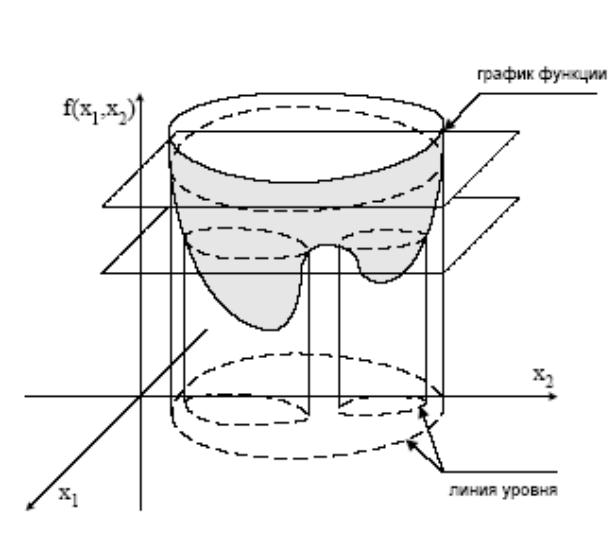
Рельеф функции f ( x1 , x 2 )

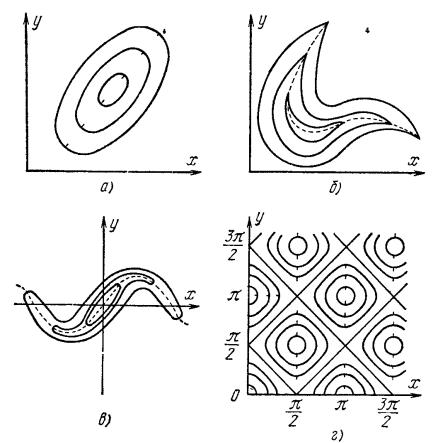
Типы рельефов

котлованный (а)

овражный (б.в),

неупорядоченный (г)