
Презентации и конспект лекции Синицын / Презентации_ВЭиМОвТС / МетодыОптимизации / Лекция3 Методы первого порядка
.pdf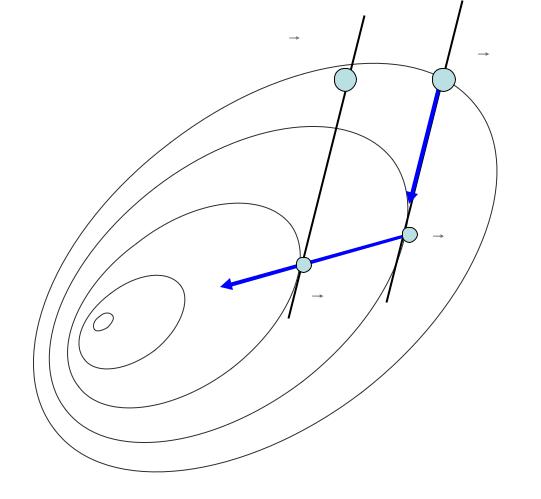
Метод параллельных прямых
В заданной точке х0 выбираем произвольный вектор d1 и делаем спуск в точку х1
Вблизи точки х0 выбираем точку х01
Из нее также делаем спуск в направлении d1 до точки
х11
Вектор d2 проведенный через точки х1 х11 является сопряженным к d1
x 0 1 |
x 0 |
d1
d |
2 |
x 1 |
|
|
x 1 1
05.01.2011 |
21 |

Метод Флетчера-Ривса
g 0 f ( x 0 )
d 1 g1 |
d 0 |
|
d 0 g 0 |
|||
|
g12 |
|
|
|
||
|
|
|
|
|||
g 02 |
d |
1 |
g f ( x 1 ) |
|||
|
||||||
|
|
|
1 |
|||
|
|
|
|
|
||
05.01.2011 |
22 |

Алгоритм метода Флетчера-Ривса
1. |
Задается начальная точка x 0 |
и начальный шаг h |
|
|
|||||||||||||||
|
одномерного спуска , вычисляется. g |
0 |
f ( x |
0 |
) |
d g |
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Повторяем n раз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
Делаем спуск zm |
m in |
f ( x 0 z d ) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Переходим в новую точку |
x |
0 |
x |
0 |
z |
m |
d |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
Вычисляем |
g1 |
f ( x 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. |
Выбирается направление |
|
|
|
|
|
|
|
g |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
d |
g |
|
|
|
|
1 |
d |
|
|
|
|||
|
|
|
|
|
|
1 |
|
g 02 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
6. |
Пересылаем |
g 0 |
g 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Конец повтора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
05.01.2011 |
Если zm< повторим с п.1 |
|
|
|
|
|
|
|
|
|
23 |
||||||||
Конец
05.01.2011 |
24 |
