Розрахунки детермінант матриць:

∆₁₄=(-g₁-jwC₁)(-jwC₂)(K₀g_вих)-(-g₁)( -g₁-jwC₁)(jwC₂+g_вих)=

-jwC₁(g₂g_вих)+jwC₂(g₁K₀*g_вих-g₁g₂)+jwC₁jwC₂(K₀*g_вих-g₂)-g₁g₂g_вих

A(w)=-3*10^-6-5.99999*10^-21*w²

B(w)=jw*5.99995*10^-11

∆₁₁₌(g₁+g₂+jwC₁+g_вх)( jwC₂+g_вих)( g₂+g₃+jwC₂)+(-g₂)(-jwC₂)(K₀*g_вих)-

-(-g₂)(-g₂)(jwC₂+g_вих) -(g₁+g₂+jwC₁+g_вх)(-jwC₂)(-jwC₂)=

g_вих(g₁g₂+ g₁g₃+ g₂g₃+g₂g_вх+g₃g_вх)+

+jwC₁(g₂g_вих+g₃g_вих)+

+jwC₂(g₁g_вих+g₂g₃+g₂g_вих+g₂g_вх+g₃g_вх+g_вхg_вих+g₂K₀g_вих)+

+jwC₁jwC₂ (g₂+g₃+g_вих)

C(w)=3.30399*10^-6-3.11*10^-25*w²

D(w)=jw*6,03361*10^-10

Таким чином комплексний коефіцієнт передавання фільтра, який досліджується, приведений до канонічної форми запису :

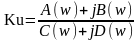
2.2.Розрахунок частотних характеристик фільтра Частотні характеристики досліджуваного фільтра будемо визначати за формулами :

• модуль коефіцієнта передавання (1):

• аргумент коефіцієнта передавання(2):

Результати розрахунків модуля й аргументу частотного коефіцієнта передавання досліджуваного фільтра зведемо в табл.1.1, а також побудуємо графіки АЧХ, ФЧХ та годограф:

Частотні характеристики коефіцієнта передавання досліджуваного фільтра

Рис.2.2 Частотні характеристики досліджуваного активного фільтра :

а) - амплітудно-частотна характеристика (АЧХ).

_б) - фазо-частотна характеристика(ФЧХ)

_{Також побудуємо годограф рис.2.3 (залежність АЧХ від ФЧХ) на діапазоні частот}

ω =10⁹… 10¹⁵ рад/c

_{На рисунку спостерігається рух годографа проти годинникової стрілки. Дане явище зумовлено особливостями заданої схеми, а саме наявністю прямого зв’язку при включенні операційного підсилювача в схему.}

3.Дослідження періодичного сигналу на вході та виході активного фільтра

3.1 Розрахунковий вираз вхідного сигналу активного фільтра

Сума складових вхідного сигналу запишеться у вигляді :

U_вх(t)=U_m1 ∙cos(ω₀t+ ϕ₁)+ U_m2 ∙cos (2ω₀t+ϕ₂)+U_m3∙cos(3ω₀t+ϕ₃)

або з числовими параметрами, попередньо підставивши замість

ω₀=2∙π∙f₀= 1.256*10⁴ рад/c

U_вх(t)=60*10^-3 *cos(1.256*10⁴ *t+0,33333*π)+25*10^-3 *cos(2*1.256*10⁴*t-0,5*π) +

+10*10^-3 *cos(3*1.256*10^4*t+0,5*π); Також обчислимо крок зміни часу,як функцію від періода . Останній дорівнює:

T₀=1/f₀=5*10^-4мкс Крок зміни часу вибираєм рівним: ∆T=0.05∙T₀=2,5*10^-5 мкс

Розрахунки кожної складової та їхньої суми подані в таблиці 3.1:

Таблиця 3.1

На підставі розрахунків будуємо часову залежність вхідного сигналу та його гармонічних складових (рис.3.1, 3.2).

Рис . 3.1 Часова залежність гармонічних складових вхідного сигналу

Рис . 3.2 Часова залежність вхідного сигналу

3.2. Розрахунок гармонічного сигналу на виході досліджуваного аф Щоб знайти вихідний сигнал ми розраховуємо амплітуди та початкові фази гармонік:

_{Після цього знайдені амплітуди і початкові фази гармонік ми підставляємо відповідно у формулу і розраховуємо миттєві значення вихідного сигналу для окремих гармонік:}

та розраховуємо миттєві значення вихідного сигналу як суму миттєвих значень окремих гармонік для моментів часу,які відстають один від одного на 0.05∙T₀:

Таблиця 3.2 Результати розрахунків вихідного сигналу та його гармонік

На підставі розрахунків будуємо часову залежність вихідного сигналу та його гармонічних складових:

Часова залежність вихідного сигналу та його гармонічних складових

Часова залежність вихідного сигналу та його гармонічних складових