36. Стретагическое планирование экспериментов с моделью.

При испытании трудоемких моделей требуется планирование эксперимента. Цель планирования эксперимента – получить максимум полезной информации при минимальных затратах на проведение моделирования.

Затраты (временные) на моделирование зависят

- от числа испытаний на одном эксперименте (n)

- от количества экспериментов (r)

- от кол-ва прогонов (k) если система не стационарна.

При планировании экспериментов:

1. В системе выдляют факторы

2. Факторы анализируют и разделяют на первичные и вторичные

3. Факторы могут быть количественные и качественные. Для первичных факторов определяют уровни или ранги, если фактор качественный. Само планирование экспериментов сводиться к выбору уровней, рангов и их комбинаций.

Говорят о тактическом и стратегическом планировании:

Тактическое – вон с пляжа!

Стратегическое планирование – занимается тем, как уменьшить кол-во экспериментов(r). Можно выделить два крайних плана эксперимента:

1. Однофакторный

2. Полнофакторный

Пример: модель включает 2 параметра

Два стркутурных элемента которые задаются одним параметром

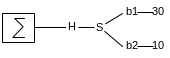
Однофакторный план: в каждом эксперименте меняется только один параметр – 40 экспериментов.

Полнофакторный план – 300 экспериментов. Остальные варианты лежат между этими полюсами.

Частично плановые факторы:

Рандомизированный план – случайным образом берутся b₁ и b₂.

Дробный факторный план – для каждого эксперимента берутся min и max.

38. Оценка результатов имитационного моделирования

Пусть - реальное значение оцениваемой характеристики. В результате статистического эксперимента мы можем получить значений СВ. - оценка

величины .

М ежду реальным значением и оценкой всегда существует погрешность.

Оценке СВ можно доверять с некоторой вероятностью

- доверительная вероятность

Чаще всего при моделировании всегда в качестве оценок вычисляются и .

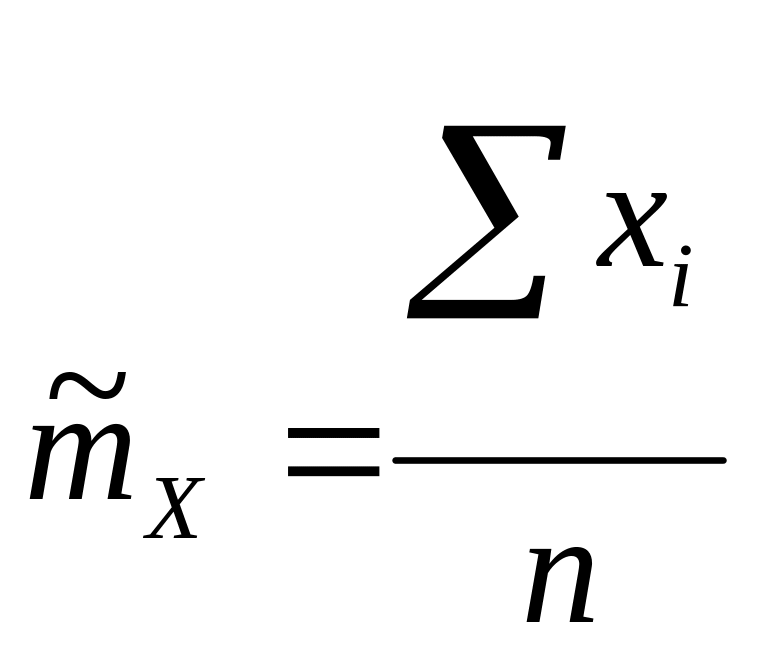
Эти оценки являются СВ, т.е. мало их вычислить, но нужно указать доверительный интервал. Пусть - СВ распределённая по нормальному закону. и - константы.

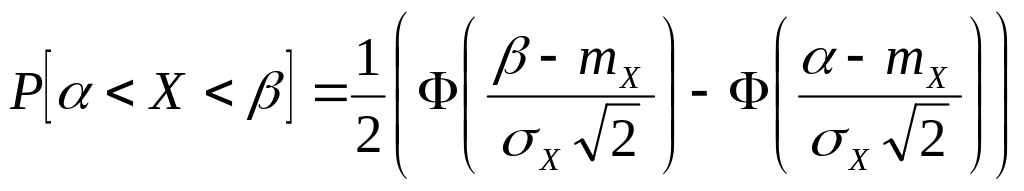В силу центральной предельной теоремы при , закон распределения и становится нормальным. На практике это происходит при слагаемых. Это значит, что можно воспользоваться формулой и получим:

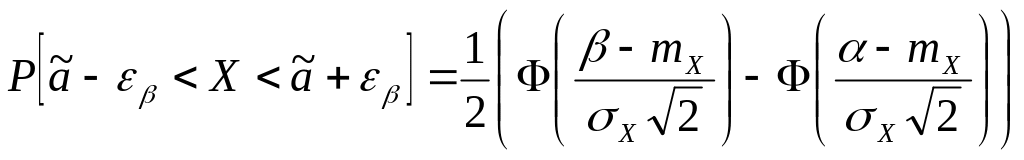
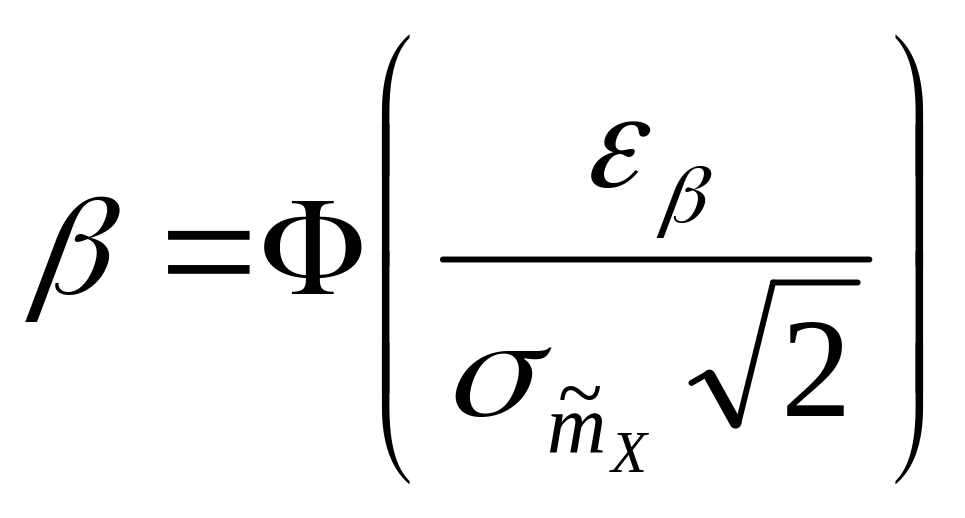т.е. доверительная вероятность вычисляется по функции Лапласа. Чаще всего в инженерной практике поступают наоборот. Сначала задаются , а затем находят и строят доверительный интервал.

Обычно

Для дисперсии процедура аналогична, но все средние изменяются на оценку дисперсии.

39. Общая характеристика метода Монте-Карло.

Метод Монте-Карло основан на замене исходного объекта независимо от его природы случайными процессами, чьи характеристики (например, m_x,D_x) совпадают с характеристиками объекта. Метод используется как для моделиро­вания вероятностных так и детерминированных объектов (например, для реше­ния моделей, описанных дифференциальными уравнениями в частных произ­водных или n-кратными интегралами). Широко применяется для генерации случайных объектов (событий, процессов) с заданными вероятностными харак­теристиками, необходимых для организации имитационного моделирования.

Достоинства метода: - инвариантность к объекту исследования, однотип­ность схемы организации моделирования и соответственно универсальность применения; - сравнительно низкая трудоёмкость, так как сами вычисления, как правило, однотипны и относительно несложны, а их объёмы зависят от точнос­ти почти линейно.

Общая схема применения метода включает: подбор и замену объекта аде­кватной вероятностной схемой (моделью), характеристики которой совпадают с вычисляемыми характеристиками объекта; выполнение вычислений по схеме необходимое количество раз и накопление статистических данных; выполне­ние статистической обработки результатов и их оценки

40. Пример использования метода Монте-Карло.

Пример 1 Объект – нерегулируемый перекресток, событие – одновременное появление транспортных средств с пересекающимися маршрутами.

Пусть известен закон распределения времени появления трансп. средства по каждой из пересекающихся улиц: f_τ и f_t. Тогда при моделировании мы заменяем объект двумя случ. процессами: поток с распределением f_τ и поток с распределением f_t.

В – обрабатывает t_i и τ_i. Если t_i = τ_i, то в С – счетчик событий добавляется 1, если они не совпадают, то миним. значение отбрасывается и берется следующее значение от этого же генератора. Процедура повторяется нужное кол-во раз.

После завершения эксперимента накопленное в счетчике значение делится на кол-во экспериментов k/n – это и есть вероятность события.

Пример 2 смоделировать работу спецвычислителя.

Вычислитель включает:

- накапливающий сумматор

- устр-во управления

- регистры и т.д.

Имеет реальную структуру и реальный алгоритм управления. Известно, что вх. значения явл. случ. величинами, они принадлежат одной генеральной совокупности и обладают плотностью f_x. Вых. значения – случ. величины с плотн. распр. f_y. Требуется промоделировать работу устройства и оценить выходные значения.

Если проводится имитационное моделирование то мы должны в модели отобразить структуру вычислителя. Промоделируем объект используя метод Монте-Карло.

Пример 3. Детерминированный объект - интеграл от некоторой функции.

Чтобы промоделировать наш объект - - надо вычислить площадь под графиком функции. Для удобства промасштабируем ф-ю таким образом, чтобы она вписалась в единичный квадрат. Будем случ. образом в квадрат набрасывать точки – обе координаты случ. точки подчиняются равномерному закону.

Повторим эксперимент n раз.

0≤k≤n – сколько точек попало в заштрихованную область.

t=k/n – P(Z), Z – точка попала в заштрихованную область.

Вычислить интеграл в данном случае равносильно вычислению вероятности события Z.

Детерминированный объект мы заменяем случ. событием – это и будет модель Монте-Карло для нашего объекта.

Указанная схема должна быть выполнена n раз, после чего обрабатываем статистику