2.5 Булеан

Множество всех подмножеств множества М называется булеаном и обозначает­ся 2^М:

2^М = {А| АМ}

Теорема.Для конечного множества М |2^М| = 2^|M|

Доказательство:

Индукция по |M|. База: если |M| = 0, то М= Ø и 2^Ø = {Ø}. Следовательно,

|2^Ø | = |{Ø}| = 1 = 2⁰=2^|Ø|.

Индукционный переход: пусть M |М| <k→|2^М| = 2^|M|. Рассмотрим М = {а₁,... ,a_k},

|М| = k. Положим

M₁ = {X 2^M |a_kϵX} иМ₂ = {X2^м | a_kX}.

Имеем 2^M = M₁UМ₂ и Mi∩М₂ = Ø. По индукционному предположению |M₁| = 2^k-1,

|M₂| = 2^k-1. Следовательно, |2^М| = |M₁| + |M₂| =2^k-1 + 2^k-1=2×2^k-1 =2^k=2^М.

Пример. Пусть X = {1,2,3}. Тогда множество всех подмножеств X будет

2^X = {0, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, X}.

Глава 3. Упорядоченные множества

3.1 Кортеж

Пусть А и В — произвольные множества. Упорядоченная пара на множествах А и В, обозначаемая записью <a,b>, определяется не только самими элементами аА и bВ, но и порядком, в котором они записаны. И в этом состоит ее существенное отличие от неупорядоченной пары. Если А = B, то говорят об упорядоченной паре на множестве А.

Две упорядоченные пары <a,b>и <c, d>на множествах А и В называют равными, если а = c и b = d.

Упорядоченную пару <a,b>не следует связывать с множеством {а, b}, так как упорядоченная пара характеризуется не только составом, но и порядком элементов в ней. Более того, определение этого объекта вообще не позволяет рассматривать его как множество. Но упорядоченную пару можно определить и как множество, полагая, что упорядоченная пара <а,b> есть неупорядоченная пара {{а}, {а, b}}, включающая в себя одноэлементное множество {а} и неупорядоченную пару {а, b}. При а = b получаем <a,a>= {{а}}. Такое определение не изменит сути понятия, но тогда следует не определять явно равенство упорядоченных пар, а доказывать теорему о равенстве упорядоченных пар как определенного вида множеств.

Обобщением понятия упорядоченной пары является упорядоченный n-набор, или кортеж. В отличие от конечного множества {a₁,...,a_n} кортеж <a₁, ..., а_n> на множествах А₁, ..., А_n характеризуется не только входящими в него элементами a₁А₁, ..., а_nА_n, но и порядком, в котором они перечисляются.

Два кортежа α=<a₁, ..., а_n>и β=<b₁, ..., b_n>на множествах А₁, ..., А_n равны, если a_i=b_i, i=.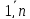

Число n называется длиной кортежа (или размерностью кортежа), а элемент а_i — i-й проекцией (компонентой) кортежа. Для двух кортежей одинаковой размерности их компоненты с одинаковыми номерами называют одноименными компонентами. Определение равенства кортежей можно переформулировать так: два кортежа одинаковой размерности равны тогда и только тогда, когда их одноименные компоненты совпадают. В отличие от множества, кортеж может иметь повторяющиеся элементы, но все эти элементы различны. Компоненты кортежа могут обозначать любые понятия, объекты, в том числе элементы множества или кортежа.

Простейшим примером кортежа является арифметический вектор.

Кортеж, который не содержит компонентов в своем составе, называется пустым кортежем и обозначается α=<>. Длина этого кортежа равна нулю.

Для любых кортежей α, β, γ справедливы утверждения:

• Если α=β, то β=α

• Если α=β и β = γ, то α= γ