
- •Министерство образования и науки Украины
- •4.1 Компьютерное моделирование динамических звеньев (Раздел 1)
- •4.1.2. Сравнение переходных характеристик различных звеньев
- •4.1.3. Проведение компьютерных экспериментов для получения частотных характеристик отдельных звеньев и их сравнение
- •4.2. Компьютерное моделирование соединений динамических звеньев (Раздел 2)
- •4.3. Моделирование сложных динамических систем (Раздел 3)
- •Раздел 4. Компьютерное моделирование стохастических процессов с заданными свойствами
- •4.1 Постановка задачи на моделирование стохастического процесса заданными свойствами
- •4.2 Расчет формирующего фильтра для моделирования стохастического процесса с заданными свойствами
- •4.3 Моделирование стохастического процесса и оценки его характеристик
- •Раздел 5. Моделирование сложных динамических систем с стохастическими входными воздействиями.
Министерство образования и науки Украины
ОДЕССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ ПИЩЕВЫХ ТЕХНОЛОГИЙ
Кафедра автоматизации
Производственных процессов
КУРСОВА РАБОТА
по дисциплине
«Основы компьютерного моделирования технических систем»
Тема курсово работи:
«КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
ТЕХНИЧЕСКИХ СИСТЕМ»
Студент: Синянский М.А. Преподаватель: Лагерная С.И.
Факультет: АЕКС та УП Курс: II
Группа: А – 20(а)
Одесса 2013
Введение
Цель курсовой работы - научиться компьютерному моделированию динамических звеньев и систем с детерминированными входными воздействиями и стохастическими воздействиями с заданными свойствами.
Задача курсовой работы - получение студентами практических навыков в проведении компьютерных экспериментов по получению переходных, частотных характеристик динамических звеньев и систем, а также проведения моделирования стохастических процессов с заданными свойствами и нахождении реакции динамических систем на них.
Работа над курсовым проектом, безусловно, начинается с выбора варианта. Мой вариант № 17, согласно ему я выбираю исходные данные для выбора варианта задачи:
Вибор варианта |
Расчёт параметров ПФ |
Передаточные функции динамических звеньев с расщитаными параметрами |
n=0 |
|
|
m=2 |
|
|
I=1 |
|
|
J=2 |
|
|
g=2 |
|
|
a=0.6 |
|
|
b=0.7 |
|
|
c=0.1 |
|
|

Рис.1 Структурная схема динамичной системы
4.1 Компьютерное моделирование динамических звеньев (Раздел 1)
4.1.1. Проведение компьютерных экспериментов с получением переходных характеристик отдельных звеньев.
Задание. Получить при помощи моделирования переходные характеристики всех динамических звеньев, которые входят в схему сложной динамической системи, изображенной на рис.1
Собираем схему для проведения эксперимента с получением переходной характеристики звена чистого запаздывания с передаточной функцией = .
Используем блок из библиотеки Nonlinear – «Transport Delay». В настройках блока устанавливаем параметры звена – час запаздывания (Time Delay),который равен 0,48 с.
 Согласно
с рекомендациями устанавливаем в меню
Simulation / Parameters шаг моделирования, который
равен 1/10 от времени запаздывания
- 0,048 с. Время моделирования
1 с.
Согласно
с рекомендациями устанавливаем в меню
Simulation / Parameters шаг моделирования, который
равен 1/10 от времени запаздывания
- 0,048 с. Время моделирования
1 с.

Рисунок 2 Схема моделирования для получения переходной характеристики звена чистого запаздывания
Рисунок 3 Окно настройки параметров моделирования
Запускаем процедуру расчета модели. После окончания расчета открываем блок ―ScopeNew‖, в котором видим переходную характеристику звена.


Рисунок
2
Переходная характеристика звена чистого
запаздывания с передаточной функцией
=
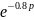 .
.
а) шаг моделирования 0,48с б) шаг моделирования 0,048с

 Соберем
схему для получения переходной
характеристики звена с передаточной
функцией
=
. Это
дифференцирующее
реальное звено 1 порядка. Используем
блок библиотеки Linear – «Transfer Fcn».
Устанавливаем шаг моделирования
0,12/3=0,04
, время моделирования
5*0,12=0.6
Соберем
схему для получения переходной
характеристики звена с передаточной
функцией
=
. Это
дифференцирующее
реальное звено 1 порядка. Используем
блок библиотеки Linear – «Transfer Fcn».
Устанавливаем шаг моделирования
0,12/3=0,04
, время моделирования
5*0,12=0.6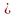 1
с.
1
с.
 Рисунок
5
Схема
моделирования для получения переходной
характеристики звена
Рисунок
5
Схема
моделирования для получения переходной
характеристики звена
Рисунок 6 Окно настройки параметров моделирования
Рисунок 7 Переходная характеристика звена
Рисунок
6 Окно настройки параметров
моделирования

 Используем
блок библиотеки Linear
– «Transfer
Fcn».
Устанавливаем
шаг моделирования 0,3/3=0,1
, время моделирования
0,3*5=1,5 с.
Используем
блок библиотеки Linear
– «Transfer
Fcn».
Устанавливаем
шаг моделирования 0,3/3=0,1
, время моделирования
0,3*5=1,5 с.
 Рисунок
8
Схема моделирования для получения
переходной характеристики звена
Рисунок
8
Схема моделирования для получения
переходной характеристики звена
Рисунок 10 Переходная характеристика звена Рисунок 9 Окно настройки параметров моделирования

 Соберем
схему для получения переходной
характеристики звена с передаточной
функцией
=
-
статическое
апериодическое звено 1 порядка.. Используем
блок библиотеки Linear
– «Transfer
Fcn».
Устанавливаем
шаг моделирования
1.2/3=0,4 , время моделирования
1.2*5=6 с.
Соберем
схему для получения переходной
характеристики звена с передаточной
функцией
=
-
статическое
апериодическое звено 1 порядка.. Используем
блок библиотеки Linear
– «Transfer
Fcn».
Устанавливаем
шаг моделирования
1.2/3=0,4 , время моделирования
1.2*5=6 с.
 Рисунок
11
Схема моделирования для получения
переходной характеристики звена
Рисунок
11
Схема моделирования для получения
переходной характеристики звена
Рисунок 12 Окно настройки параметров моделирования
Рисунок 13 Переходная характеристика звена

 Соберем
схему для получения переходной
характеристики звена с передаточной
функцией
=
-
астатическое
(интегрирующее) звено 1 порядка.
Используем блок библиотеки Linear
– «Transfer
Fcn».
Устанавливаем
шаг моделирования
1.8/3=0,6 , время моделирования
1.8*5=9 с.
Соберем
схему для получения переходной
характеристики звена с передаточной
функцией
=
-
астатическое
(интегрирующее) звено 1 порядка.
Используем блок библиотеки Linear
– «Transfer
Fcn».
Устанавливаем
шаг моделирования
1.8/3=0,6 , время моделирования
1.8*5=9 с.
 Рисунок
14
Схема моделирования для получения
переходной характеристики звена
Рисунок
14
Схема моделирования для получения
переходной характеристики звена
Рисунок 3 Переходная характеристика звена Рисунок 15 Окно настройки параметров моделирования
Соберем схему для получения переходной характеристики звена с передаточной функцией =0.5 – статичное без инерционное звено. Используем блок библиотеки Linear – «Gain». Устанавливаем шаг моделирования 0.01 и время моделирования 5 с.


 Рисунок
17 Схема
моделирования для получения переходной
характеристики звена
Рисунок
17 Схема
моделирования для получения переходной
характеристики звена
Рисунок 19 Переходная характеристика звена
Рисунок 4 Окно настройки параметров моделирования
Соберем схему для получения переходной характеристики звена с передаточной функцией =1 – статичное без инерционное звено. Используем блок библиотеки Linear – «Gain». Устанавливаем шаг моделирования 0.01 и время моделирования 5 с.

 Рисунок
20 Схема
моделирования для получения переходной
характеристики звена
Рисунок
20 Схема
моделирования для получения переходной
характеристики звена
Рисунок 22 Переходная характеристика звена
Рисунок 21 Окно настройки параметров моделирования

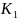 =0.5
=0.5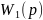 =0.5
- статическое
безинерционное звено
=0.5
- статическое
безинерционное звено
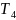 =a=0.6
=a=0.6 =1
- статическое
безинерционное звено
=1
- статическое
безинерционное звено =0.8*0.6=0.48
=0.8*0.6=0.48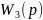 =0
- статическое
безинерционное звено
=0
- статическое
безинерционное звено =1.2
=1.2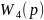 =
=
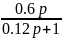 –дифференцирующее
реальное звено 1 порядка
–дифференцирующее
реальное звено 1 порядка =0.5*0.6=0.3
=0.5*0.6=0.3 =
=
 – звено чистого запаздывания
– звено чистого запаздывания
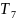 =2*0.6=1.2
=2*0.6=1.2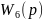 =
=
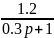 -статическое
апериодическое инерционное звено 1
пор.
-статическое
апериодическое инерционное звено 1
пор.
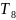 =a=0.6
=a=0.6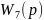 =
=
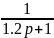 -
статическое
апериодическое инерционное звено 1
пор.
-
статическое
апериодическое инерционное звено 1
пор.
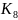 =2
=2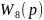 =
=
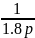 астатическое
(интегрирующее) звено 1 порядка
астатическое
(интегрирующее) звено 1 порядка