Таврический национальный университет

им. В.И. ВЕРНАДСКОГО

кафедра геометрии

Методические указания

для практических занятий по курсу

«Высшая математика»

Раздел IV: Интегральное исчисление

для студентов I курса дневной и заочной форм обучения специальностей:

• 6.070400 – биология,

• 6.070500 – география,

• 6.070800 – экология и охрана окружающей среды

образовательно-квалификационного уровня «бакалавр»

Симферополь 2003

Печатается по решению научно ­– методического совета Таврического национального университета от

Неопределённый интеграл

Функция называется первообразной функцией для данной функции на данном промежутке, если на этом промежутке .

Неопределённым интегралом функции от называется совокупность всех функций , производная которых равна . Неопределённый интеграл обозначается символом . Можно записать:

,

где – подынтегральное выражение,

– подынтегральная функция,

– произвольная постоянная.

Интегрирование – действие, обратное дифференцированию, поэтому оно проверяется нахождением производной:

Основные свойства неопределённого интеграла

Таблица основных неопределённых интегралов

Таблица производных	Таблица неопределённых интегралов	№
		(1)
		(2)
		(3)
		(4)
		(5)
		(6)
		(7)
		(8)
		(9)
		(10)
		(11)
		(12)
		(13)
		(14)

§1. Нахождение табличных интегралов (интегрирование по формулам)

Пример 1. Найти .

Решение. Это интеграл от алгебраической суммы. Применяя сначала свойства 2 и 3, а затем формулу (3) табличных интегралов, получим:

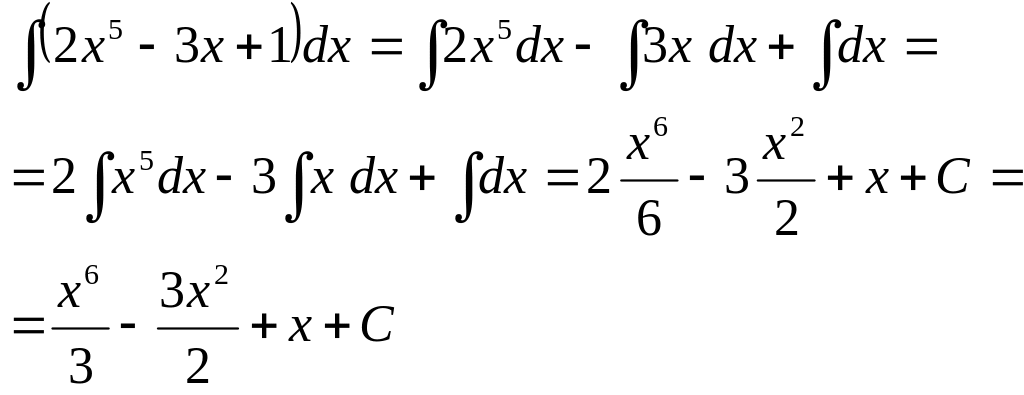
Пример 2. Найти .

Решение. Применим формулу сокращённого умножения (квадрата суммы) и свойства 2 и 3:

Пример 3. Найти .

Решение. Воспользуемся формулой: :

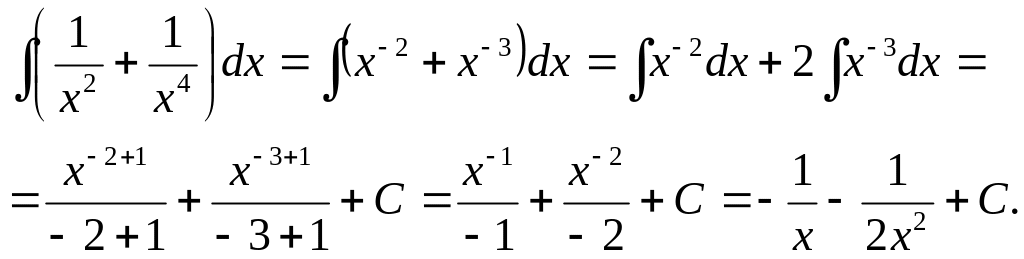
Пример 4. Найти .

Решение. Представим данный интеграл в виде суммы двух интегралов; для этого каждое слагаемое числителя делим на знаменатель подынтегральной функции:

Пример 5. Найти .

Решение. Воспользуемся формулой перехода к дробному показателю: :

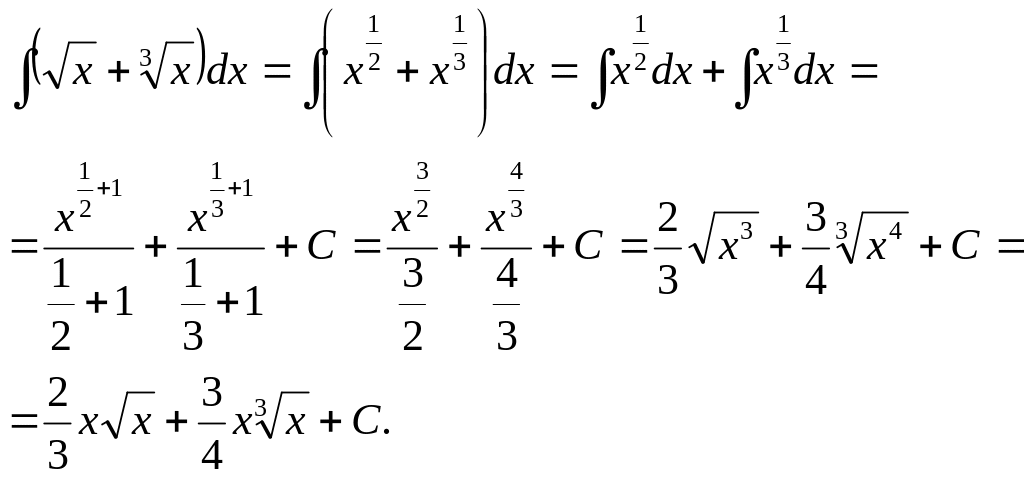
Пример 6.

Пример 7.

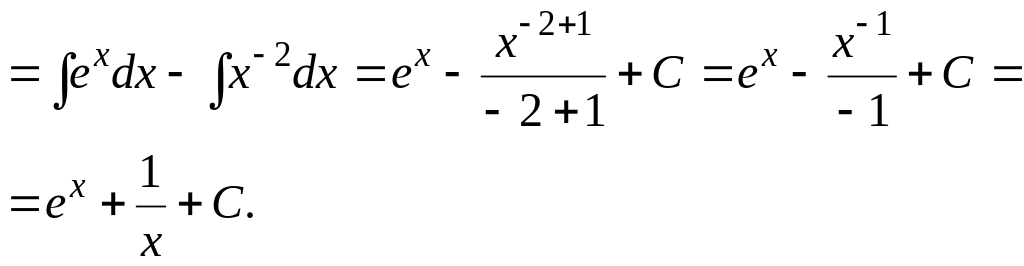
Пример 8. Найти .

Решение. Перепишем интеграл в виде:

числитель подынтегральной функции, то есть единицу, запишем в виде тригонометрического тождества: . Таким образом,

Пример 9.

Используем формулы понижения степени и двойного угла:

Получим:

Пример 10. Найти .

Решение. В числителе подынтегральной функции осуществим следующее тождественное преобразование: прибавим и отнимем единицу; затем разложим интеграл на сумму 2-х интегралов:

К числителю первого интеграла применим формулу разности квадратов, а второй вычислим по формуле (13):

Пример 11. Найти интеграл

Решение. Запишем числитель в виде

почленно разделим числитель на знаменатель, получим сумму двух табличных интегралов:

Пример 12. Найти интеграл:

Решение. В соответствие с формулой , преобразуем знаменатель, а затем, разделив почленно числитель на знаменатель, сведем данный интеграл к сумме двух табличных интегралов: