2.2. Интегральные модели устойчивости электрической дуги

Многие формы электрических разрядов не подчиняются закону Ома и поэтому обладают нелинейной ВАХ. При этом может оказаться, что увеличение силы тока через проводник сопровождается уменьшением напряжения на нем, т.е. ВАХ (рис. 2.1) имеет падающий участок ( S -типа).

Рисунок 2.1- Вольт-амперная характеристика S –типа

Участок цепи с такой характеристикой содержит последовательно включенные электрическую дугу и постоянное сопротивление, определяемое

отношением напряжения между концами проводника к силе тока в нем, т.е. U/i . В случае нелинейной ВАХ можно рассматривать каждый

дый малый её участок как отрезок прямой линии и ввести дифферен-

циальное сопротивление в данной точке характеристики

Если характеристика имеет падающий участок, то на этом участке 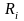отрицательно. Каждая точка ВАХ соответствует определенному состоя­нию электрического разряда, а вся кривая изображает совокупность возможных состояний разряда в данном проводнике. При отрицательном дифференциальном сопротивлении может оказаться, что не все эти состояния разряда можно получить в действительности.

Рассмотрим простую цепь (рис. 2.2), содержащую проводник с отрицательным дифференциальным сопротивлением и источник тока с ЭДС Ɛ .

Рисунок 2.2 -Схема питания электрического разряда

Обозначим через r сопротивление всей остальной частиц цепи, через i -ток в цепи и через U -напряжение на про­воднике. Тогда, согласно закону Ома, для участка цепи с ЭДС дуга моделируется уравнением:

U= Ɛ –ir (2.16)

С другой стороны U и i связаны функцией U=f(i) зависящей от свойств проводника. Поэтому при данных Ɛ и r в про­воднике окажутся возможными только те состояния разряда, при кото­рых U и i одновременно удовлетворяют обоим уравнениям. Нахожде­ние возможных состояний разряда удобно производить графически.

Для этого на графике (рис. 2.1.) проведем прямую (линия, нагрузки) согласно уравнению (2.16). Она отсекает на оси U отрезок, рав­ный Ɛ источника и наклонена к оси i на угол α=arctg r. Возможные при этих условиях состояния разряда будут определяться точками пересечения характеристики и линии нагрузки. Положим, что состояние разряда характеризуется точкой а . Если теперь увеличивать Ɛ , то линия нагрузки будет перемещаться вверх, ос­таваясь параллельной самой себе, и разряд будет плавно менять своё состояние в соответствии с участком аб . При дальнейшем увеличении Ɛ разряд скачком перейдет в состояние в , нап­ряжение на проводнике уменьшится, а сила тока увеличится. Для поддержания напряжения, соответствующего положению точки б , необходимо дальнейшее увеличение Ɛ (ветвь вг). Если исходить из правой ветви характеристики, например из точки г , и посте­пенно уменьшать Ɛ , то состояние разряда будет изменяться по гве. При этом будут существовать и состояния разряда, соответ­ствующие отрезку ве , которые невозможно было получить при уве­личении Ɛ . В момент достижения точки е произойдет скачкооб­разное изменение разряда, и он перейдет в новое устойчивое сос­тояние а . Для сохранения напряжения таким, каким оно было в точке е , необходимо уменьшить ε источника, отчего скачок то­ка еще увеличится.

Таким образом, при некотором значении напряжения, разном при прямом и обратном ходе, ток скачком изменяет свою величину. Для обеспечения устойчивости по току нужно, чтобы линия нагруз­ки при любой Ɛ пересекла ВАХ только один раз, что соответст­вует пунктирной линии на рисунке 2.1, т.е. внешнее сопротивление r должно быть больше абсолютного значения дифференциального сопро­тивления R_i в любой точке характеристики:

r>|R_i| (S-тип) (2.17)

Наряду с характеристиками S-типа существуют и характеристики N -типа. Примером проводника с характеристикой N -типа мо­жет служить туннельный полупроводниковый диод. Для устойчивости разряда в этом случае необходимо, чтобы выполнялось условие:

r< |R_i | (N -тип) (2.18)

В схеме, приведенной на рис. 2.2, отсутствуют такие парамет­ры, как емкость и индуктивность цепи. Поэтому формулы (2.17) и (2.18) выражают условие устойчивости дуги постоянного тока, кото­рое является необходимым, но может оказаться недостаточным для то­го, чтобы разряд в данном состоянии был устойчивым /59,60/. Поэто­му при случайных малых изменениях тока и напряжения в цепи должны возникать такие процессы, которые препятствовали бы этим изменени­ям.

Рассмотрим электрическую цепь (рис. 2.3), содержащую источник постоянной ε , нагрузочное сопротивление r (включающее и внут­реннее сопротивление источника), емкость С ,индуктивность L и проводник R_i с нелинейной ВАХ U=f(i)

Рисунок 2.3- Принципиальная схема питания электрической дуги

Выберем положительные направления токов так, как показано на рис. 2.3. и применим к данной цепи правила Кирхгоффа. Тогда для кон­тура ƐСrƐ

rI=-U+Ɛ, (2.19)

где U - напряжение на конденсаторе; а для контура СRLC

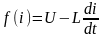(2.20)

Кроме того, имеем систему уравнений:

где q мгновенное значение заряда конденсатора.

Поскольку

то из и получаем дифференциальные уравнения первого порядка относительно i и U:

(2.21)

(2.22)

Уравнения (2.21) и (2.22) не линейны, так для проводников не подчиняющихся закону Ома, функция f(i) не линейна. В стационарном состоянии разряда

поэтому i₀ и U₀ определяются соотношениями рассмотренными ранее

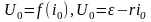(2.23)

Для выяснения, является ли состояние разряда (2.23) устойчивым, воспользуемся методом Ляпунова, а именно, предложим, что стационарные значения тока и напряжения измени­лись на малые величины х и у :

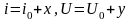
При малых изменениях тока и напряжения малый участок ВАХ можно заменить отрезком прямой линии и положить, что

Подставим полученное равенство в. (2.21) и (2.22) и, принимая во внимание условия стационарности (2.23), получим линейные уравне­ния:

(2.24)

Исключим из (2.24) y, получим линейное дифференциальное уравнение второго порядка:

(2.25)

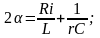
где (2.26)

Аналогичное уравнение получается и для у . Уравнение (2.25) при ω₀² > α² описывает затухающие колебания с коэффициентом затухания α. При ω₀² < α² получается апериодический процесс:

, (2.27)

где 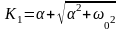(2.28)

Для того, чтобы случайные отклонения x и y затухали с течени­ем времени, т.е. состояние разряда было устойчивым, необходимо, чтобы α>0 при (ω₀² > α² ), или К₁ и К₂ >0 ( при ω₀² < α²). Если хотя бы од­на из величин К₁ или К₂ будет отрицательной, то случайные изменения тока и напряжения нарастают с течением времени, и сос­тояние разряда становится неустойчивым.

При R_i>0 все величины в (2.26) положительные_; α >0, ω₀² >0, α > , следовательно , К₁ и К₂ также положительные. От­сюда видно, что в проводниках с положительным дифференциальным сопротивлением стационарные состояния разряда всегда устойчивые.

Положим теперь, что R_i<0 тогда :

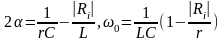(2.29)

Для того, чтобы и в этом случае К₁ и К₂ были положитель­ными, необходимо, чтобы α>0 и ω₀² > α² , а условия устойчивости:

(2.30)

Если в схеме (рис. 2.3) имеется электрическая дуга (или дру­гой проводник с характеристикой S -типа), то условие r> Ri выражает следующее: при любой Ɛ имеется только одно стационар­ное состояние разряда без скачков по току. Если в цепи выполняет­ся условие L> rC , то все состояние разряда будут устойчи­вые и можно получить всю ВАХ. При выполнении первого и нарушении второго условий (2.30) цепь, содержащая дугу, будет самовозбуждаться, и в ней установятся незатухающие колебания.

Таким образом, в разделе 2 решения могут быть использованы в качестве алгоритмов расчета устойчивости системы ИП-плазмотрон для выбранной математической модели дуги.