1 Общие сведения о булевых функциях
1.1 Частично определенные булевы функции
Логическая функция — это сложное высказывание, состоящее из нескольких простых, связанных между собой соединительными союзами. Она записывается аналитически в виде Y = f(x1,x2, ..., xn), где хi— двоичная переменная, хi { 0,1}; Y{0,1 }.
Частично определенная функция – это логическая функция, значения которой определены не на всех входных наборах. На тех входных наборах, где функция не определена, проставляется прочерк (или любой другой символ, отличный от 0 и 1) [2].
В реальных задачах очень часто бывает так, что значение булевой функции на некоторых наборах не определено и может доопределяться произвольно. В этом случае доопределение функции было бы целесообразно производить таким образом, чтобы ее минимальная нормальная форма имела наименьшее число букв из всех возможных вариантов доопределения.
Алгоритм поиска минимальной дизъюнктивной нормальной формы (ДНФ) частично определенной функции f можно представить следующим образом:
найти любым известным способом сокращенную ДНФ функции, получающейся доопределением единицами исходной функции f на всех неопределенных наборах;
выбрать минимальную ДНФ по импликантной матрице, где в столбцах выписаны лишь те конституенты единицы функции f, которые соответствуют полностью определенным единичным наборам.
Аналогичный алгоритм (с доопределением нулевыми наборами) может быть предложен для поиска конъюнктивной нормальной формы (КНФ). При этом доопределение таблицы истинности функции f может быть произведено по-разному для КНФ и ДНФ.
1.2 Методы формирования полинома Жегалкина
Известно, что любую булеву функцию можно представить полиномом Жегалкина (полиномом по модулю 2), и это представление с точностью до перестановки слагаемых единственно. Приведем некоторые наиболее известные способы построения такого полинома [3].
1.2.1 Преобразование произвольной формулы алгебры логики
Метод преобразования произвольной формулы алгебры логики состоит в следующем: сначала строим ДНФ или КНФ БФ, а затем формируем полином Жегалкина, используя известные соотношения
.
Продемонстрируем
данный метод построения полинома
Жегалкина на примере, пусть булева
функция имеет вид
.
Преобразуем
логическую
формулу
:
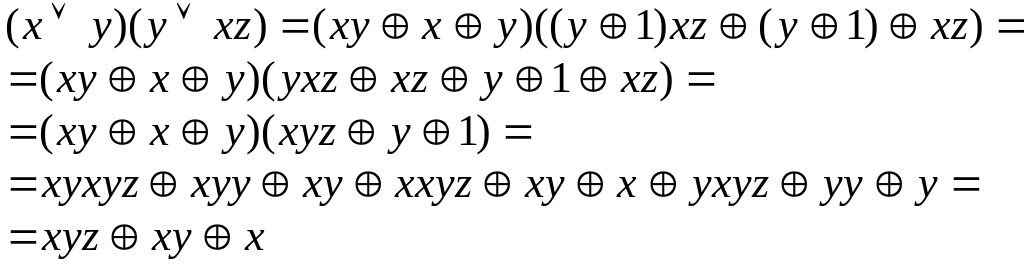
Таким
образом,
полином
Жегалкина
для
данной
функции
имеет
вид
.
1.2.2 Метод неопределенных коэффициентов
Метод неопределенных коэффициентов состоит в следующем [4]: записываем булеву функцию в виде полинома Жегалкина с неопределенными коэффициентами. Приравниваем значения функции к значениям полинома на соответствующих наборах переменных и находим неизвестные коэффициенты. На значениях исходной функции строим треугольник Паскаля, складывая каждый раз соответствующие значения функции по модулю 2. Тогда числа на левой стороне полученного треугольника определяют коэффициенты полинома Жегалкина при монотонных конъюнкциях, соответствующих наборам переменных. Напомним, что элементарная конъюнкция называется монотонной, если она не содержит отрицаний переменных. Константа 1 (т. е. элементарная конъюнкция нулевого ранга) считается по определению монотонной конъюнкцией.
Теперь воспользуемся методом неопределенных коэффициентов. Для этого запишем нашу функцию в виде многочлена с неопределенными коэффициентами:
,
где A, B, C, D, E, F, G, H ∈{0,1}.
Таблица истинности нашей функции выглядит следующим образом:
Таблица 1.1 – Таблица истинности функции
x |
y |
z |
x∨y |
y |
xz |
y∨xz |
(x∨y)(y∨xz) |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
Чтобы определить неизвестные коэффициенты, подставим соответствующие значения переменных в правую и левую части формулы и получим систему:
Решая систему, получим коэффициенты равные: H=0, G=0, F=0, D=0, E=1, C=0, B=1, A=1. Подставляя найденные значения A, B, C, D, E, F, G, H в формулу
,
получим
полином Жегалкина того же вида, что и
методом преобразования произвольной
формулы алгебры логики:
.