Экзаменационные вопросы по математике для студентов 1 курса очного отделения фак. Бхф спец. «Биология»

1. Матрицы. Основные понятия.

Матрицей называется прямоугольная таблица чисел, содержа­щая т строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде

или сокращенно, А=(а_ij), где i= l, m(т.е. i=1,2,3,…,m)- номер строки, i= l,n(т.е. i= 1,2,3,…,n) –номер столбца. Матрицу А называют матрицей размера m_*n и пишут Аm_*n _*Числа a_ij, составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из левого верхнего угла, образуют главную диагональ матрицы. Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е. А= В, если a_ij = b_ij, где i = l,m, j = l,n.

2. Классификация матриц: квадратная, диагональная и т.Д.

Транспонирование матрицы. Примеры.

Матрица, у которой число строк равно числу столбцов, назы­вается квадратной. Квадратную матрицу размера п х п называют матрицей n-го порядка. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е. Так, единичная матрица 3-го порядка имеет вид

Квадратная матрица называется треугольной, если все элемен­ты, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нуле­вой. Обозначается буквой О. Имеет вид

В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике. Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка, соответственно). Их вид:

Матрица, полученная из данной заменой каждой ее строки столб­цом с тем же номером, называется матрицей транспонированной к данной. Обозначается А^т. Так если А^т =(1 0)

3. Матрицы. Действия над матрицами Примеры.

Операция сложения матриц вводится только для матриц одина­ковых размеров. Например,

+ =

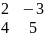Аналогично определяется разность матриц.

Произведением матрицы А_т*п — (а_ij) на число k

Матрица -A = (-1) * А называется противоположной матри­це А.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

4. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду. Примеры.

Элементарными преобразованиями матрицы называются следующие ее преобразования: I. Перестановка двух столбцов (строк) матрицы. II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля. III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.

5. Невырожденные матрицы. Обратная матрица. Примеры.

Матрица А^-1 наз. обратной для матрицы А , если А^-1 А = Е Теорема. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е.  А 0. Элемент обратной матрицы ( А^-1)_i j равен алгебраическому дополнению A_j i матрицы А , деленному на det A : ( A^-1)_i j = A_j i / det A(индексы поменяли места) или A^-1 = (detA)^-1 ||A_ij||^T Пример: Построить матрицу обратную к данной. 3 -1 -1 det^ A=52

А= 2 2 4 A₁₁=14 A₁₂ =-6 A₁₃ =-4 A₂₁ =4 A₂₂ =2 A₂₃ =10

-1 -3 1 A₃₁ =-2 A₃₂ =-14 A₃₃ =8

Составим из них присоединённую матрицу  и транспонируем ее и вычислим по формуле A^–1 = (detA)^–1||A_ij||^T . И после вычислим произведение. Получилась единичная матрица.