
- •Введение
- •1. Обыкновенные дроби и дробные выражения
- •Действия с обыкновенными дробями:
- •1.1 Контрольные вопросы и задания для самостоятельного решения по разделу 1
- •2. Проценты
- •2.1 Контрольные вопросы и задания для самостоятельного решения по разделу 2
- •3. Степени и корни
- •3.1 Контрольные вопросы и задания для самостоятельного решения по разделу 3
- •4. Уравнения и методы их решения
- •4.1 Контрольные вопросы и задания для самостоятельного решения по разделу 4
- •5 Логарифмы.
- •5.1 Контрольные вопросы и задания для самостоятельного решения по разделу 5
- •6. Простейшие задачи по теории вероятностей
- •6.1 Контрольные вопросы и задания для самостоятельного решения по разделу 6
- •7. Простейшие тригонометрические уравнения
- •7.1 Контрольные вопросы и задания для самостоятельного решения по разделу 7
- •8. Производные элементарных функций
- •8.1 Контрольные вопросы и задания для самостоятельного решения по разделу 8
- •9. Площадь криволинейной трапеции
- •9.1 Контрольные вопросы и задания для самостоятельного решения
- •Литература и интернет ресурсы
7.1 Контрольные вопросы и задания для самостоятельного решения по разделу 7
Ответьте на вопросы:
Какое уравнение называется тригонометрическим?
Какое уравнение называется однородным первой степени?
Какое уравнение называется однородным второй степени?
Решите упражнения:
1)  2)
2) 
3)  4)
4) 
5) 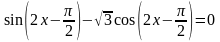
6) 
7)
8) 
9) 
10) 
11) 
12)  13)
13) 
14) 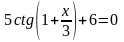 15)
15) 
16)  17)
17) 
18)  19)
19) 
Проверьте своё решение:
Ответы:
1)
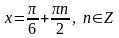 2)
2) 
3)  4)
4) 
5)
6) 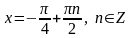
7) 8)
9)  10)
10) 
11)
12) 
13) 
14) 
15) 
16) 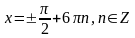 17)
17) 
18) 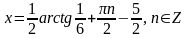
19) 
8. Производные элементарных функций
В данной таблице приведены производные основных элементарных функций и правила дифференцирования, которые нужно очень хорошо выучить, чтобы применять к решению примеров:

Например:
Найдите производную данной функции:
1) 
2) 
3) 
4) 
5) 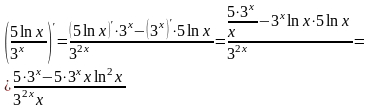
6) 
7) 
8) 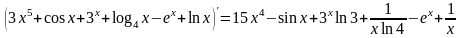
Элементы исследования функции с помощью производной
Производные применяют для исследования графиков функций:
устанавливают промежутки монотонности; точки экстремума; наибольшее и наименьшее значения функции на отрезке.
Функцией называется правило f, по которому каждому элементу х множества Х ставится в соответствие единственный элемент у множества У.
План исследования функций:
Область определения
Множество значений
Четность, не четность
Непрерывность
Нули функции
Промежутки знакопостоянства
Промежутки монотонности
Критические точки
Точки экстремума
Экстремум функции
Наибольшее и наименьшее значение функции
Чтобы исследовать функцию полезно найти её производную и приравнять её к нулю. Тем самым найдём стационарные точки. Затем исследуем промежутки в окрестности стационарных точек:
если производная положительна, то функция возрастает;
если производная отрицательна, то функция убывает.
Стационарные точки становятся точками экстремума, если производная меняет знак: с «+» на «» точка max; с «» на «+» точка min

Например:

Используя эту подготовительную работу можно строить график.
Необходимо ещё найти значение функции в стационарных точках, и добавить дополнительные точки для более точного построения.
ПРИМЕР 1


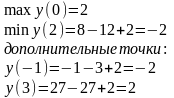


ПРИМЕР 2
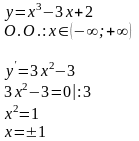



ПРИМЕР 3




ПРИМЕР 4
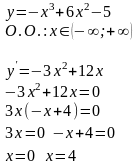



8.1 Контрольные вопросы и задания для самостоятельного решения по разделу 8
Ответьте на вопросы:
Как найти производную степенной функции?
Как найти стационарные точки?
Что такое точки экстремума?
Как найти промежутки монотонности функции?
Решите упражнения:
№ 1 Найти производную функции: № 2 Постройте график функции:
1)  1)
1)

2) 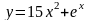 2)
2) 
3) 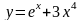 3)
3) 
4)  4)
4) 
5)  5)
5) 
6)  6)
6) 
Проверьте своё решение:
Ответы:
№ 1
1)  2)
2)
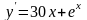
3)  4)
4) 
5)  6)
6) 
№ 2
1)

2)
3)
4)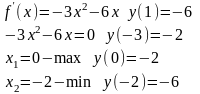
5)
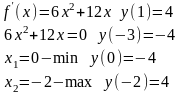
6)
9. Площадь криволинейной трапеции
Что такое «криволинейная трапеция»?
Фигура,
ограниченная функцией
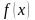 прямыми х
= а , х = b
и осью Ох
называется криволинейной трапецией.
прямыми х
= а , х = b
и осью Ох
называется криволинейной трапецией.
Вычисляется площадь по формуле Ньютона-Лейбница:

Число a называется нижним пределом интегрирования, а число b верхним пределом интегрирования.
Криволинейная трапеция может быть различного вида:
I.Стандартная криволинейная трапеция:
(нижнее основание – ось Ох, верхнее основание функция f(x)).

II. Трапеция, расположенная «вверх ногами»:
(верхнее основание – ось Ох, нижнее основание функция f(x)).


III. Трапеция, состоящая из отдельных частей
(частей может быть больше двух):
(нижнее основание – ось Ох, верхних оснований несколько, т.е. функции h(x) и g(x) являются верхними основаниями каждая над своей частью).


 IV.
Трапеция, находящаяся между функциями:
IV.
Трапеция, находящаяся между функциями:
(верхнее основание функция g(x), нижнее основание функция h(x)).

И так, криволинейные трапеции делятся на 4 типа:

Но для интегрирования функций полезно вспомнить основные формулы интегрирования:
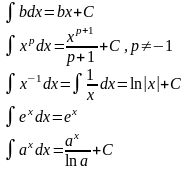

Чаще всего в заданиях на вычисление площади встречается квадратичная функция и возникает потребность построения обычной параболы:


Например:

Пример 1. Вычислить площадь фигуры, ограниченной графиками функций
y=x2 – 2x+2 и y=2+6x – x2.
 Решение.
Решение.
1) Выполняем чертеж;
2) Найдем пределы интегрирования:
x2–2x+2=2+6x–x2,
откуда х=0 – нижний предел интегрирования
и х=4 – верхний предел интегрирования;
3) Составим подынтегральную функцию:
f(x)=2+6x–x2 – (x2–2x+2)=8x–2x2;


Пример 3

Вычислить площадь фигуры, ограниченной линиями
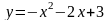
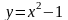 и
и


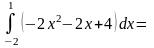



О твет: 9 кв.ед.
