3. Степени и корни

Что такое степень?

Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а.

Степень с основанием а и показателем n записывается так: аⁿ . Читается “ а в степени n ”; “ n- я степень числа а ”.

По определению степени:

а¹ = а

а² = а•а

а³ = а•а•а

а⁴ = а• а•а•а

. . . . . . . . . . . .

аⁿ =

Например:

3³ = 3• 3• 3 = 27

0⁴ = 0• 0• 0• 0 = 0

( -5 )³ = ( -5 ) • ( -5 ) • ( -5 ) = -125

7¹ = 7

При умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают:

a^maⁿ = a^{m + n} .

a^maⁿa^k = a^{m + n}a^k = a^{( m + n ) + k} = a^{m + n + k}

При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя:

a^m : aⁿ = a^{m - n}

аⁿ : aⁿ = 1, т.е. а⁰ = 1

При возведении в степень произведения возводят в эту степень каждый множитель и результат перемножают:

( ab )ⁿ = aⁿ•bⁿ

( a• b• c )ⁿ = aⁿ •bⁿ •cⁿ ;

( a• b• c• d )ⁿ = aⁿ •bⁿ •cⁿ •dⁿ .

При возведении степени в степень основание оставляют тем же, а показатели перемножают:

( а^m )ⁿ = а^{m n}

Что такое квадратный корень?

Это понятие очень простое. Математики на каждое действие стараются найти противодействие. Есть сложение - есть и вычитание. Есть умножение - есть и деление. Есть возведение в квадрат... Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня) в математике обозначается вот таким значком:

Сам значок называется "радикал".

Как извлечь корень квадратный из 9? Нужно просто сообразить: какое число в квадрате даст нам 9? Да конечно же 3! Значит:

Например:

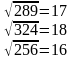
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.

Выражение, в котором под знаком квадратного корня стоит отрицательное число - не имеет смысла! Это запретная операция. Такая же запретная, как и деление на ноль. Квадратные корни (и корни чётных степеней) из отрицательных чисел извлечь нельзя!

Важно помнить, что радикалы -- это дробный показатель степени:

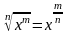
Например:

3.1 Контрольные вопросы и задания для самостоятельного решения по разделу 3

Ответьте на вопросы:

1. Что такое степень?

2. Перечислите свойства степеней.

3. Как записать дробный показатель степени в виде радикала?

Решите упражнения:

1. Упростите выражение

2. Вычислите:

3. Упростите выражение:

_4. Вычислите: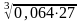

5. Упростите выражение

6. Найдите значение выражения при

7. Представьте выражение

в виде степени с основанием а

8. Упростите выражение

9. Вычислите

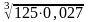
10. Упростите выражение:

11. Найдите значение выражения:

12. Представьте в виде степени выражение:

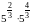
Проверьте своё решение:

Ответы:

1) 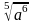2) 10 3) 4) 1,2

5 ) 5b² 6) 2 7) а³ 8) 2,4

9) 1,5 10) 9m⁷ 11) 36 12) 25

4. Уравнения и методы их решения

Основные понятия:

Одним из важнейших умений в математике – это умение решать квадратные уравнения.

Алгоритм решения квадратного уравнения по формуле корней:

1) Найти число, называемое дискриминантом квадратного уравнения

и равное D = b²- 4ac.

2) Дискриминант показывает сколько корней имеет уравнение

1. если D<0, то данное квадратное уравнение не имеет корней;

2. е сли D=0, то данное квадратное уравнение имеет единственный корень, который равен

3. если D>0, то данное квадратное уравнение имеет два корня, которые равны

Например:

Умение удачно ввести новую переменную – облегчает решение:

Дробно-рациональные уравнения

Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе.

ОДЗ – (Область Допустимых Значений).

Это те значения икса, которые могут быть в принципе. Т.к. делить на ноль нельзя, знаменатели в дробно-рациональных уравнениях не должны равняться нулю. Перед решением внимательно исследуйте пример и определите ОДЗ. Все найденные в процессе решения корни нужно проверять: не обратят ли они какой-либо из знаменателей в ноль (такой корень будет посторонним и в окончательный ответ не попадёт).