5.4. Циклічні коди

Циклічні коди названі так тому, що в них частина комбінацій коди або всі комбінації можуть бути отримані шляхом циклічного зрушення однієї або декількох комбінацій коди. Циклічне зрушення здійснюється справа наліво, причому крайній лівий символ кожного разу переноситься в кінець комбінації. Циклічні коди, практично¹¹, всі відносяться до систематичних кодів, в них контрольні і інформаційні розряди розташовані на строго певних місцях. Крім того, циклічні коди належать до блокових код. Кожен блок (одна буква є окремим випадком блоку) кодується самостійно.

Ідея побудови циклічних код базується на використанні двійкових чисел многочленів, що не приводяться в полі. ¹²Не приводяться називаються многочлени, які не можуть бути представлені у вигляді твору многочленів нижчих ступенів з коефіцієнтами з того ж поля, так само, як прості числа не можуть бути представлені твором інших чисел. Іншими словами, многочлени, що не приводяться, діляться без залишку тільки на себе або на одиницю.

Многочлени, що не приводяться, в теорії циклічних код грають роль створюючих (генераторних, таких, що проводять) многочленів. Якщо задану кодову комбінацію помножити на вибраний многочлен, що не приводиться, то отримаємо циклічний код, що коректують здібності якого визначаються многочленом, що не приводиться.

Припустимо, потрібний закодувати одну з комбінацій чотиризначного двійкового коду. Припустимо також, що ця комбінація - . Поки не обгрунтовувавши свій вибір, беремо з таблиці многочленів, що не приводяться, як створюючий многочлен . Потім помножимо на одночлен того ж ступеня, що і створюючий многочлен. Від множення многочлена на одночлен ступеня п ступінь кожного члена многочлена підвищиться на що еквівалентно приписуванню нулів з боку молодших розрядів многочлена. Оскільки ступінь вибраного многочлена, що не приводиться, рівний трем, то початкова інформаційна комбінація умножається на одночлен третього ступеня:

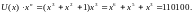
Це робіться|чинить| для того, щоб згодом на місці цих нулів|нуль-індикаторів| можна було б записати розряди, що коректують.

Значення розрядів, що коректують, знаходять|находять| по результату від ділення|поділу| на :

або

Таким чином

або в загальному|спільному| вигляді|виді|

(59)

де - приватне, а - залишок від ділення на .

Оскільки в двійковій арифметиці а значить то можна при складанні двійкових чисел переносити складову з однієї частини рівність в іншу без зміни знаку (якщо це зручно), тому рівність вигляду можна записати і як і як . Вся три рівність в даному випадку означають, що або і рівні 0, або а і рівні 1, тобто мають однакову парність.

Таким чином, вираз|вираження| (59) можна записати як

(60)

що у разі|в разі| нашого прикладу|зразка| дасть

або

Многочлен 1101001 і є шукана комбінація, де 1101 - інформаційна частина|частка|, а 001 - контрольні символи. Відмітимо|помітимо|, що шукану комбінацію ми отримали|одержували| б і як в результаті|унаслідок| множення однієї з комбінацій повної|цілковитої| чотиризначної двійкової коди (в даному випадку 1111) на створюючий многочлен, так і множенням заданої комбінації на одночлен, що має той же ступінь|міру|, що і вибраний створюючий многочлен (у нашому випадку таким чином була отримана|одержувати| комбінація 1101000) з|із| подальшим|наступним| додаванням|добавляти| до отриманого|одержувати| твору|добутку| залишку|остачі| від ділення|поділу| цього твору|добутку| на створюючий многочлен (у нашому прикладі|зразку| залишок|остача| мав вигляд|вид| 001).

Таким чином, ми вже знаємо два способи утворення комбінацій лінійних систематичних код, до яких відносяться і що цікавлять нас циклічні коди. Ці способи з'явилися теоретичною підставою|основою| для побудови|шикування| кодуючих і декодуючих пристроїв|устроїв|.

Шифратори циклічних код, в тому або іншому вигляді|виді|, побудовані|спорудити| за принципом множення двійкових многочленів. Кодові комбінації виходять в результаті|унаслідок| складання сусідніх комбінацій по модулю два, що, як ми побачимо нижче, еквівалентно множенню першої комбінації на двочлен .

Отже, комбінації циклічних код можна представляти у вигляді многочленів, у яких показники ступеня відповідають номерам розрядів, коефіцієнти при х дорівнюють 0 або 1 залежно від того, стоїть 0 або 1 в розряді кодової комбінації, яку представляє даний многочлен. Наприклад

Циклічне зрушення кодової комбінації аналогічне множенню відповідного многочлена на х:

Якщо ступінь многочлена досягає розрядності коди, то відбувається «перенесення» в нульовий ступінь при . У шифраторах циклічних код ця операція здійснюється шляхом з'єднання виходу осередку старшого розряду з входом осередку нульового розряду. Складання по модулю 2 будь-яких двох сусідніх комбінацій циклічної коди еквівалентно операції множення многочлена відповідного комбінації першого доданку на многочлен якщо приведення подібних членів здійснюється по модулю 2:

тобто існує принципова можливість|спроможність| отримання|здобуття| будь-якої кодової комбінації циклічної коди шляхом множення відповідним чином підібраного створюючого многочлена на деякий інший многочлен.

Проте мало побудувати циклічний код. Треба уміти виділити з нього можливі помилкові розряди, тобто ввести деякі пізнавачі помилок, які виділяли б помилковий блок зі всіх інших. Оскільки циклічні коди - блокові, то кожен блок повинен мати свій пізнавач. І тут вирішальну роль грають властивості створюючого многочлена . Методика побудови циклічної коди така, що створюючий многочлен бере участь в утворенні кожної кодової комбінації, тому будь-який многочлен циклічної коди ділиться на створюючий без залишку. Але без залишку діляться тільки ті многочлени, які належать даному коду, тобто створюючий многочлен дозволяє вибрати дозволені комбінації зі всіх можливих. Якщо ж при діленні циклічної коди на створюючий многочлен буде отриманий залишок, то означає або в коді відбулася помилка, або це комбінація якогось іншої коди (заборонена комбінація), що для декодуючого пристрою не має принципової різниці. По залишку і виявляється наявність забороненої комбінації, тобто виявляється помилка. Залишки від ділення многочленів є пізнавачами помилок циклічних кодів.

З іншого боку, залишки від ділення|поділу| одиниці з|із| нулями|нуль-індикаторами| на створюючий многочлен використовуються для побудови|шикування| циклічних код (можливість|спроможність| цього видно|показний| з|із| виразу|вираження| (60)).

При діленні|поділі| одиниці з|із| нулями|нуль-індикаторами| на створюючий многочлен слід пам'ятати, що довжина залишку|остачі| має бути не менше числа контрольних розрядів, тому у разі|в разі| браку|нестачі| розрядів в залишку|остачі| до залишку|остачі| приписують справа необхідне число нулів|нуль-індикаторів|. Наприклад

починаючи|розпочинати| з|із| восьмого, залишки повторюватимуться.

Залишки від ділення використовують для побудови створюючих матриць, які, завдяки своїй наочності і зручності отримання похідних комбінацій, набули широкого поширення для побудови циклічних код. Побудова створюючої матриці зводиться до складання одиничної транспонованої і додаткової матриці, елементами якої є залишки від ділення одиниці з нулями на створюючий многочлен . Нагадаємо, що одинична транспонована матриця є квадратною матрицею, всі елементи якої - нулі, окрім елементів, розташованих по діагоналі справа наліво зверху вниз (у нетранспонованій матриці діагональ з одиничними елементами розташована зліва направо зверху вниз). Елементи додаткової матриці приписуються праворуч від одиничної транспонованої матриці.

Проте|однак| не всі залишки від ділення|поділу| одиниці з|із| нулями|нуль-індикаторами| на створюючий многочлен можуть бути використані як елементи додаткової матриці. Використовуватися можуть лише ті залишки, вага яких де - мінімальна кодова відстань. Довжина залишків має бути не менше кількості контрольних розрядів, а число залишків повинне дорівнювати числу інформаційних розрядів.

Рядками створюючої матриці є перші комбінації шуканої коди. Решта комбінацій коди виходить в результаті підсумовування по модулю 2 всіляких поєднань рядків створюючої матриці¹³.

Описаний вище метод побудови|шикування| створюючих матриць не є|з'являється| єдиним. Матриця твірної може бути побудована|спорудити| в результаті|унаслідок| безпосереднього множення елементів одиничної|поодинокої| матриці на створюючий многочлен. Це часто буває зручнішим, ніж знаходження залишків від ділення|поділу|. Отримані|одержувати| коди нічим не відрізняються від код, побудованих|спорудити| по створюючих матрицях, в яких додаткова матриця складається із залишків від ділення|поділу| одиниці з|із| нулями|нуль-індикаторами| на створюючий многочлен.

Матриця твірної може бути побудована|спорудити| також шляхом циклічного зрушення|зсуву| комбінації, отриманої|одержувати| в результаті|унаслідок| множення рядка одиничної|поодинокої| матриці рангу на створюючий многочлен.

На закінчення пропонуємо ще один метод побудови|шикування| циклічних код. Гідністю|чеснотою| цього методу є|з'являється| виняткова простота схемних реалізації кодуючих і декодуючих пристроїв|устроїв|.

Для отримання|здобуття| комбінацій циклічної коди в цьому випадку досить провести циклічне зрушення|зсув| рядка створюючої матриці і комбінації, що є|з'являється| її дзеркальним відображенням. При побудові|шикуванні| код з|із|,, число комбінацій, що отримуються|одержують| підсумовуванням по модулю 2 всіляких поєднань рядків створюючої матриці, дорівнює числу комбінацій, що отримуються|одержують| в результаті|унаслідок| циклічного зрушення|зсуву| рядка створюючої матриці і дзеркальної нею комбінації. Проте|однак| цей спосіб використовується для отримання|здобуття| код з|із| малим числом інформаційних розрядів. Вже при число комбінацій, що отримуються|одержують| в результаті|унаслідок| циклічного зрушення|зсуву|, буде менше, ніж число комбінацій, що отримуються|одержують| в результаті|унаслідок| підсумовування всіляких поєднань рядків створюючої матриці.

Число ненульових комбінацій, що отримуються|одержують| в результаті|унаслідок| підсумовування по модулю 2 всіляких поєднань рядків створюючої матриці

(61)

де - число інформаційних розрядів коди¹⁴.

Число ненульових комбінацій, що отримуються|одержують| в результаті|унаслідок| циклічного зрушення|зсуву| будь-якого рядка створюючої матриці і дзеркальної нею комбінації

(62)

де - довжина кодової комбінації.

При числі інформаційних розрядів число комбінацій від підсумовування рядків створюючої матриці росте|зростає| набагато швидше, ніж число комбінацій, що отримуються|одержують| в результаті|унаслідок| циклічного зрушення|зсуву| рядка створюючої матриці і дзеркальної нею комбінації. У останньому випадку коди виходять надмірними|надлишковими| (оскільки|тому що| при тій же довжині коди можна іншим способом передати|передавати| більшу кількість повідомлень), відповідно, падає відносна швидкість передачі інформації. У таких випадках доцільність застосування|вживання| того або іншого методу кодування може бути визначена з|із| конкретних технічних умов.

Помилки в циклічних кодах виявляються і виправляються за допомогою залишків від ділення отриманої комбінації на створюючий многочлен. Залишки від ділення є пізнавачами помилок, але не указують безпосередньо на місце помилки в циклічному коді.

Ідея виправлення помилок базується на тому, що помилкова комбінація після|потім| певного числа циклічних зрушень|зсувів| “ підганяється|припасовує| ” під залишок|остачу| таким чином, що в сумі із|із| залишком|остачею| вона дає виправлену комбінацію. Залишок|остача| при цьому є не що інше, як різницю між спотвореними і правильними символами, одиниці в залишку|остачі| стоять якраз на місцях|місце-милях| спотворених розрядів в підігнаній|припасовувати| циклічними зрушеннями|зсувами| комбінації. Підганяють|припасовують| спотворену комбінацію до тих пір, поки число одиниць в залишку|остачі| не дорівнюватиме числу помилок в коді. При цьому, природно, число одиниць може бути або дорівнює числу помилок, що виправляються даним кодом (код виправляє 3 помилки і в спотвореній комбінації 3 помилки), або менше s (код виправляє 3 помилки, а в прийнятій комбінації - 1 помилка).

Місце|місце-миля| помилки в кодовій комбінації не має значення. Якщо те після|потім| певної кількості зрушень|зсувів| всі помилки опиняться в зоні “разової” дії створюючого многочлена, тобто досить отримати|одержувати| один залишок|остачу|, вага якого, і це вже буде досить для виправлення спотвореної комбінації. У цьому сенсі|змісті| коди БЧХ (про них ми говоритимемо нижче) можуть виправляти пачки помилок, аби довжина пачки не перевищувала s.