40. Примеры решения уравнения шредингера

40.1. Туннельный эффект

* Туннельный эффект – это прохождение микрочастицы через потенциальный барьер в том случае, когда полная энергия Е частицы меньше высоты барьера (см. рис.).

В классической теории это невозможно. Если классическая частица с энергией Е = mV²/2, скользя без трения, повстречает горку высотой h  V²/2g, то, поднявшись до точки поворота, в которой вся ее кинетическая энергия превратится в потенциальную, частица эту горку «не пройдет», повернув обратно.

И спользуемый термин «туннельный эффект» может создать неверное впечатление о точечной микрочастице, преодолевающей потенциальный барьер сквозь некий «туннель». Это не так. Квантовая теория – уравнение Шредингера – описывает не точечную частицу, а «размазанное» в пространстве «облако» плотности вероятности ее обнаружения |(x,t)|². Если часть этого «облака» оказывается позади барьера, то для микрочастицы существует конечная вероятность оказаться за барьером.

Если же рассматривать частицу как точечный объект, уменьшая неопределенность ее координаты x, то возрастает неопределенность импульса и энергии. Тогда частица может оказаться в виртуальном состоянии и изменить свою энергию на величину Е  U₀ – Е. Это происходит в результате поглощения виртуального фотона, испускаемого частицами, создающими потенциальный барьер. Налетающая частица окажется над барьером шириной а (рис.).

Е сли время существования в таком состоянии t  а/с (с – скорость света в вакууме), то она может успеть «перелететь» через барьер и вернуться в состояние с прежней энергией Е.

* Полная энергия микрочастицы Е при туннельном переходе измениться не может.

Используем соотношение неопределенностей для определения ширины потенциального барьера:

xp_x /2; yp_y /2; zp_z /2; tE /2;…

для которого возможен туннельный эффект:

Et   (U₀ –E)(a/c) или a  c /(U₀ –E).

Покажем, что уравнение Шредингера допускает туннельный эффект. Пусть частица массы m и энергией Е движется вдоль оси x и налетает на потенциальную ступеньку (область, в которой потенциальная энергия U₀ частицы постоянна, U₀  Е).

Это происходит, например, при движении свободного электрона с энергией Е в металле. Существование двойного электрического слоя на границе металла приводит к тому, что потенциальная энергия электрона вне металла возрастает на величину U₀, где U₀ – Е = А_вых – работа выхода электрона из металла. Классический электрон оказаться вне металла в области x  0 не может и вылетает из металла только за счет фотоэффекта, поглощая фотон с энергией   А_вых.

К потенциальной энергии U(x) можно добавить или вычесть любую постоянную величину (так как U определена с точностью до произвольной постоянной).  Совместим начало координат x = 0 со ступенькой и пусть в области I (x  0) потенциальная энергия падающей на ступеньку частицы равна нулю (см. рис.).

Уравнение Шредингера

в нашем случае запишется в виде:

, x  0,

, x  0,

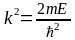
где  0,  0.

Решения этих уравнений:

_I (x) = Ae^ikx + Be^–ikx; _II(x) = Ce^–x + Fe^x, (*)

Здесь _пад = Ae^ikx_, _отр= Be^–ikx, _пр = Ce^–x, Fe^x = 0, А, В, С, F – постоянные интегрирования.

Пусть Е – U = p²/2m  в области I имеем:

k = p/ (сравним с )  _пад = Ae^ikx = Ае^–ipx/ описывает свободную частицу, летящую вдоль оси x, то есть, падающую на ступеньку.

_отр= Be^–ikx = Ве^–ipx/ соответствует частице, летящей против оси x, то есть, отраженной от ступеньки.

Волновая функция _пр = Ce^–x опишет состояние частицы, прошедшей в классически запрещенную область II (классическая частица в этой области не существует, так как ее импульс p = (2m/(E – U₀))^1/2 будет мнимым из-за

Е  U₀, см. рис.). F = 0 из граничного условия |_II|²_x  (вероятность обнаружения частицы в области x не может быть бесконечной).

Константы А, В и С ищем из условия непрерывности функции (x) на границе двух областей:

* На любой границе следует приравнять волновые функции и их первые производные:

_I|_{x = 0} = _II|_{x = 0}; (d_I/dx)|_x=0 = (d_II/dx)|_x=0  A + B = C;

ikA – ikB = – C,

откуда имеем систему уравнений: .

Вероятность обнаружения частицы в области II не равна нулю:

|_пр|² = |Ce^–x|² = = = .

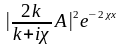Эта вероятность очень быстро убывает по экспоненте с глубиной проникновения x в классически запрещенную область и быстро становится пренебрежимо малой. Частицы не могут проникнуть глубоко и обязаны отразиться с вероятностью, равной 1.

Но если вместо бесконечной прямоугольной ступеньки рассматривать прямоугольный потенциальный барьер конечной ширины а, то частица с вероятностью |_пр|²_x=a = conste^–2x окажется за барьером и улетит далее вдоль оси x. Осуществится туннельный эффект.

Вероятность преодоления потенциального барьера:

D = j_пр/j_пад – отношение потока прошедших частиц к потоку падающих.

Для прямоугольного барьера:

D = |_пр|²/|_пад|² = conste^–2а = constexp(–2 )/

Для потенциального барьера произвольной формы:

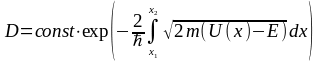– вероятность туннельного преодоления падающей микрочастицей с массой m и энергией Е потенциального барьера произвольной формы. Эта формула является приближенной (так как константа перед экспонентой не определена).